X
Код презентации скопируйте его
Решение задач по теме "Пирамида" 10 класс
Скачать эту презентацию
Презентация на тему Решение задач по теме "Пирамида" 10 класс
Скачать эту презентациюCлайд 1
УРОК-ПРАКТИКУМ В 10 КЛАССЕ Пирамида. Решение задач по теме «Пирамида». учитель математики Огурцова Алла Юрьевна
Cлайд 2
Цели урока Изучить мнемонический прием. Вывести формулы перехода основных углов в правильных пирамидах. Научиться применять мнемонический прием для доказательства зависимостей между углами в правильной пирамиде и решения задач.
Cлайд 3
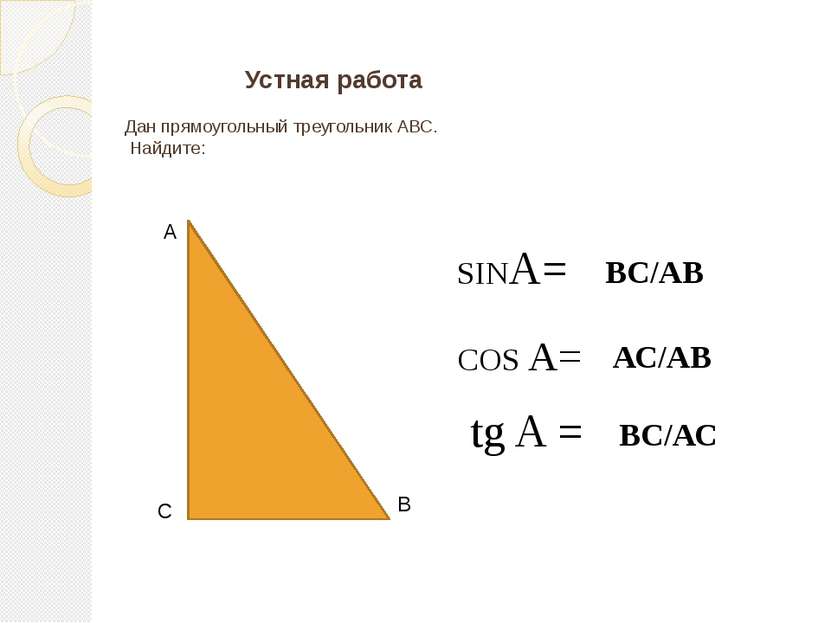
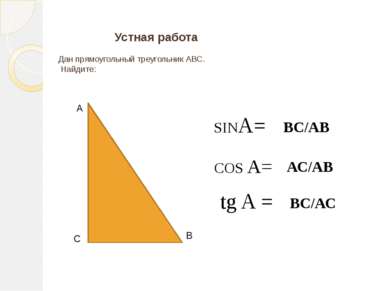А В С Устная работа Дан прямоугольный треугольник АВС. Найдите: SINA= COS A= tg A = ВС/АВ АС/АВ ВС/АС
Cлайд 4
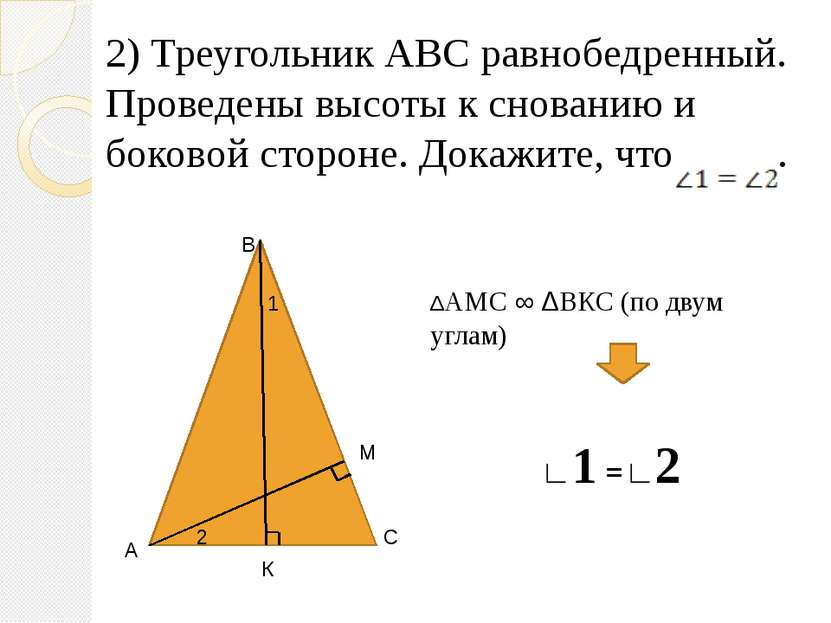
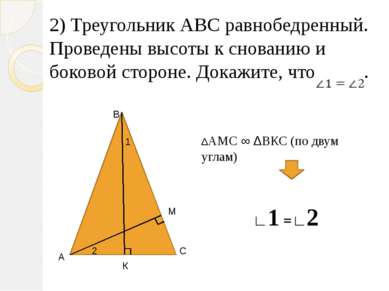2) Треугольник АВС равнобедренный. Проведены высоты к снованию и боковой стороне. Докажите, что . А В С К М 1 2 ΔАМС ∞ ΔВКС (по двум углам) ∟1 =∟2
Cлайд 5
Основные элементы пирамиды А В С D О S K
Cлайд 6
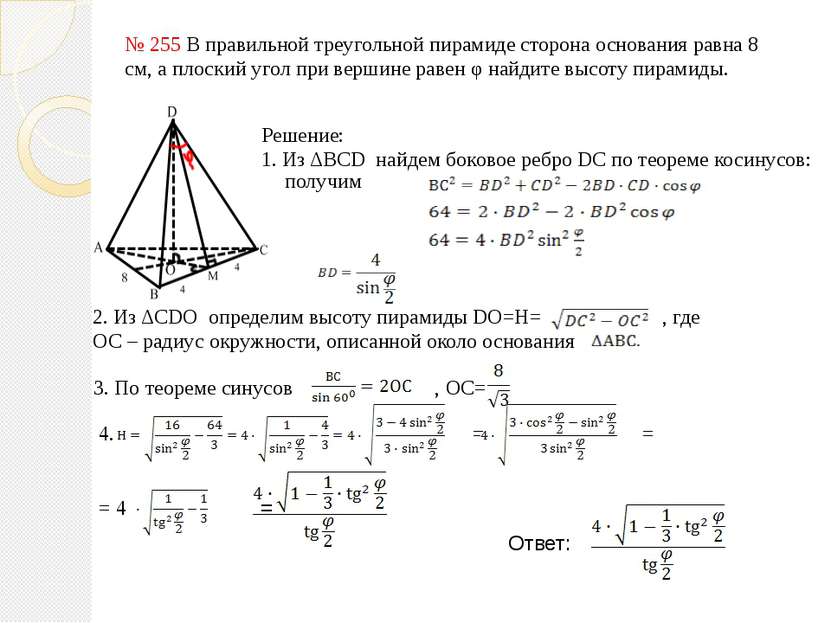
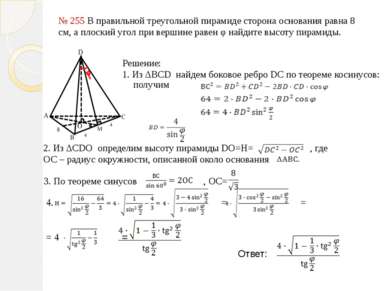№ 255 В правильной треугольной пирамиде сторона основания равна 8 см, а плоский угол при вершине равен φ найдите высоту пирамиды. Решение: 1. Из ΔBCD найдем боковое ребро DC по теореме косинусов: получим 2. Из ΔCDO определим высоту пирамиды DO=H= , где ОС – радиус окружности, описанной около основания 3. По теореме синусов , ОС= 4. = = = 4 = Ответ:
Cлайд 7
S A B O α β x
Cлайд 8
МНЕМОНИКА Три закона Ньютона: 1) не пнёшь — не полетит 2) как пнёшь, так и полетит 3) как пнёшь, так и получишь Биссектриса — это крыса (бегает по углам и делит их пополам) Медиана — это обезьяна (лазает по сторонам, делит их пополам)
Cлайд 9
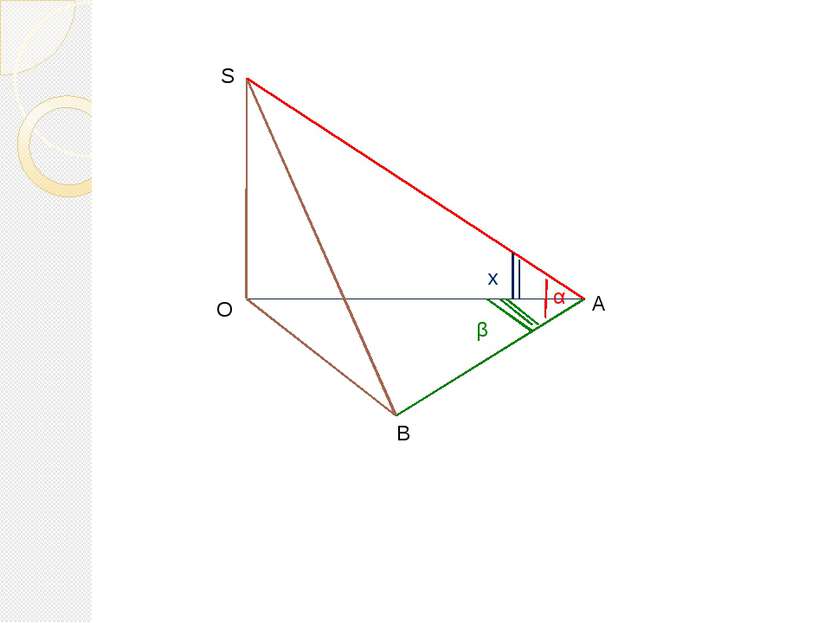
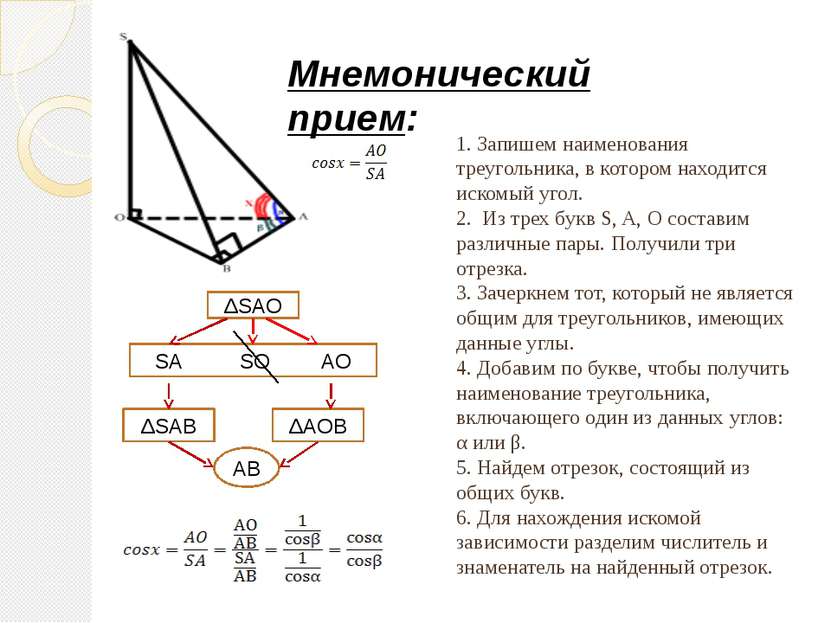
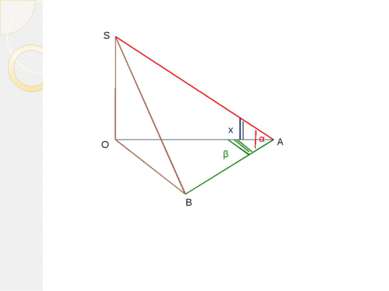
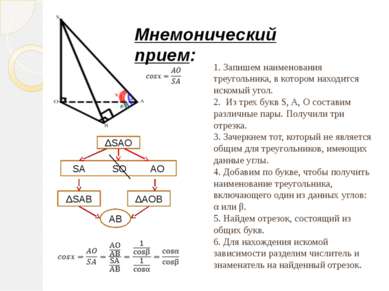1. Запишем наименования треугольника, в котором находится искомый угол. 2. Из трех букв S, A, O составим различные пары. Получили три отрезка. 3. Зачеркнем тот, который не является общим для треугольников, имеющих данные углы. 4. Добавим по букве, чтобы получить наименование треугольника, включающего один из данных углов: α или β. 5. Найдем отрезок, состоящий из общих букв. 6. Для нахождения искомой зависимости разделим числитель и знаменатель на найденный отрезок. Мнемонический прием: ΔSAO SA SO AO ΔSAB ΔAOB AB
Cлайд 10
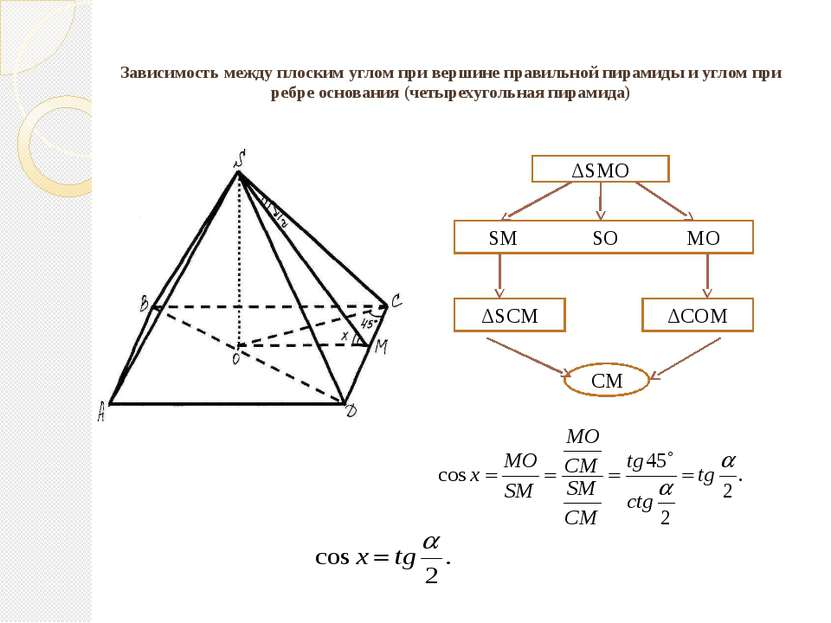
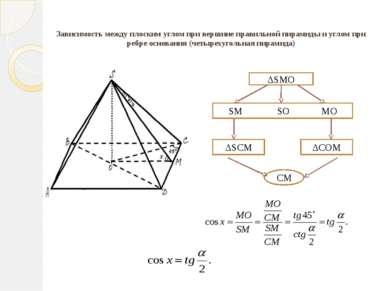Зависимость между плоским углом при вершине правильной пирамиды и углом при ребре основания (четырехугольная пирамида) ΔSMO SM SO MO ΔSCM ΔCOM CM
Cлайд 11
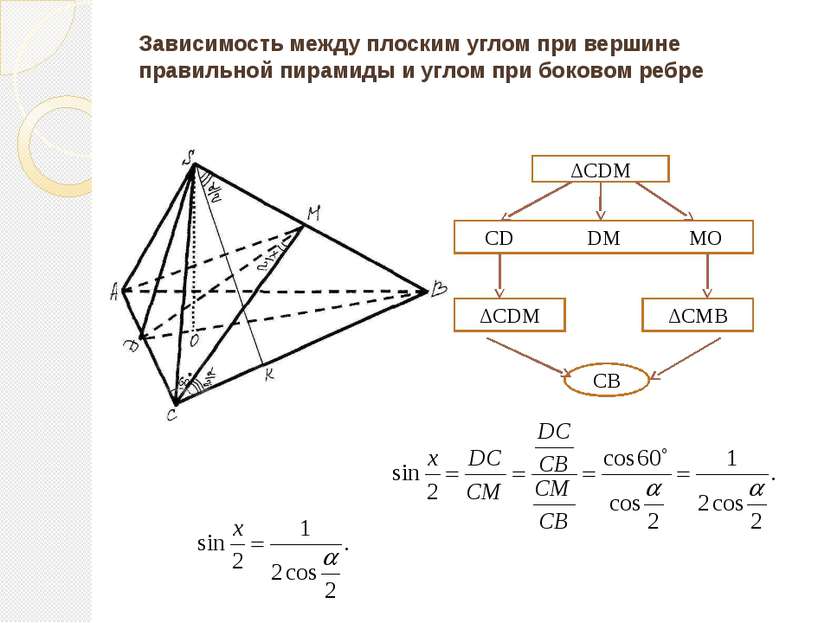
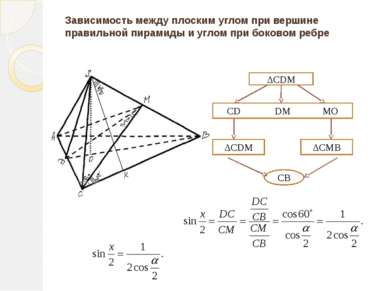Зависимость между плоским углом при вершине правильной пирамиды и углом при боковом ребре ΔCDM CD DM MO ΔCDM ΔCMB CB
Cлайд 12
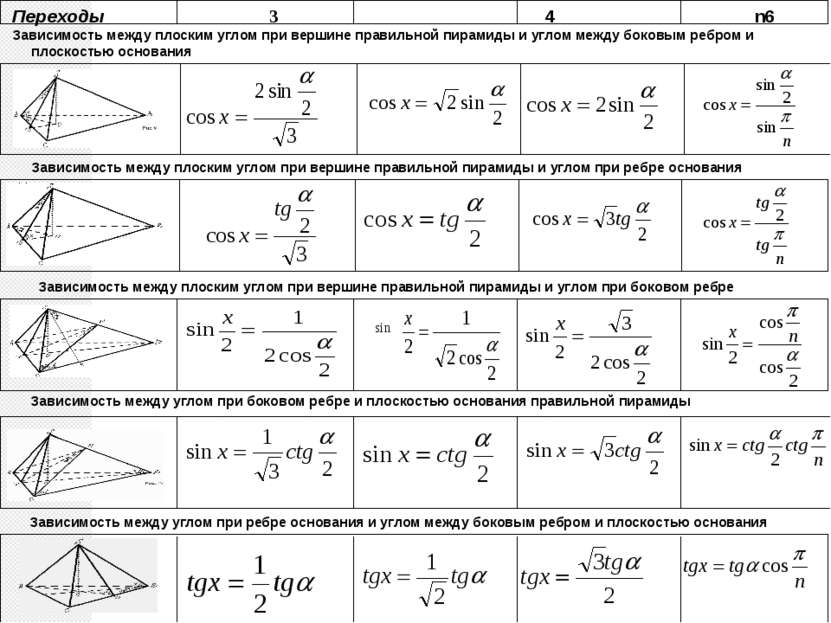
РАБОТА В ГРУППАХ Переходы N=3 N=4 Зависимость между плоским углом при вершине правильной пирамиды и углом между боковым ребром и плоскостью основания Зависимость между плоским углом при вершине правильной пирамиды и углом при ребре основания Зависимость между плоским углом при вершине правильной пирамиды и углом при боковом ребре
Cлайд 13
РАБОТА В ГРУППАХ Переходы N=3 N=4 Зависимость между плоским углом при вершине правильной пирамиды и углом между боковым ребром и плоскостью основания Зависимость между плоским углом при вершине правильной пирамиды и углом при ребре основания Зависимость между плоским углом при вершине правильной пирамиды и углом при боковом ребре
Cлайд 14
Вернемся к задаче 255 1. Из ΔАВС найдем . 2. Применим формулу перехода для ∟DMO=X: , отсюда . 3. По теореме Пифагора DO= = 4 = = . Ответ: В правильной треугольной пирамиде сторона основания равна 8 см, а плоский угол при вершине равен φ найдите высоту пирамиды.
Cлайд 15
Переходы 3 4 6 Зависимость между плоским углом при вершине правильной пирамиды и углом между боковым ребром и плоскостью основания Зависимость между плоским углом при вершине правильной пирамиды и углом при ребре основания Зависимость между плоским углом при вершине правильной пирамиды и углом при боковом ребре n Зависимость между углом при боковом ребре и плоскостью основания правильной пирамиды Зависимость между углом при ребре основания и углом между боковым ребром и плоскостью основания
Cлайд 16
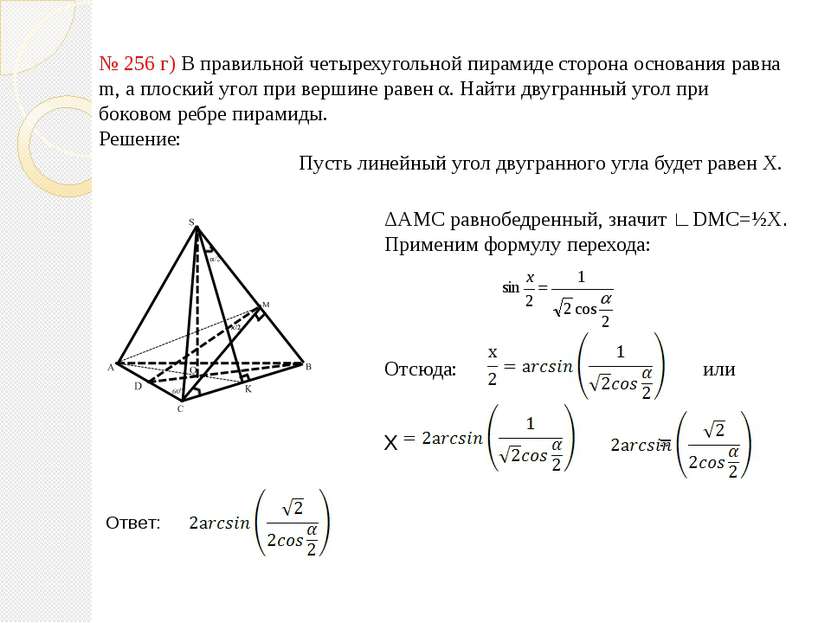
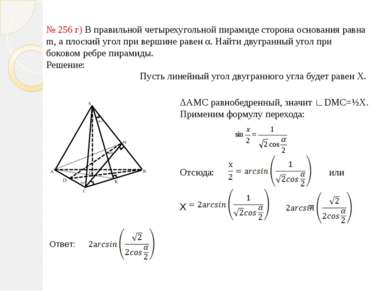№ 256 г) В правильной четырехугольной пирамиде сторона основания равна m, а плоский угол при вершине равен α. Найти двугранный угол при боковом ребре пирамиды. Решение: Пусть линейный угол двугранного угла будет равен X. ΔАМС равнобедренный, значит ∟DMC=½X. Применим формулу перехода: Отсюда: или Х = Ответ:
Cлайд 17
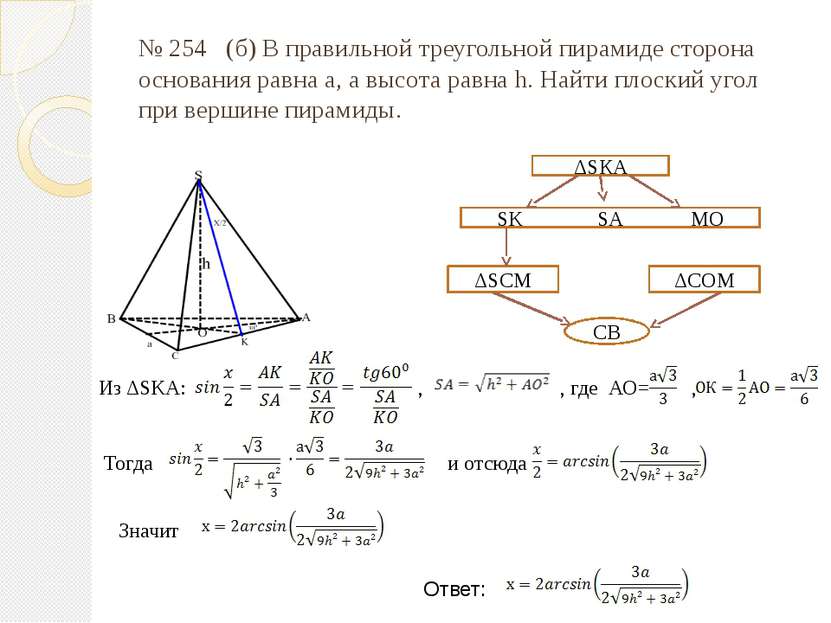
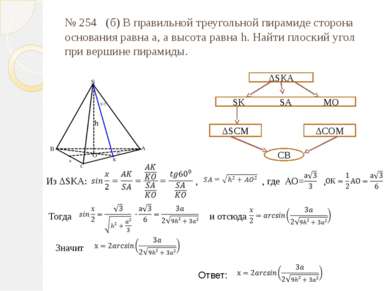№ 254 (б) В правильной треугольной пирамиде сторона основания равна а, а высота равна h. Найти плоский угол при вершине пирамиды. ΔSКА SK SA MO ΔSCM ΔCOM CB Из ΔSKA: , , где АО= , Тогда и отсюда Значит Ответ:
Cлайд 18
Рефлексия Изучили мнемонический прием. Вывели формулы переда основных углов в правильных пирамидах. Научились применять мнемонический прием для доказательства зависимостей между углами в правильной пирамиде и решения задач.
Cлайд 19
Домашнее задание Задача № 254 (б,г,д) – решить двумя способами – традиционно и с помощью мнемонического приема или формул перехода; Изучить теоретический материал урока (см. опорные схемы урока) и мнемонический прием, а так же ознакомиться с презентацией к уроку (см. электронную папку учителя); Дополнительная информация по теме урока содержится в презентации «Это интересно» (см. электронную папку учителя). СПАСИБО ЗА ВНИМАНИЕ
