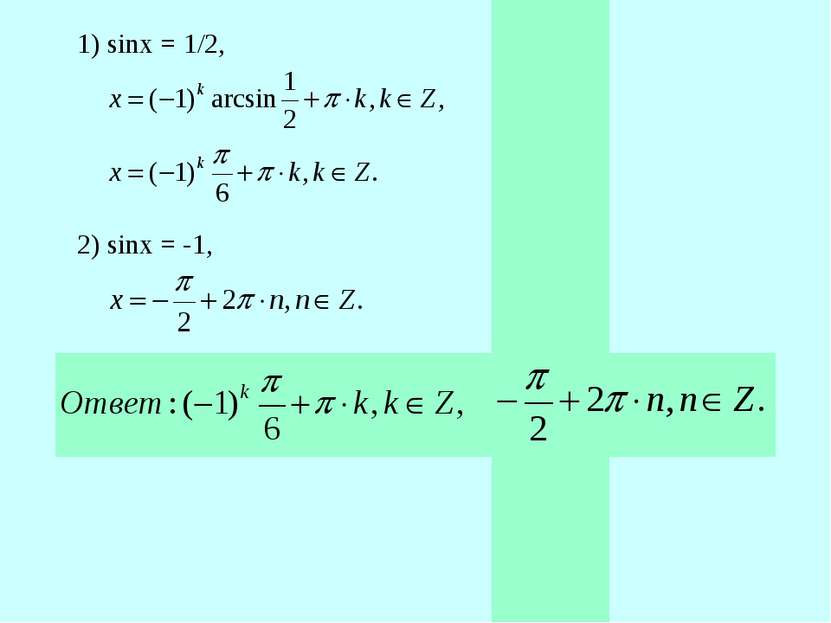X
Код презентации скопируйте его
Тригонометрические уравнения
Скачать эту презентацию
Презентация на тему Тригонометрические уравнения
Скачать эту презентациюCлайд 1
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Cлайд 2
Верно ли, что:
Cлайд 3
Имеют ли смысл выражения:
Cлайд 4
Решить уравнение:
Cлайд 5
Пример 1. Решить уравнение 2 sin2x + sinx - 1 = 0. Решение. Введём новую переменную t = sinx. Тогда данное уравнение примет вид 2t2 + t - 1 = 0. Решим его: D = 1 + 8 = 9, Cледовательно, sinx = 1/2 или sinx = -1.
Cлайд 6
1) sinx = 1/2, 2) sinx = -1,
Cлайд 7
Решение. Заменяя sin2x на 1-сos2x, получим квадратное уравнение относительно сosx. 6 ( 1-cos2x ) + 5 cosx - 2 = 0, -6 cos2x + 5cosx + 4 = 0, 6 cos2x - 5cosx - 4 = 0. Пусть cos x = t, тогда 6t2 - 5t - 4 = 0, t1= - 1/2, t2 = 4/3.
Cлайд 8
Cледовательно, сos x = - 1/2 или cos x = 4/3. Уравнение cos x = 4/3 не имеет решений, так как 4/3 > 1. Решая уравнение сos x = -1/2, находим:
Cлайд 9
Пример 3. Решить уравнение tgx + 2ctgx = 3. то уравнение можно записать в виде: Обозначим tgx через t. Получим уравнение которое приводится к квадратному t2 - 3t + 2 = 0,
Cлайд 10
t2 - 3t + 2 = 0. По теореме, обратной теореме Виета, t1 = 2, t2=1.
Cлайд 11
Пример 4. sin2 4x = 1/4 cos 2x =1/2 Решение. Х= ±π/6 + πn; n Є Ζ
Cлайд 12
Пример 5. 3 sin x +4 cos x =0; Решение. Поделим обе части уравнения на cos x ≠ 0. 3 tg x + 4 =0 ; tg x = -4/3 ;
