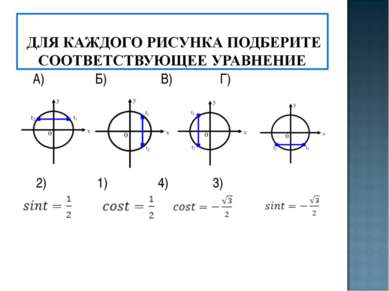
X
Код презентации скопируйте его
Тригонометрические уравнения (10 класс)
Скачать эту презентацию
Презентация на тему Тригонометрические уравнения (10 класс)
Скачать эту презентациюCлайд 1
Учитель 1 квалификационной категории Алейникова Л.В. МБОУ «Гатчинская средняя общеобразовательная школа №1»
Cлайд 2
2 3 4 5 1
Cлайд 3
2 3 4 5 т р и г о н о м е т р и я
Cлайд 4
а 3 4 5 т р и г о н о м е т р и я к с и н у с
Cлайд 5
а к 4 5 т р и г о н о м е т р и я к т с а и н н г у е с н с
Cлайд 6
а к к 5 т р и г о н о м е т р и я к т с с а и и н н н г у у е с с н с
Cлайд 7
а к к о т р и г о н о м е т р и я к т с д с а и и и н н н н г у а у е с т с н а с
Cлайд 8
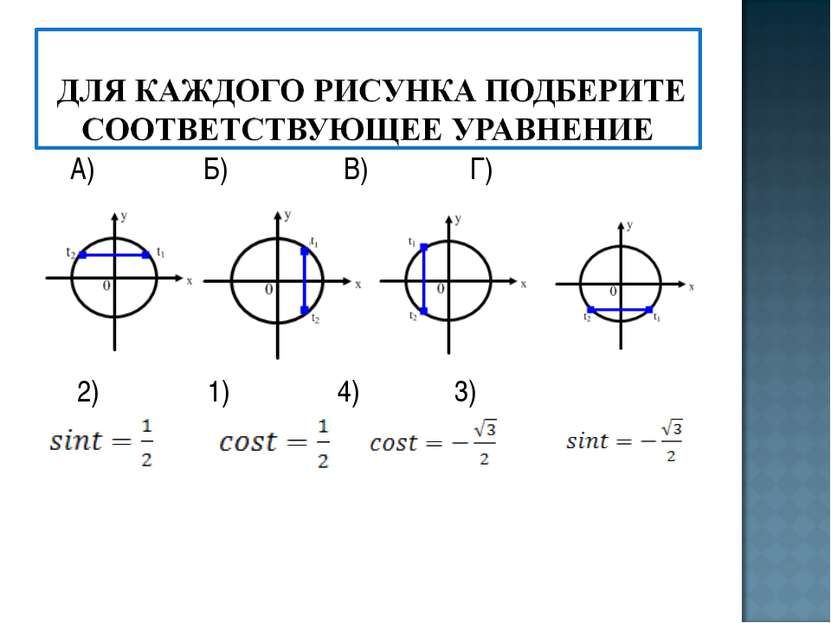
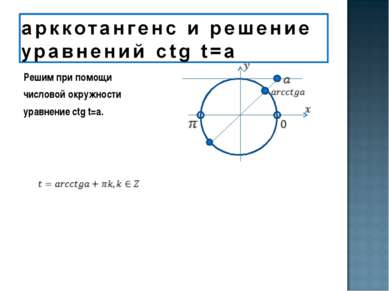
1) уметь отмечать точки на числовой окружности; 2) уметь определять значения синуса, косинуса, тангенса и котангенса для координат точек числовой окружности; 3) знать свойства основных тригонометрических функций; 4) знать понятие арксинуса, арккосинуса, арктангенса, арккотангенса и уметь отмечать их на числовой окружности.
Cлайд 9
Cлайд 10
Cлайд 11
А) Б) В) Г) 1) 2) 3) 4)
Cлайд 12
А) Б) В) Г) 2) 1) 4) 3)
Cлайд 13
1) sin x = 0 а) 2) cos x = -1 б) 3) sin x = 1 в) 4) tg x = 1 г) 5) ctgx = 0 д)
Cлайд 14
1) sin x = 0 а) 2) cos x = -1 б) 3) sin x = 1 в) 4) tg x = 1 г) 5) ctgx = 0 д)
Cлайд 15
1) sin x = 0 а) 2) cos x = -1 б) 3) sin x = 1 в) 4) tg x = 1 г) 5) ctgx = 0 д)
Cлайд 16
1) sin x = 0 а) 2) cos x = -1 б) 3) sin x = 1 в) 4) tg x = 1 г) 5) ctgx = 0 д)
Cлайд 17
1) sin x = 0 а) 2) cos x = -1 б) 3) sin x = 1 в) 4) tg x = 1 г) 5) ctgx = 0 д)
Cлайд 18
1) sin x = 0 а) 2) cos x = -1 б) 3) sin x = 1 в) 4) tg x = 1 г) 5) ctgx = 0 д)
Cлайд 19
Решим при помощи числовой окружности уравнение sin t=a, IаI
Cлайд 20
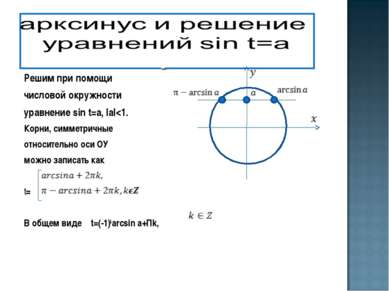
Частные случаи: а = 0 а = -1 а = 1 t = π k, t = π/2+ 2 π k, t = π/2 + 2πk, kєZ k є Z kє Z аrcsin (-а) = - аrcsin а t π /6 π /4 π /3 sint 1/2 √2 / 2 √3 / 2
Cлайд 21
Решим при помощи числовой окружности уравнение cos t=a, IаI
Cлайд 22
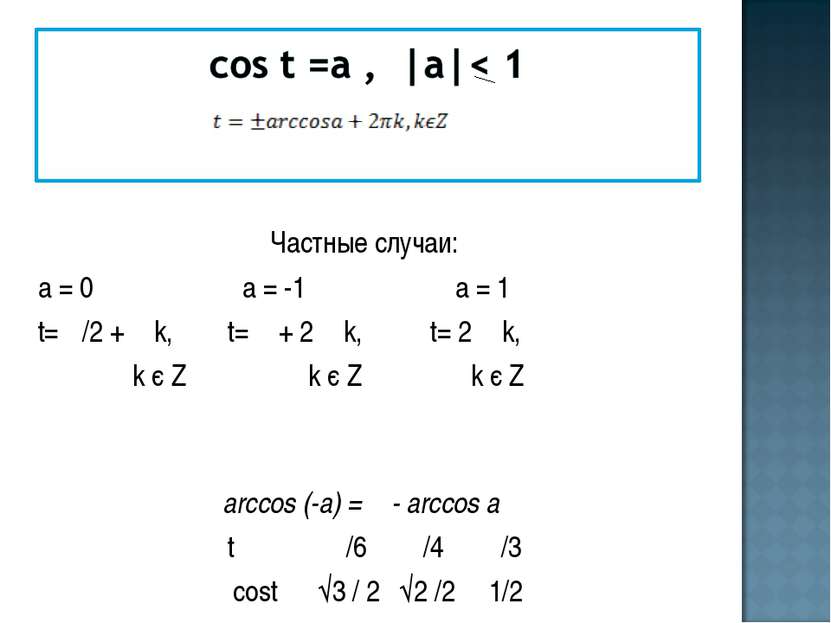
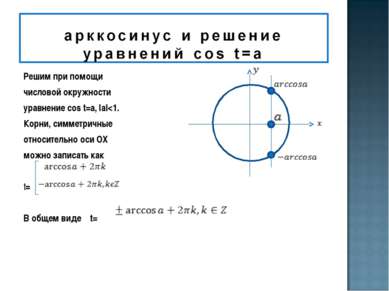
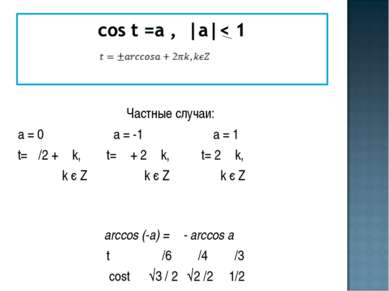Частные случаи: а = 0 а = -1 а = 1 t= π/2 + π k, t= π + 2 π k, t= 2 π k, k є Z k є Z k є Z аrcсos (-а) = π - аrcсos а t π /6 π /4 π /3 cost √3 / 2 √2 /2 1/2
Cлайд 23
Решим при помощи числовой окружности уравнение tg t=a.
Cлайд 24
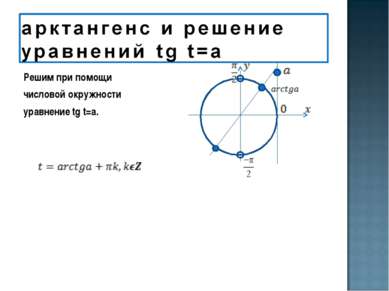
Частные случаи: а = 0 а = -1 а = 1 t = πk, k є Z t = -π/4 + π k t = π/4 + π k аrctg (-а) = - аrctg а t π /6 π /4 π /3 tg t √3 / 3 1 √3
Cлайд 25
Решим при помощи числовой окружности уравнение ctg t=a.
Cлайд 26
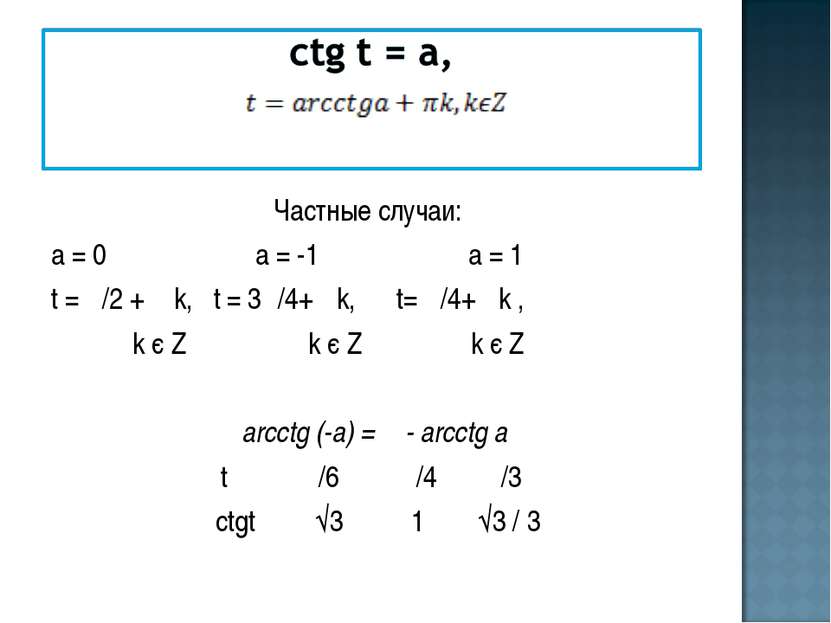
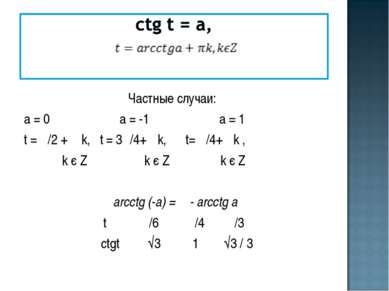Частные случаи: а = 0 а = -1 а = 1 t = π/2 + π k, t = 3π/4+ πk, t= π/4+ πk , k є Z k є Z k є Z аrcсtg (-а) = π - аrcсtg а t π /6 π /4 π /3 ctgt √3 1 √3 / 3
Cлайд 27
а=0 а=1 а=-1 |a|< 1
Cлайд 28
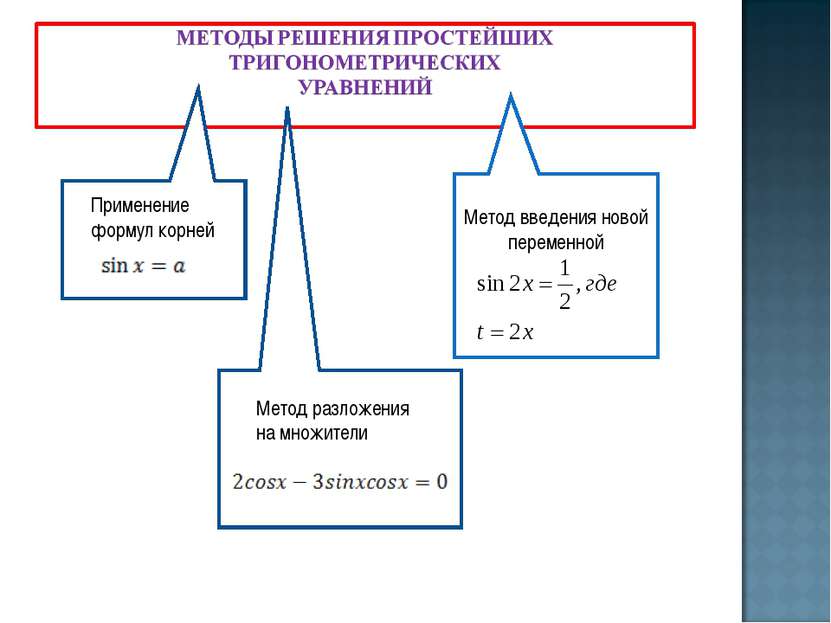
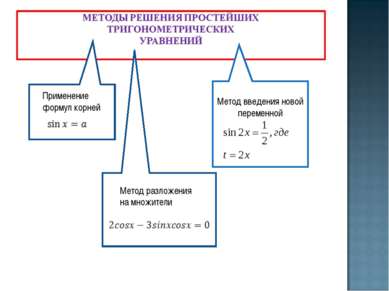ghb Применение формул корней Метод введения новой переменной V Метод разложения на множители
Cлайд 29
Cлайд 30
х= ±arccos а + 2 k, k є Z
Cлайд 31
х = (-1)n arcsin a+πn,n є z 2х = (-1)n 2х = (-1)n х = (-1)n Ответ: (-1)n
Cлайд 32
Это частный вид уравнения cos t=0, t=
Cлайд 33
x = arctg a + πk,k є z
Cлайд 34
Уровень А Уровень Б Решите уравнения: 1. 1. 2. 2. 3. 3. n/n ответ код n/n ответ код 1 Решений нет С 5 М 2 К 6 Р 3 А 7 П 4 у 8 О
Cлайд 35
Уровень А Уровень Б УРА САМ
Cлайд 36
Имеется функция , где I – сила переменного тока . Определить такие моменты времени t, когда сила тока I равна 2 амперам.
