X
Код презентации скопируйте его
Умножение натуральных чисел и его свойства
Скачать эту презентацию
Презентация на тему Умножение натуральных чисел и его свойства
Скачать эту презентациюCлайд 1
Умножение натуральных чисел и его свойства урок математики, 5 класс, УМК Н.Я. Виленкин Автор: Лазарчук Владимир Николаевич, учитель математики и физики МБОУ СОШ № 4 н.п. Енский Ковдорского района Мурманской области
Cлайд 2
Цель Повторить компоненты произведения чисел. Изучить понятие произведения натуральных чисел. Изучить переместительное и сочетательное свойства умножения..
Cлайд 3
: 5 25 125 40 200 50 5 55 165 +15 · 5 : 4 : 10 +? · 3 - 40 11 Вычисли
Cлайд 4
Восстанови цепочку вычислений 60 69 23 8 96 48 + 9 : 3 - 15 · 12 : 2 + 12
Cлайд 5
Cлайд 6
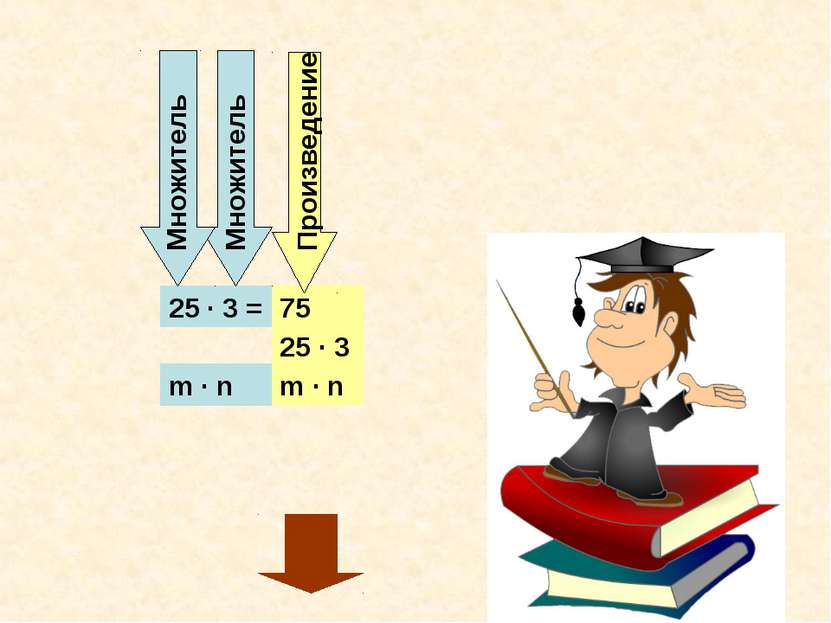
Решим задачу Концертный зал освещается тремя люстрами по 25 лампочек в каждой. Сколько всего лампочек освещают концертный зал? Решение: 25 + 25 + 25 = 75 Сумму, в которой все слагаемые равны друг другу записывают короче: 25 · 3 = 75
Cлайд 7
25 · 3 = 25 · 3 75 m · n m · n Множитель Множитель Произведение
Cлайд 8
Умножить число m на натуральное число n – значит найти сумму n слагаемых, каждое из которых равно m. Выражение m · n и значение этого выражения называют произведением чисел m и n. Числа m и n называют множителями.
Cлайд 9
Представьте в виде произведения 236 + 236 + 236 + 236 = 236 · 4 у + у + у + у + у + у + у = у · 7 (х+5) + (х+5) + (х+5) = (х+5) · 3
Cлайд 10
Как можно вычислить количество фигур? 4 · 6 6 · 4 = 4 · 6 6 · 4 = 30
Cлайд 11
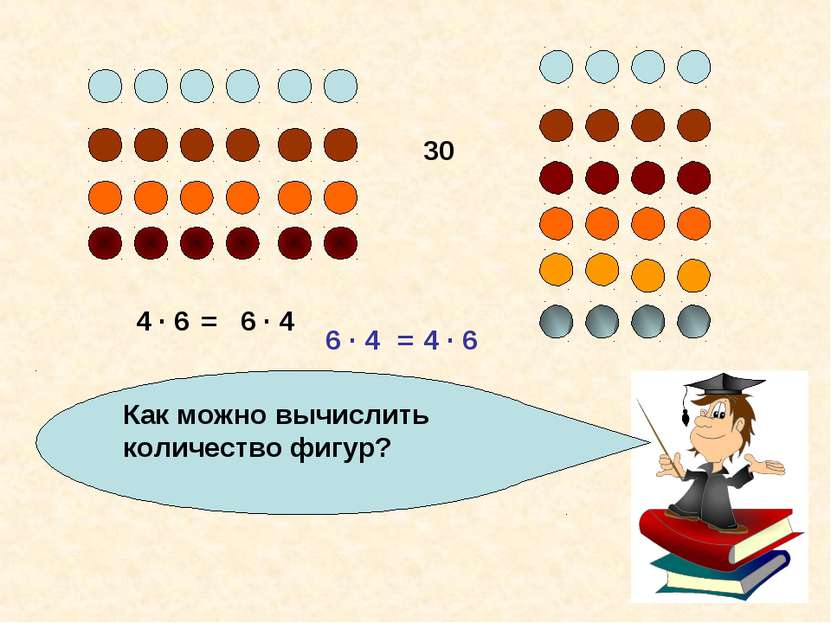
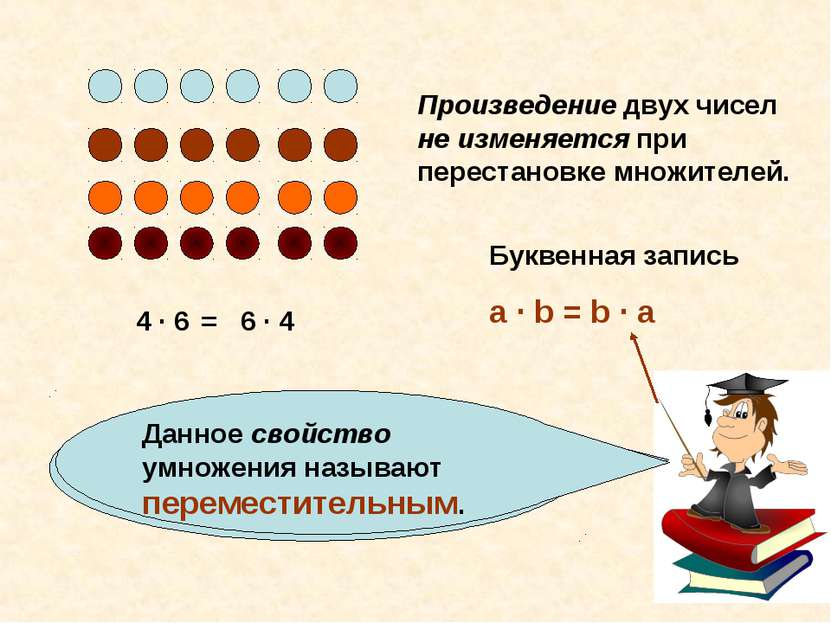
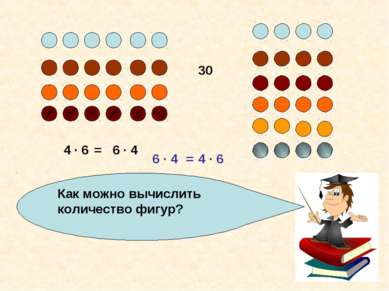
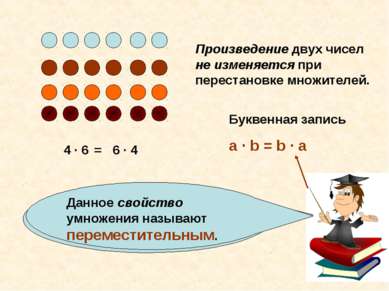Какой можно сделать вывод? 4 · 6 6 · 4 = Произведение двух чисел не изменяется при перестановке множителей. Данное свойство умножения называют переместительным. Буквенная запись a · b = b · a
Cлайд 12
Как можно вычислить количество фигур? (6 · 4) · 2 6 · (4 · 2) = (6 · 4) · 2 6 · (4 · 2) =
Cлайд 13
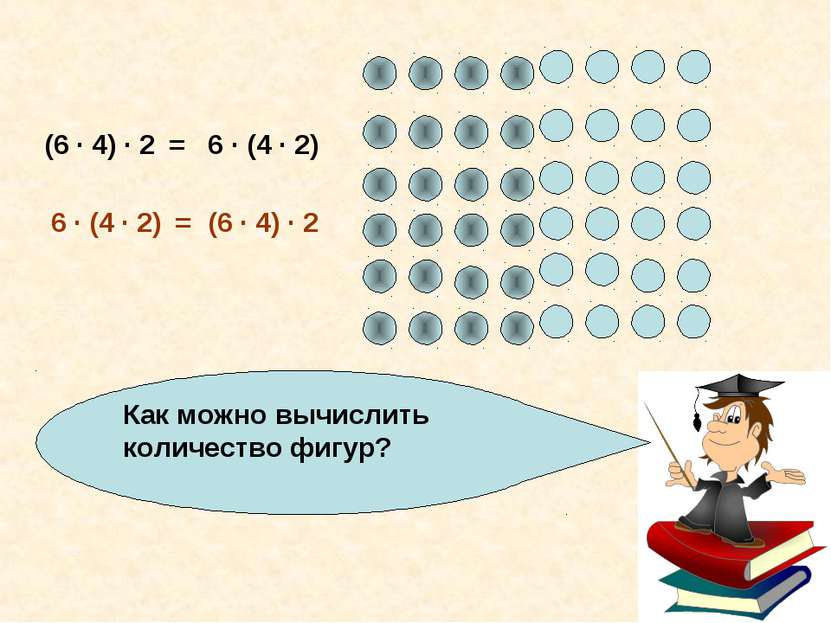
Данное свойство умножения называют сочетательным (6 · 4) · 2 6 · (4 · 2) = (6 · 4) · 2 6 · (4 · 2) = Буквенная запись a · (b · с) = (a · b) · с Чтобы умножить число на произведение двух чисел, можно его умножить сначала на первый множитель, а потом полученное произведение умножить на второй множитель.
Cлайд 14
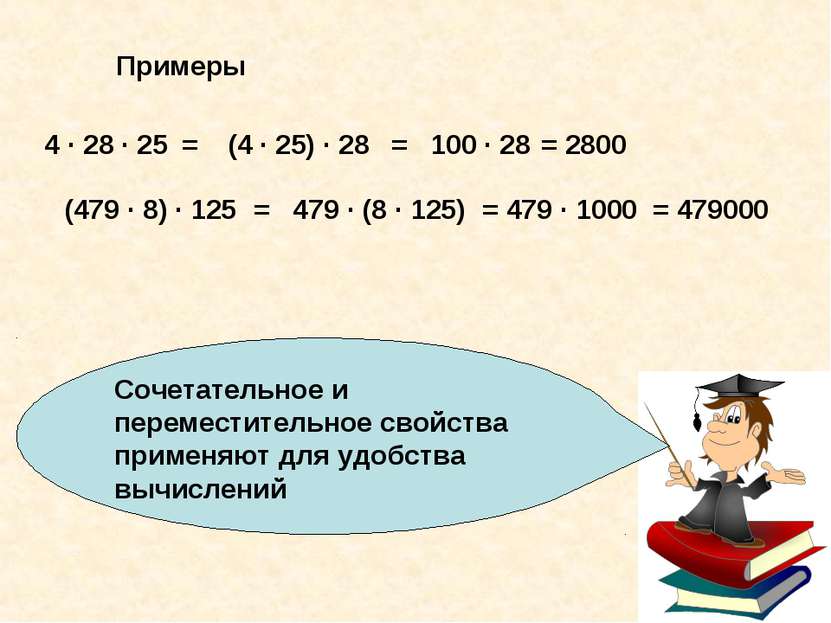
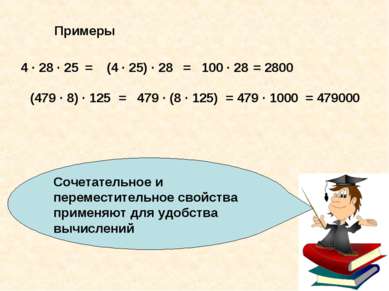Сочетательное и переместительное свойства применяют для удобства вычислений Примеры 4 · 28 · 25 = (4 · 25) · 28 = 100 · 28 = 2800 (479 · 8) · 125 = 479 · (8 · 125) = 479 · 1000 = 479000
Cлайд 15
Напомним еще некоторые свойства умножения, известные из начальной школы Сумма n слагаемых, каждое из которых равно 1, равна n. Сумма n слагаемых, каждое из которых равно 0, равна 0. 1 · n = n 0 · n = 0
Cлайд 16
Запомните! Перед буквенными множителями обычно не пишут знак умножения: вместо 5 · х пишут 5х, вместо a · b пишут ab . Опускают знак умножения и перед скобками. Например вместо 3 · (х + у) пишут 3(х + у), а вместо (х + 5) · (х – 9) пишут (х + 5)(х – 9)
Cлайд 17
Решите из учебника № 404, 405, 406, 412 (а – е), 414
Cлайд 18
Задание на дом п. 11, № 450, 451, 452
Cлайд 19
Список используемых источников Математика 5 класс: учеб. для общеобразоват. организаций учреждений/ Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбуд. – 33-е изд., стер. – М. : Мнемозина, 2014. – 280 с. : ил.
