X
Код презентации скопируйте его
Определение машины Тьюринга
Скачать эту презентацию
Презентация на тему Определение машины Тьюринга
Скачать эту презентациюCлайд 1
Определение машины Тьюринга
Cлайд 2
Машина Тьюринга – абстрактный исполнитель, осуществляющий алгоритмический процесс Это математический объект, а не физическая машина Предложена Аланом Тьюрингом в 1936 году
Cлайд 3
1) Внешний алфавит А = {a0, a1, …, an} Элемент a0 называется пустой символ В этом алфавите в виде слова кодируется исходный набор данных и результат работы алгоритма Устройство машины Тьюринга
Cлайд 4
2) Внутренний алфавит Q = {q0, q1, …, qm}, {П, Л, С} В любой момент времени машина М находится в одном из состояний q0, q1, …, qm При этом: q1 - начальное состояние q0 - заключительное состояние Символы {П, Л, С} – символы сдвига (вправо, влево, на месте) Устройство машины Тьюринга
Cлайд 5
3) Внешняя память (лента) Машина имеет ленту, разбитую на ячейки, в каждую из которых может быть записана только одна буква Устройство машины Тьюринга
Cлайд 6
3) Внешняя память (лента) Устройство машины Тьюринга Пустая клетка содержит a0. В каждый момент времени на ленте записано конечное число непустых букв Лента является конечной, но дополняется в любой момент ячейками слева и справа для записи новых непустых символов. Это соответствует принципу абстракции потенциальной осуществимости
Cлайд 7
4) Каретка (управляющая головка) Каретка машины располагается над некоторой ячейкой ленты – воспринимает символ, записанный в ячейке В одном такте работы каретка сдвигается на одну ячейку (вправо, влево) или остается на месте Устройство машины Тьюринга
Cлайд 8
5) Функциональная схема (программа) Программа машины состоит из команд: Устройство машины Тьюринга Для каждой пары (qi, aj) программа машины должна содержать одну команду (детерминированная машина Тьюринга)
Cлайд 9
Замечание 1) В недетерминированной машине может появиться несколько параллельных вычислительных процессов 2) Разные машины Тьюринга отличаются своими программами Для каждого алгоритма создается своя машина Тьюринга, точнее ее программа
Cлайд 10
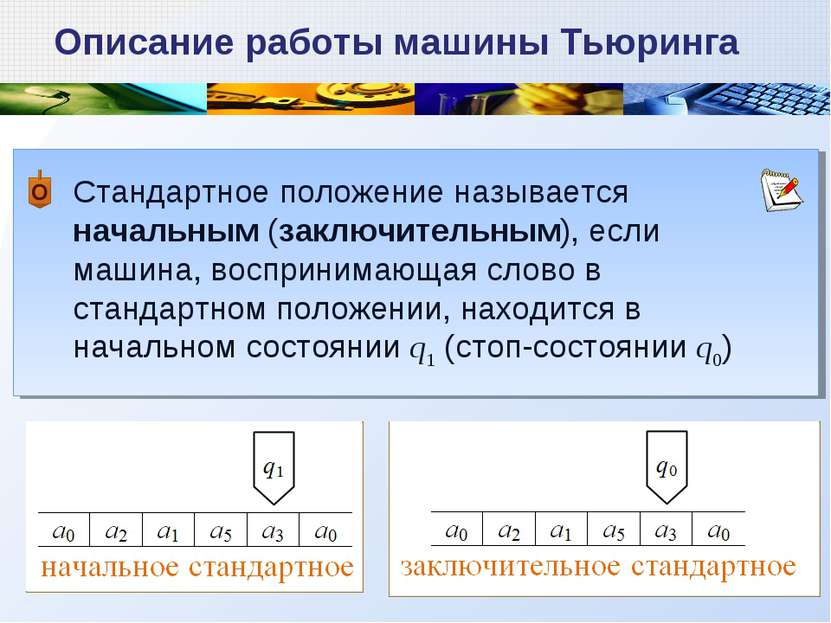
К началу работы машины на ленту подается исходный набор данных в виде слова Описание работы машины Тьюринга Будем говорить, что непустое слово в алфавите А\{a0} воспринимается машиной в стандартном положении, если: - оно задано в последовательных ячейках ленты, - все другие ячейки пусты, - машина обозревает крайнюю правую ячейку из тех, в которых записано слово
Cлайд 11
Описание работы машины Тьюринга Стандартное положение называется начальным (заключительным), если машина, воспринимающая слово в стандартном положении, находится в начальном состоянии q1 (стоп-состоянии q0)
Cлайд 12
Находясь в не заключительном состоянии, машина совершает шаг, который определяется текущим состоянием qi и обозреваемым символом aj Описание работы машины Тьюринга
Cлайд 13
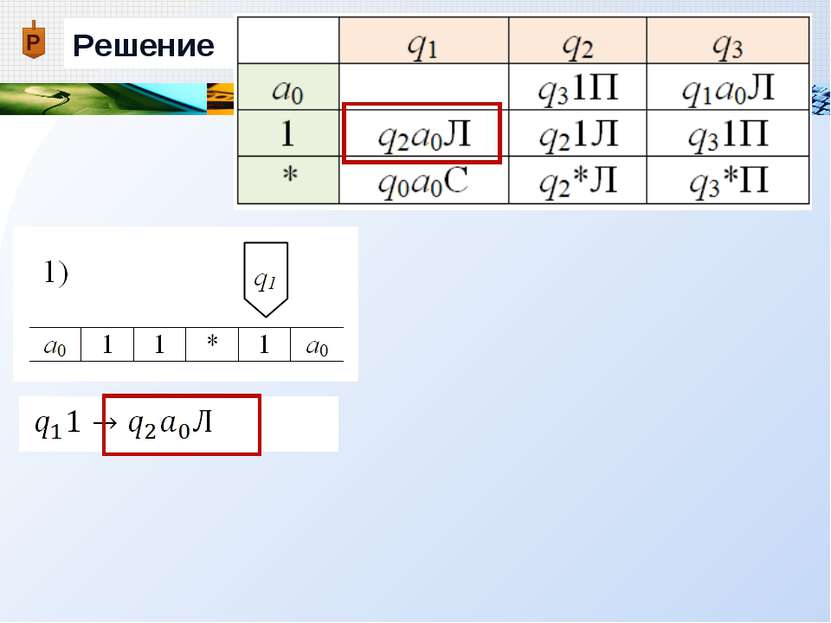
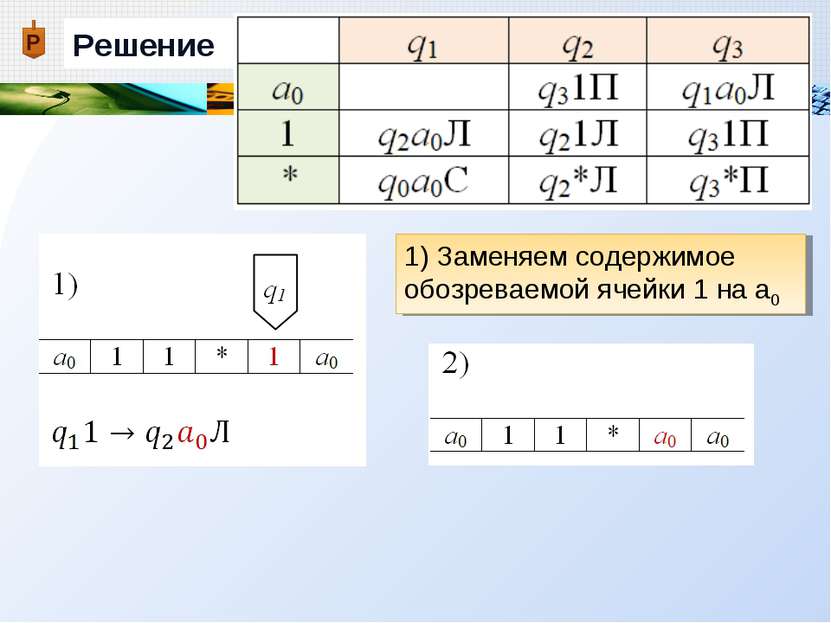
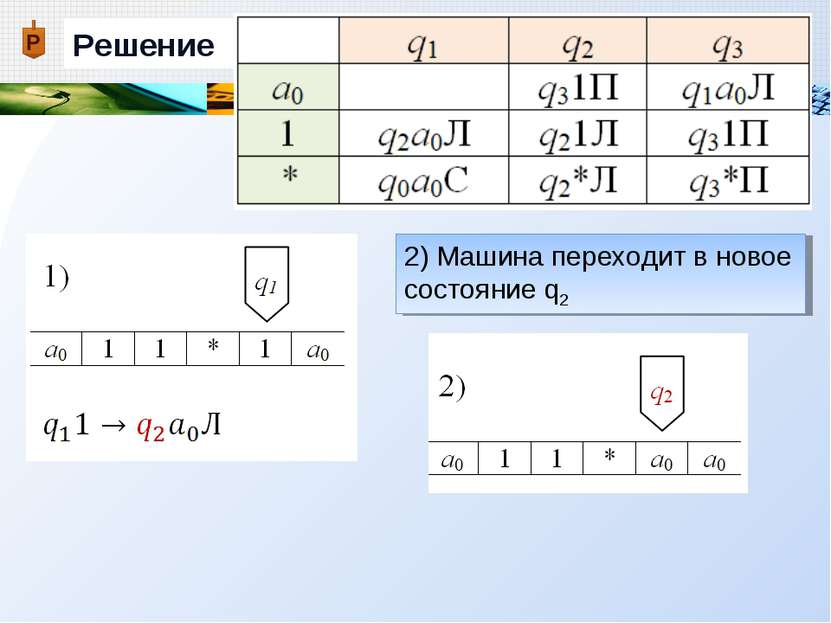
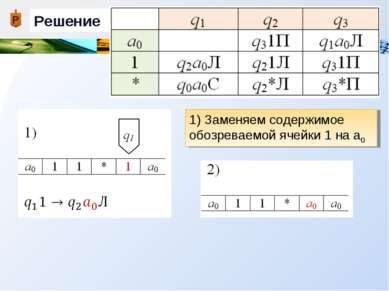
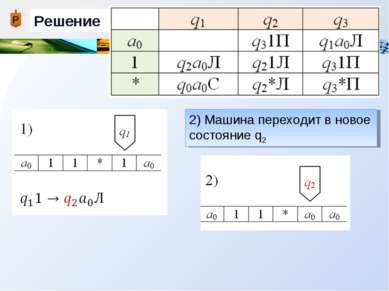
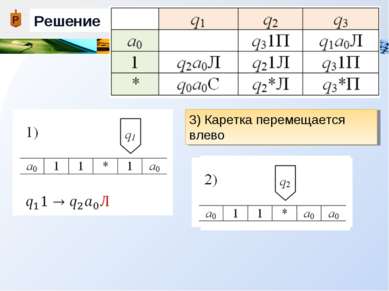
Описание работы машины Тьюринга В соответствии с командой qiaj qkal Х выполняются следующие действия: 1) Содержимое обозреваемой ячейки aj стирается и в нее записывается символ al (который может совпадать с aj) 2) Машина переходит в новое состояние qk (оно может совпадать с состоянием qi) 3) Каретка перемещается в соответствии с управляемым символом Х {П, Л, С}
Cлайд 14
При переходе машины в заключительное состояние q0 ее работа прекращается На ленте записан результат работы алгоритма – слово в алфавите А\{a0} Описание работы машины Тьюринга
Cлайд 15
Машинным словом (конфигурацией) машины Тьюринга называется слово вида 1qkal 2, где 1 и 2 - слова в алфавите А.
Cлайд 16
Конфигурация 1qkal 2 интерпретируется следующим образом: - машина находится в состоянии qk - каретка обозревает на ленте символ al - 1 и 2 – это содержимое ленты до и после символа al
Cлайд 17
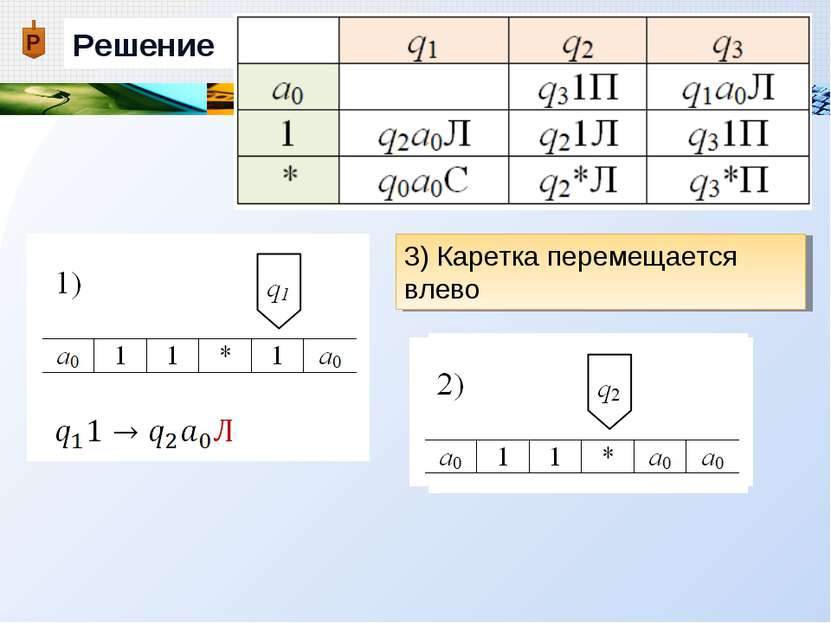
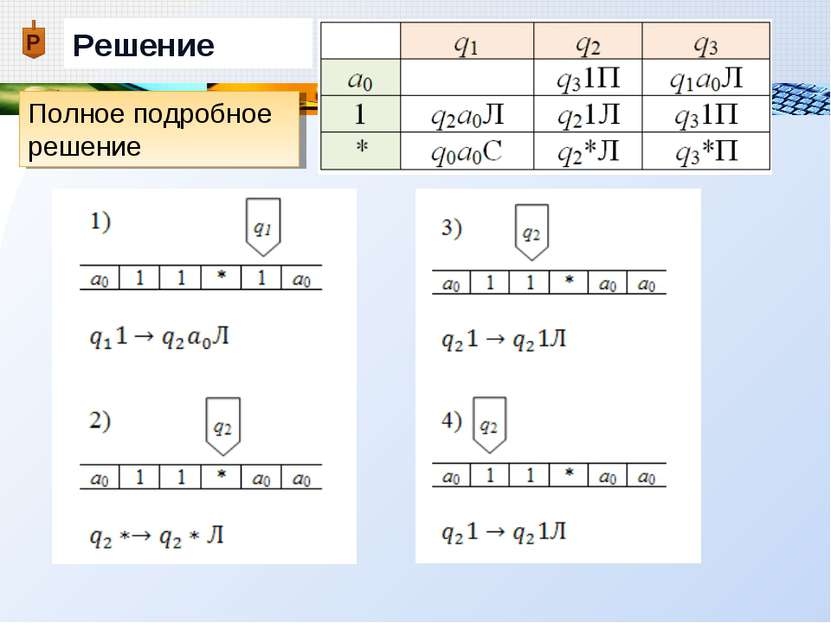
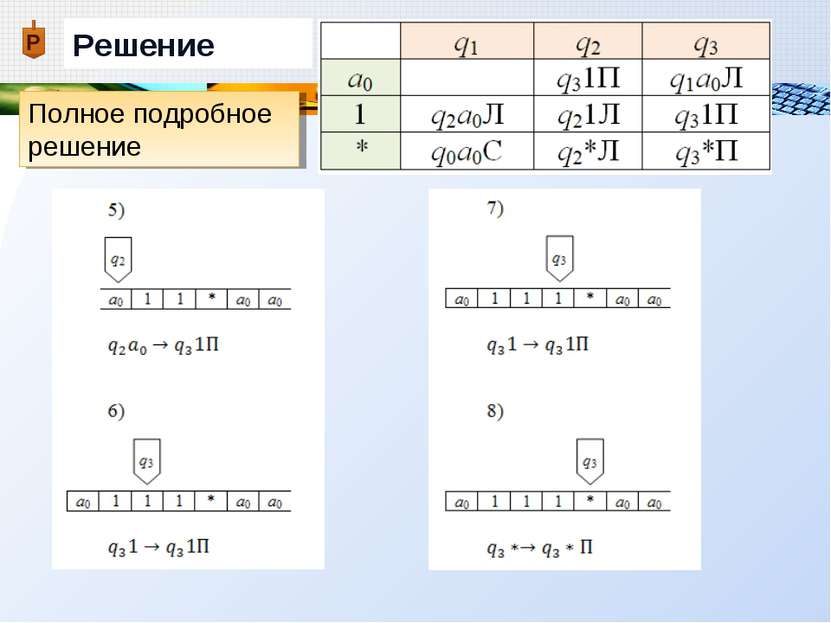
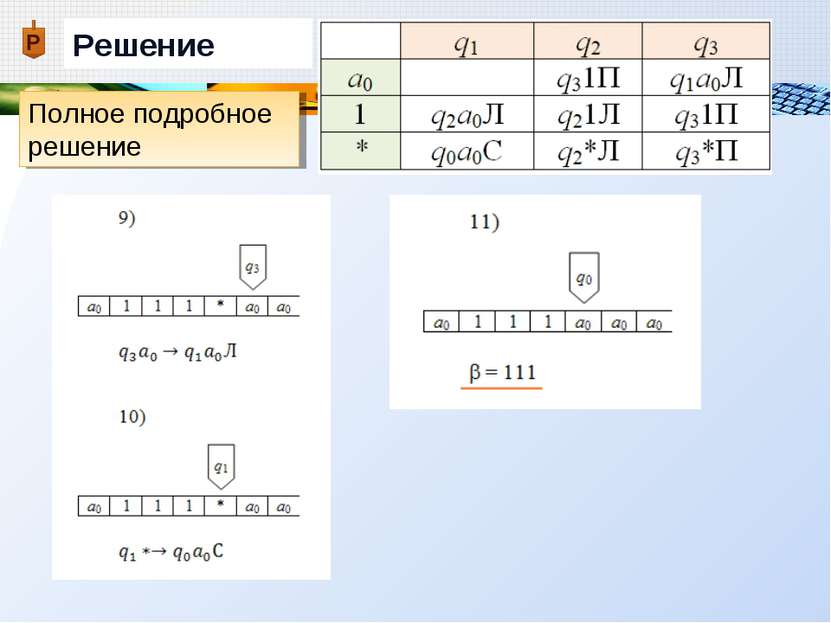
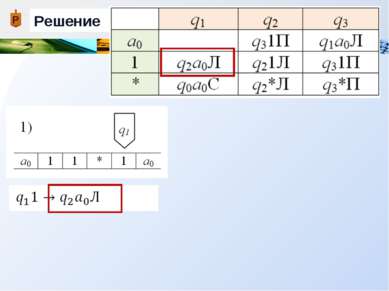
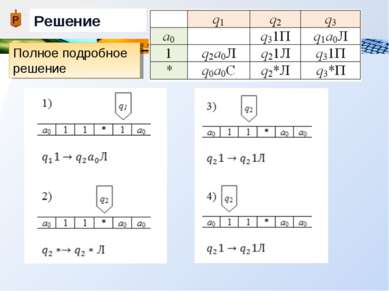
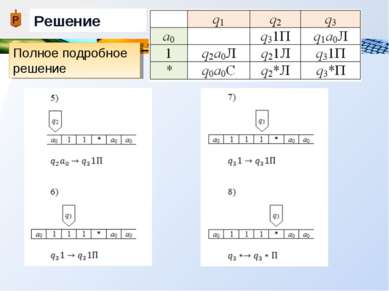
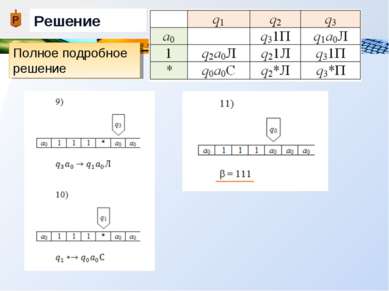
Пример Дана машина Тьюринга с внешним алфавитом А = {a0, 1, * }, алфавитом внутренних состояний Q = {q0, q1, q2, q3}, и следующей функциональной схемой: Применить машину Тьюринга к слову =11*1, начиная со стандартного начального положения
Cлайд 18
Решение
Cлайд 19
Решение 1) Заменяем содержимое обозреваемой ячейки 1 на а0
Cлайд 20
Решение 2) Машина переходит в новое состояние q2
Cлайд 21
Решение 3) Каретка перемещается влево
Cлайд 22
Решение Полное подробное решение
Cлайд 23
Решение Полное подробное решение
Cлайд 24
Решение Полное подробное решение
Cлайд 25
Решение Решение, записанное с помощью конфигураций (в строчку)
Cлайд 26
= 1*11 Ответ: = 111
Cлайд 27
Литература Игошин В.И. Математическая логика и теория алгоритмов. – М.: Академия, 2008. - 448 с. Лихтарников Л.М., Сукачева Т.Г. Математическая логика. Курс лекций. Задачник-практикум и решения. – СПб.: Лань, 1999. - 288 с. Ильиных А.П. Теория алгоритмов. Учебное пособие. – Екатеринбург, 2006. - 149 с.
Cлайд 28
Люди могут вести себя по-разному в одинаковых ситуациях, и этим они принципиально отличаются от машин.
