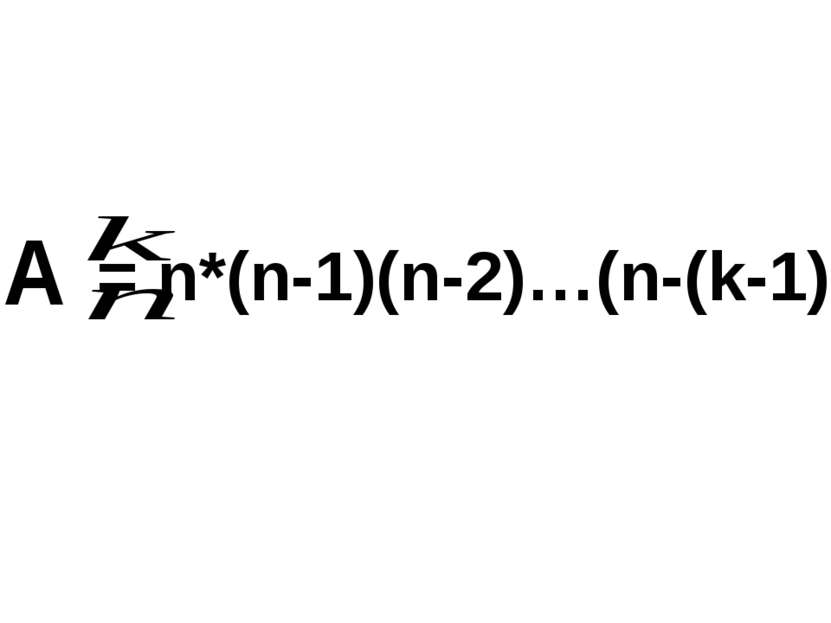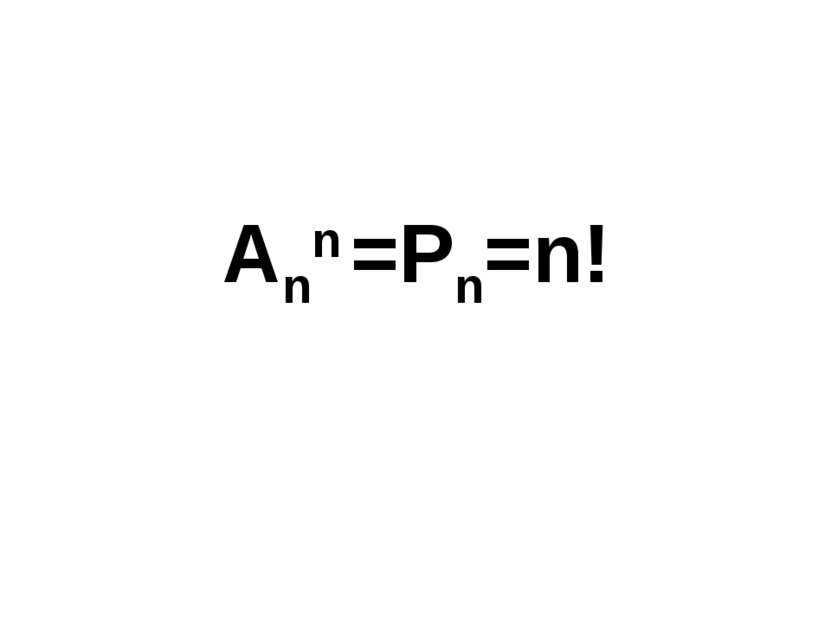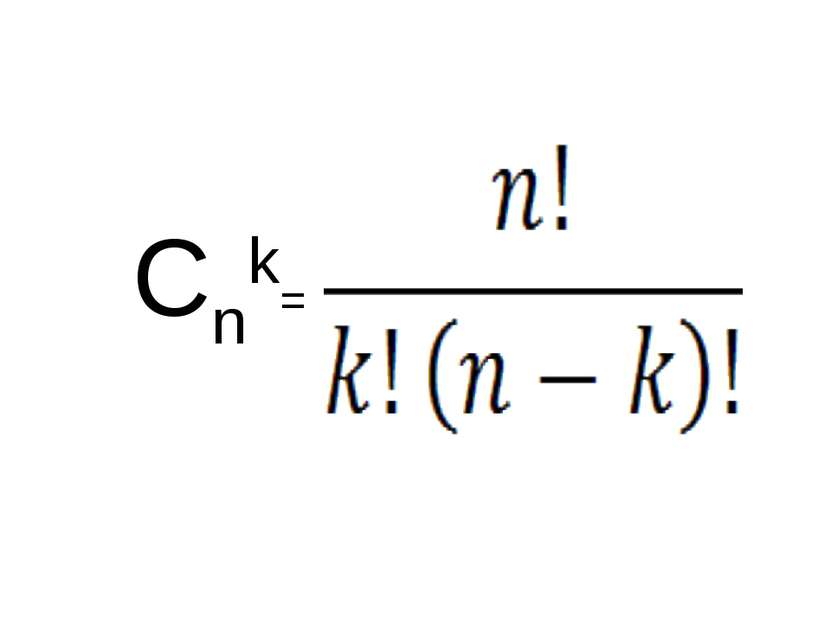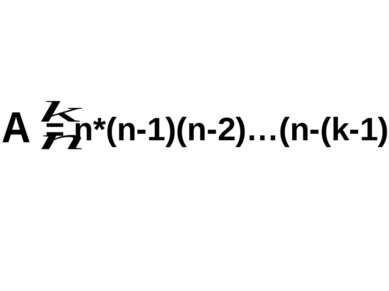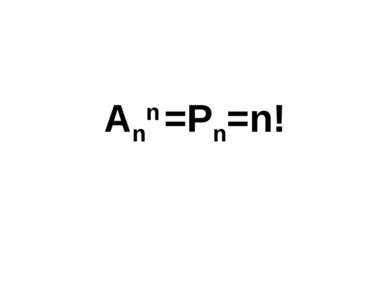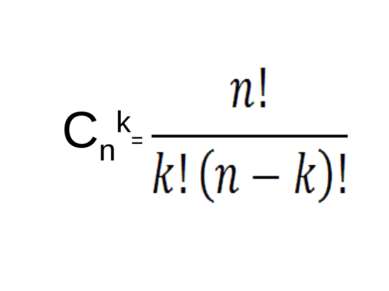X
Код презентации скопируйте его
Комбинаторика. Комбинаторные задачи
Скачать эту презентациюПрезентация на тему Комбинаторика. Комбинаторные задачи
Скачать эту презентациюCлайд 2
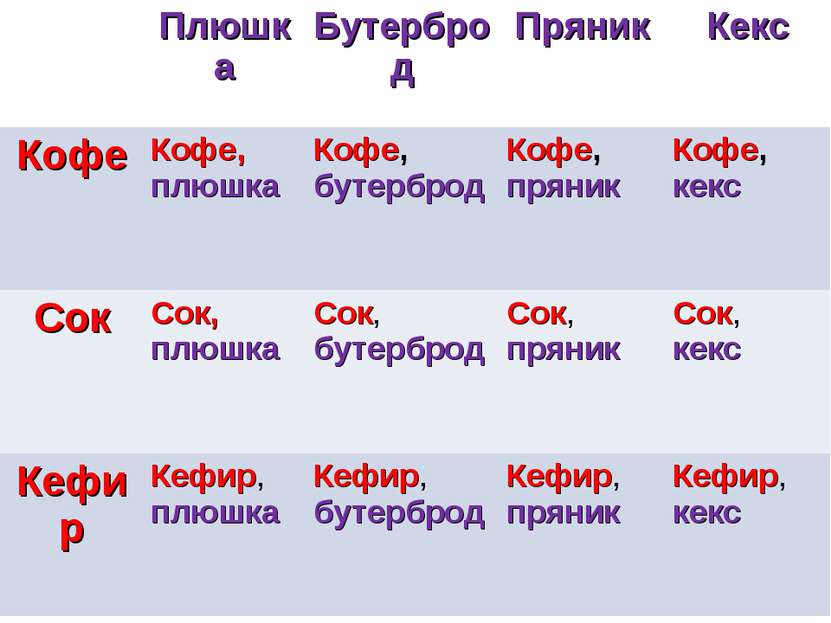
 На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбирать? Пример 1.
На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбирать? Пример 1.
Cлайд 3
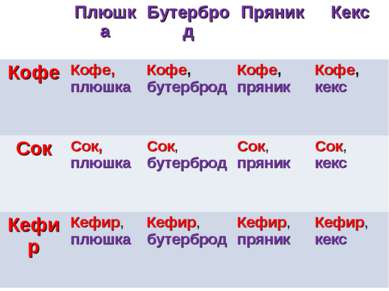 Плюшка Бутерброд Пряник Кекс Кофе Кофе, плюшка Кофе, бутерброд Кофе, пряник Кофе, кекс Сок Сок, плюшка Сок, бутерброд Сок, пряник Сок, кекс Кефир Кефир, плюшка Кефир, бутерброд Кефир, пряник Кефир, кекс
Плюшка Бутерброд Пряник Кекс Кофе Кофе, плюшка Кофе, бутерброд Кофе, пряник Кофе, кекс Сок Сок, плюшка Сок, бутерброд Сок, пряник Сок, кекс Кефир Кефир, плюшка Кефир, бутерброд Кефир, пряник Кефир, кекс
Cлайд 4
 Правило умножения. Для того чтобы найти число всех возможных исходов независимого проведение двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Правило умножения. Для того чтобы найти число всех возможных исходов независимого проведение двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Cлайд 5
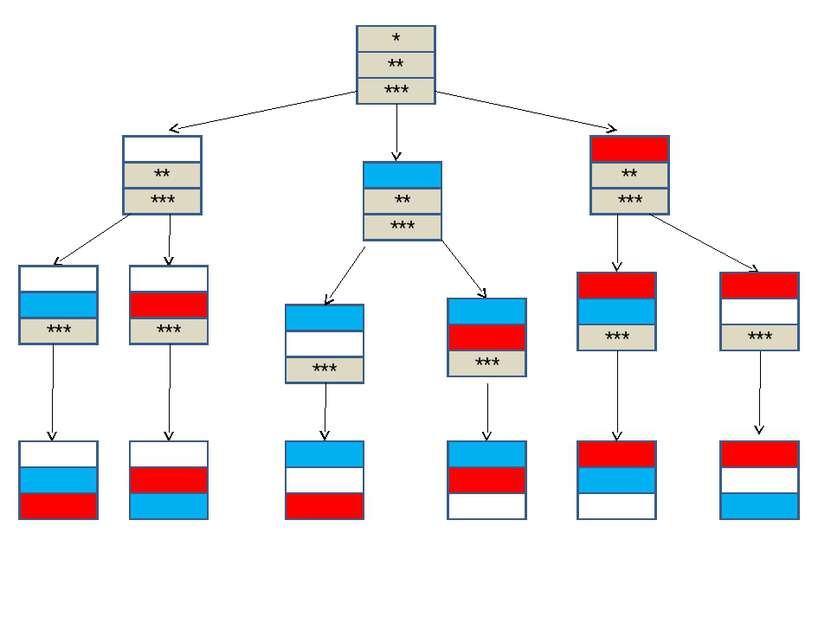
 Пример 2. Несколько стран в качестве символа своего государства решили использовать флаг в виде трех горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг?
Пример 2. Несколько стран в качестве символа своего государства решили использовать флаг в виде трех горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг?
Cлайд 7
 Сколько трехзначных чисел можно составить из цифр 1,3,5 и 7, используя в записи числа каждую из них не более одного раза?
Сколько трехзначных чисел можно составить из цифр 1,3,5 и 7, используя в записи числа каждую из них не более одного раза?
Cлайд 8
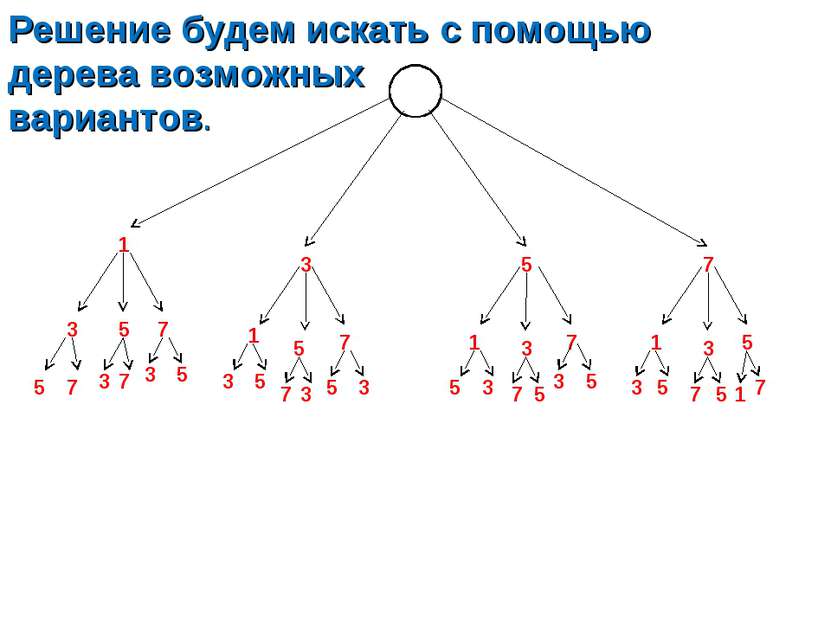
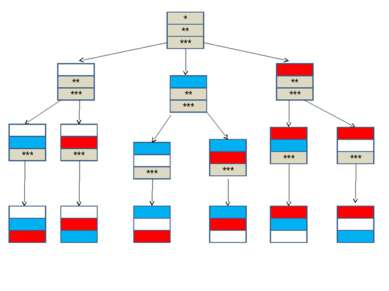
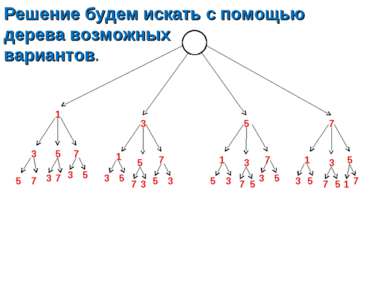 Решение будем искать с помощью дерева возможных вариантов. 1 3 5 7 3 5 7 1 5 7 1 3 7 1 3 5 5 7 3 7 3 5 3 5 7 3 5 3 5 3 7 5 3 5 3 5 7 5 1 7
Решение будем искать с помощью дерева возможных вариантов. 1 3 5 7 3 5 7 1 5 7 1 3 7 1 3 5 5 7 3 7 3 5 3 5 7 3 5 3 5 3 7 5 3 5 3 5 7 5 1 7
Cлайд 9
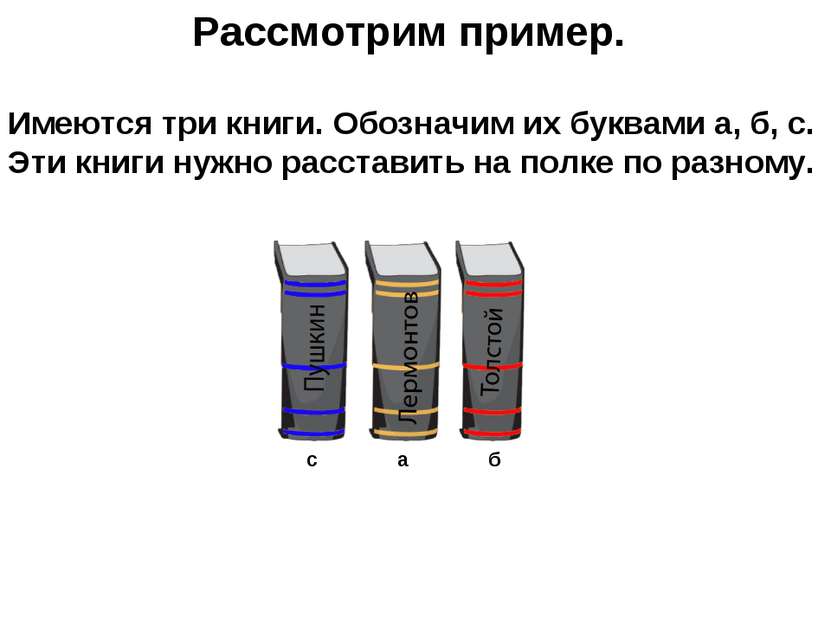
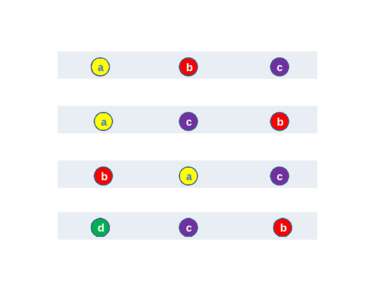
 Рассмотрим пример. Имеются три книги. Обозначим их буквами а, б, с. Эти книги нужно расставить на полке по разному. а б с
Рассмотрим пример. Имеются три книги. Обозначим их буквами а, б, с. Эти книги нужно расставить на полке по разному. а б с
Cлайд 12
 Рассмотрим пример. Имеются три книги. Обозначим их буквами а, б, с. Эти книги нужно расставить на полке по разному. б с а
Рассмотрим пример. Имеются три книги. Обозначим их буквами а, б, с. Эти книги нужно расставить на полке по разному. б с а
Cлайд 13
 Рассмотрим пример. Имеются три книги. Обозначим их буквами а, б, с. Эти книги нужно расставить на полке по разному. с а б
Рассмотрим пример. Имеются три книги. Обозначим их буквами а, б, с. Эти книги нужно расставить на полке по разному. с а б
Cлайд 14
 Рассмотрим пример. Имеются три книги. Обозначим их буквами а, б, с. Эти книги нужно расставить на полке по разному. с б а
Рассмотрим пример. Имеются три книги. Обозначим их буквами а, б, с. Эти книги нужно расставить на полке по разному. с б а
Cлайд 15
 Перестановкой из n элементов называют каждое расположения этих элементов в определенном порядке. Обозначают Pn = n!
Перестановкой из n элементов называют каждое расположения этих элементов в определенном порядке. Обозначают Pn = n!
Cлайд 17
 Задача №2 Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из чисел 0,2,4,6?
Задача №2 Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из чисел 0,2,4,6?
Cлайд 18
 Задача №3 Имеются девять различных книг, четыре из которых учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом?
Задача №3 Имеются девять различных книг, четыре из которых учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом?
Cлайд 19
 Задача № 4 В расписании на понедельник шесть уроков : алгебра, геометрия, биология, история, физкультура, химия. Сколькими способами можно составить расписание уроков на этот день так, чтобы два урока математики стояли рядом. Алгебра Геометрия Биология История Физкультура Химия Алгебра Геометрия История Биология Физкультура Химия Физкультура Геометрия Алгебра История Биология Химия
Задача № 4 В расписании на понедельник шесть уроков : алгебра, геометрия, биология, история, физкультура, химия. Сколькими способами можно составить расписание уроков на этот день так, чтобы два урока математики стояли рядом. Алгебра Геометрия Биология История Физкультура Химия Алгебра Геометрия История Биология Физкультура Химия Физкультура Геометрия Алгебра История Биология Химия
Cлайд 20
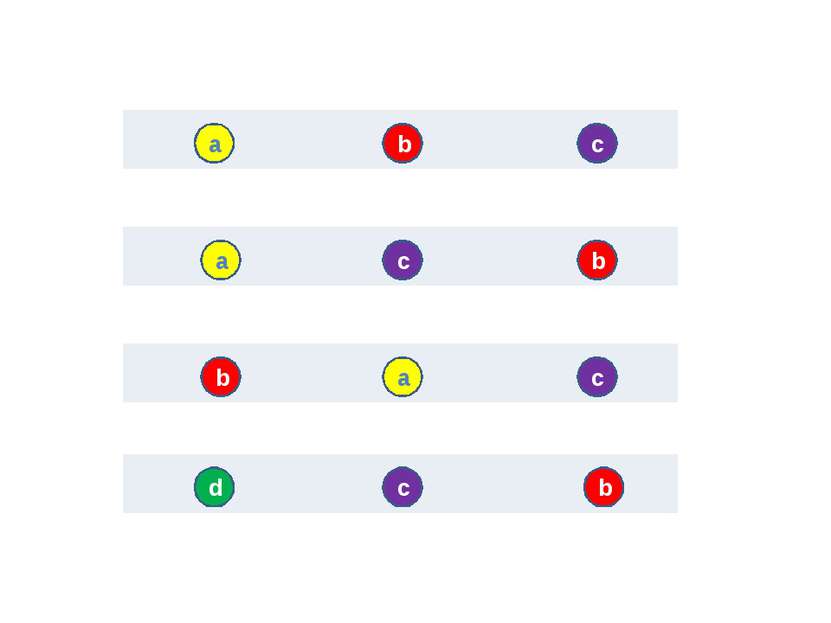
 Пусть имеются 4 шара и 3 пустых ячейки. Обозначили шары буквами a, b, c, d. В пустые ячейки можно по – разному разместить три шара из этого набора.
Пусть имеются 4 шара и 3 пустых ячейки. Обозначили шары буквами a, b, c, d. В пустые ячейки можно по – разному разместить три шара из этого набора.
Cлайд 22
 abc, abd, acb, acd, adb, adc, bac, bad, bca, bcd, bda, bdc cab, cad, cba, cbd, cda, cdb dab, dac, dba, dbc, dca, dcb
abc, abd, acb, acd, adb, adc, bac, bad, bca, bcd, bda, bdc cab, cad, cba, cbd, cda, cdb dab, dac, dba, dbc, dca, dcb
Cлайд 26
 Задача № 5 Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета?
Задача № 5 Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета?
Cлайд 27
 Задача №6 На странице альбома 6 свободных мест для фотографий. Сколько существует способов размещения фотографий в свободные места? a) 4 фотографии; b) 6 фотографий.
Задача №6 На странице альбома 6 свободных мест для фотографий. Сколько существует способов размещения фотографий в свободные места? a) 4 фотографии; b) 6 фотографий.
Cлайд 28
 Задача №7 Сколько трехзначных чисел ( без повторения цифр в записи числа) можно составить из цифр 0, 1, 2, 3, 4, 5, и 6?
Задача №7 Сколько трехзначных чисел ( без повторения цифр в записи числа) можно составить из цифр 0, 1, 2, 3, 4, 5, и 6?
Cлайд 30
 Задача №8 Из трехзначных чисел, записанных с помощью цифр 1, 2, 3, 4,5, 6, 7, 8, 9 (без повторений цифр). Сколько таких в которых: a) не встречаются цифры 6 и 7; b) цифра 8 является последней?
Задача №8 Из трехзначных чисел, записанных с помощью цифр 1, 2, 3, 4,5, 6, 7, 8, 9 (без повторений цифр). Сколько таких в которых: a) не встречаются цифры 6 и 7; b) цифра 8 является последней?
Cлайд 31
 Задача №9 Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отличается от 0?
Задача №9 Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отличается от 0?
Cлайд 44
 Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данных n элементов
Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данных n элементов
Cлайд 46
 Задача № 10 Из 15-ти членов туристической группу надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?
Задача № 10 Из 15-ти членов туристической группу надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?
Cлайд 47
 Задача №11 Из вазы с фруктами, где лежит 9 яблок и 6 груш, нужно выбрать 3 яблока и 2 груши. Сколькими способами это можно сделать?
Задача №11 Из вазы с фруктами, где лежит 9 яблок и 6 груш, нужно выбрать 3 яблока и 2 груши. Сколькими способами это можно сделать?
Cлайд 49
 Задача № I В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в олимпиаде?
Задача № I В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в олимпиаде?
Cлайд 50
 Задача № II В лаборатории, в которой работают заведующий и 10 сотрудников, надо отправить в командировку 5 человек. Сколькими способами это можно сделать если, a)заведующий лаборатории должен ехать b) заведующий должен остаться.
Задача № II В лаборатории, в которой работают заведующий и 10 сотрудников, надо отправить в командировку 5 человек. Сколькими способами это можно сделать если, a)заведующий лаборатории должен ехать b) заведующий должен остаться.