X
Код презентации скопируйте его
Числа, которые мы знаем
Скачать эту презентацию
Презентация на тему Числа, которые мы знаем
Скачать эту презентациюCлайд 1
Числа, которые мы знаем… Выполнил ученик 6 класса Сумин Семен 2013 год ИРКУТСКАЯ ОБЛАСТЬ НИЖНЕИЛИМСКИЙ Р-Н п. Игирма МОУ «Игирменская ООШ»
Cлайд 2
Натуральные числа - Это те числа, которыми мы считаем
Cлайд 3
Это числа, которые делятся на 2 Нечетные- Четные - числа, которые не делятся на 2.
Cлайд 4
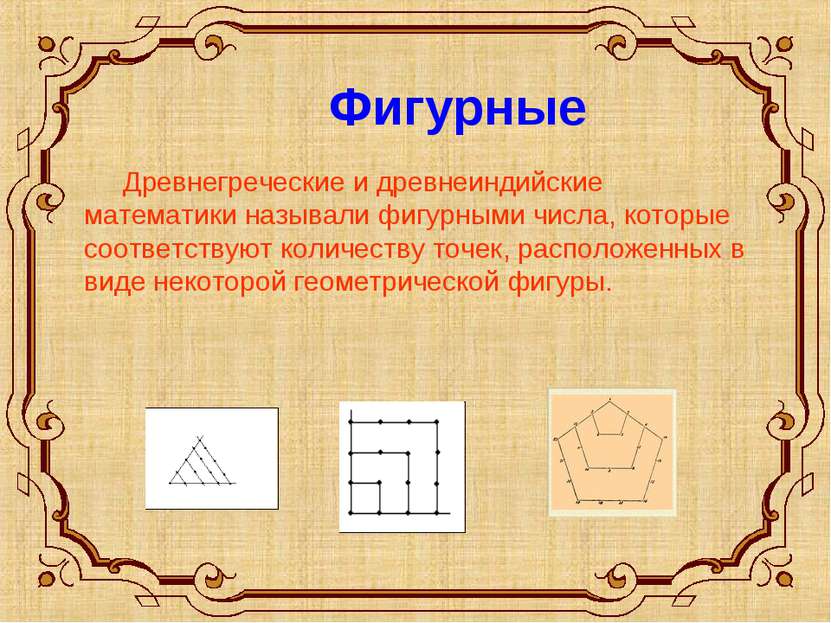
Фигурные Древнегреческие и древнеиндийские математики называли фигурными числа, которые соответствуют количеству точек, расположенных в виде некоторой геометрической фигуры.
Cлайд 5
В древности вычислители часто считали с помощью камешков и, естественно, отмечали случаи, когда камешки можно было сложить в виде правильной фигуры. Фигурные
Cлайд 6
Простые : Число ά, у которого есть только два делителя – 1 и само число ά, называется простым. Например, 7 простое – делится на 1 и 7.
Cлайд 7
Близнецы: Два простых числа, которые отличаются на 2, как 5 и 7, 11 и 13, 17 и 19, получили образное название «близнецы». Любопытно, что в натуральном ряду имеется даже «тройня» - это числа 3, 5, 7. Ну а сколько всего существует близнецов - современной науке неизвестно
Cлайд 8
Совершенные: Совершенными называются числами, равные сумме своих делителей (т. е. всех делителей, включая единицу и исключая само число). Таковы, например, числа 6 и 28, поскольку 6=1+2+3, 28=1+2+4+7+14.
Cлайд 9
Два числа, каждое из которых равно сумме делителей другого числа (не считая самого числа)- называются дружественными Дружественные: Их открыли ученики Пифагора. Пифагорейцы знали только одну пару дружественных чисел: 220 и 284.
Cлайд 10
Составные: Числа, имеющие больше двух делителей называются составными. НАПРИМЕР: 12- составное, делится на 1; 2; 3;4;6;12.
Cлайд 11
ЧИСЛА, НЕ ИМЕЮЩИЕ ОБЩИХ ДЕЛИТЕЛЕЙ (КРОМЕ 1), НАЗЫВАЮТСЯ ВЗАИМНО ПРОСТЫЕ. НАПРИМЕР, 6 (ДЕЛИТЕЛИ 1;2;3;6) И 25 (ДЕЛИТЕЛИ 1;5;25) НОД (6;25)=1
Cлайд 12
Дробные: Термин дробное число (дробь) иногда используется как синоним к термину рациональное число, а иногда синоним любого нецелого числа. В последнем случае, дробные и рациональные числа являются разными вещами, так как тогда нецелые рациональные числа — всего лишь частный случай дробных например: обыкновенные десятичные 0,37; 0, 287;
Cлайд 13
ЦЕЛЫЕ - ЭТО НОЛЬ, ВСЕ НАТУРАЛЬНЫЕ ЧИСЛА И ИМ ПРОТИВОПОЛОЖНЫЕ НАПРИМЕР:
Cлайд 14
Н.Я. ВИЛЕНКИН,В.И. ЖОХОВ, А.С. ЧЕСНОКОВ, С.И. ШВАРЦБУРД. МАТЕМАТИКА Учебник для 6 класса общеобразовательных учреждений. 9 издание, стереотипное мнемозина М. 2001 Н.Б. Истомина Математика 6 класс учебник для 6 класса Смоленск «Ассоциация XXI» 2008 Интернет ресурсы: Википедия ЛИТЕРАТУРА
