X
Код презентации скопируйте его
Алгоритм исследования функции с помощью производной
Скачать эту презентацию
Презентация на тему Алгоритм исследования функции с помощью производной
Скачать эту презентациюCлайд 1
Презентация к уроку Алгоритм исследования функции с помощью производной Преподаватель: Макарова В.В. ГУ «Профессиональный лицей №8» г.Семей 2010г.
Cлайд 2
Cлайд 3
«Дорогу осилит идущий, а математику – мыслящий» Наш сегодняшний урок пройдет под девизом
Cлайд 4
ная Отгадай ребус П ,, ,
Cлайд 5
Кроссворд 1 6 2 4 7 3 5
Cлайд 6
Кроссворд 1 К 6 А 2 4 С А 7 Т 3 Е 5 Л Ь Н А Я
Cлайд 7
Кроссворд 1 К 6 А 2 К 4 С И А Н 7 Т Е 3 Е М 5 Л А Ь Т Н И А К Я А
Cлайд 8
Кроссворд 1 К 6 А 2 К 4 С И А Н 7 Т Е 3 А Е М Р 5 Л А Г Ь Т У Н И М А К Е Я А Н Т
Cлайд 9
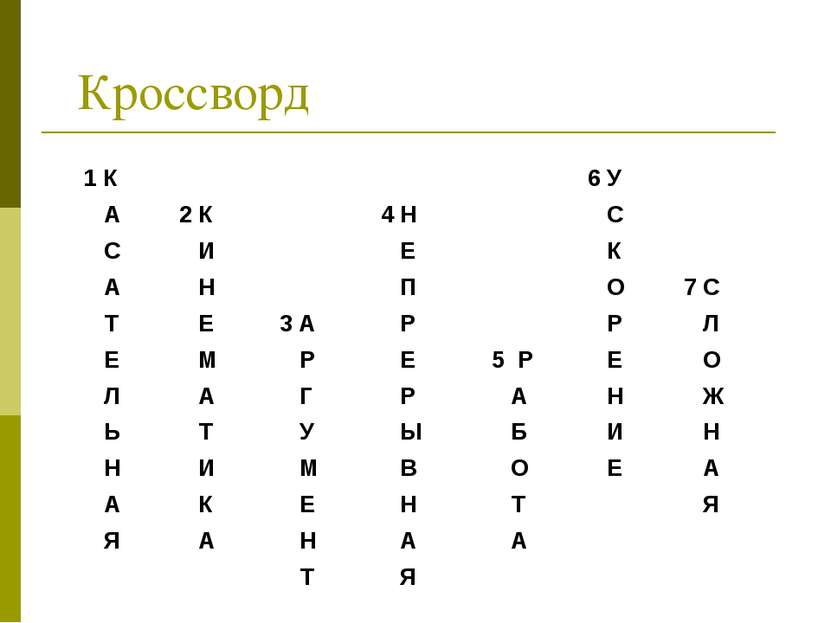
Кроссворд 1 К 6 А 2 К 4 Н С И Е А Н П 7 Т Е 3 А Р Е М Р Е 5 Л А Г Р Ь Т У Ы Н И М В А К Е Н Я А Н А Т Я
Cлайд 10
Кроссворд 1 К 6 А 2 К 4 Н С И Е А Н П 7 Т Е 3 А Р Е М Р Е 5 Р Л А Г Р А Ь Т У Ы Б Н И М В О А К Е Н Т Я А Н А А Т Я
Cлайд 11
Кроссворд 1 К 6 У А 2 К 4 Н С С И Е К А Н П О 7 Т Е 3 А Р Р Е М Р Е 5 Р Е Л А Г Р А Н Ь Т У Ы Б И Н И М В О Е А К Е Н Т Я А Н А А Т Я
Cлайд 12
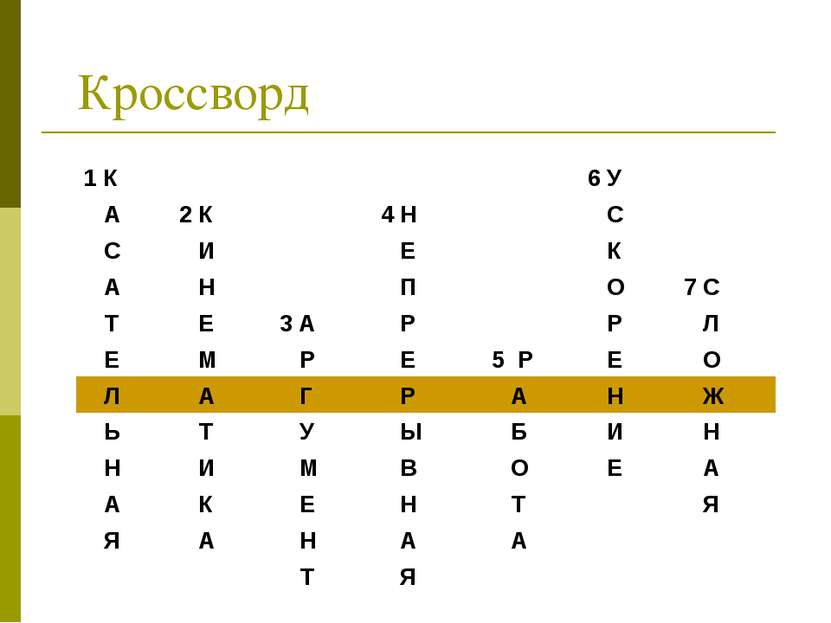
Кроссворд 1 К 6 У А 2 К 4 Н С С И Е К А Н П О 7 С Т Е 3 А Р Р Л Е М Р Е 5 Р Е О Л А Г Р А Н Ж Ь Т У Ы Б И Н Н И М В О Е А А К Е Н Т Я Я А Н А А Т Я
Cлайд 13
Кроссворд 1 К 6 У А 2 К 4 Н С С И Е К А Н П О 7 С Т Е 3 А Р Р Л Е М Р Е 5 Р Е О Л А Г Р А Н Ж Ь Т У Ы Б И Н Н И М В О Е А А К Е Н Т Я Я А Н А А Т Я
Cлайд 14
Лагранж 1736-1813 В 19 лет он стал профессором в Артиллерийской школе Турина. Именно Лагранж в 1791 г. ввёл термин «производная», ему же мы обязаны и современным обозначением производной (с помощью штриха). Термин «вторая производная» и обозначение(два штриха) также ввёл Лангранж (Joseph-Louis Largauge)
Cлайд 15
Основными объектами, изучаемыми в математическом анализе являются функция, ее производная, графики.
Cлайд 16
Как проходит график между двумя точками?
Cлайд 17
Алгоритм исследования функции с помощью производной
Cлайд 18
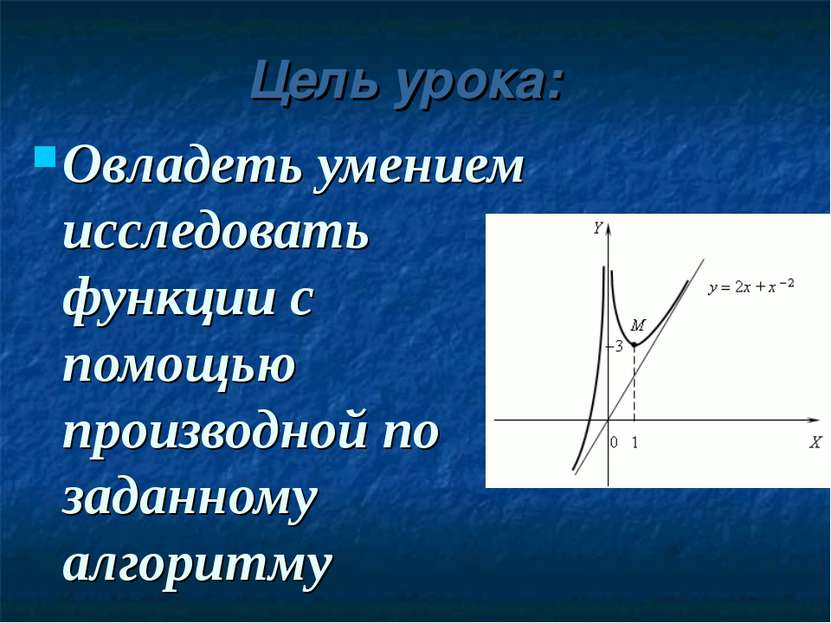
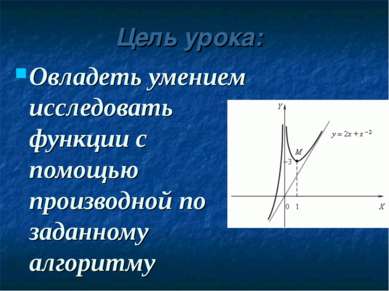Цель урока: Овладеть умением исследовать функции с помощью производной по заданному алгоритму
Cлайд 19
Диктант
Cлайд 20
Ответы на диктант
Cлайд 21
Подумай и ответь Сформулировать достаточные условия возрастания(убывания) функции.
Cлайд 22
Подумай и ответь Какие точки называются критическими ?
Cлайд 23
Подумай и ответь Сформулировать достаточный и необходимый признаки существования максимума(минимума) функции
Cлайд 24
«Спорьте, заблуждайтесь, ошибайтесь, но, ради Бога размышляйте, и, хотя криво – да сами , ». Г. Лессинг.
Cлайд 25
Cлайд 26
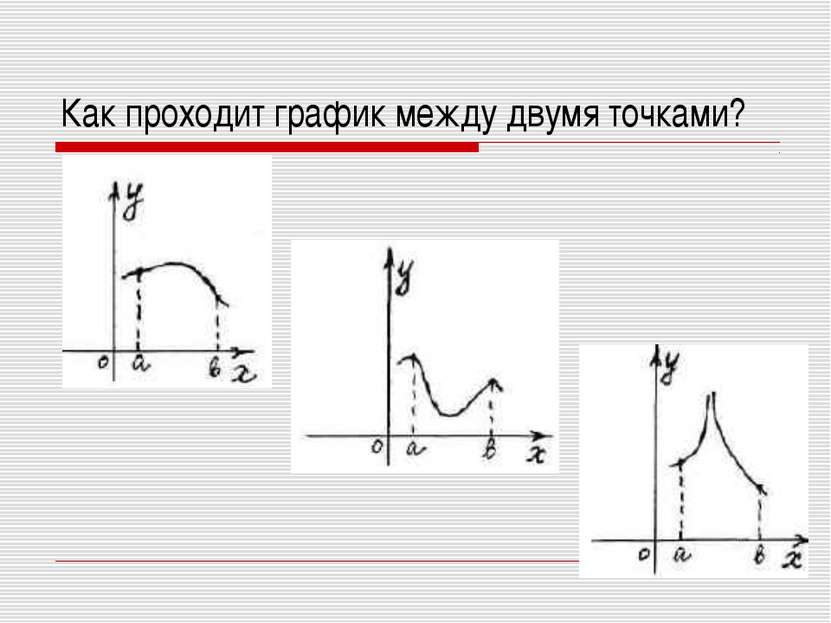
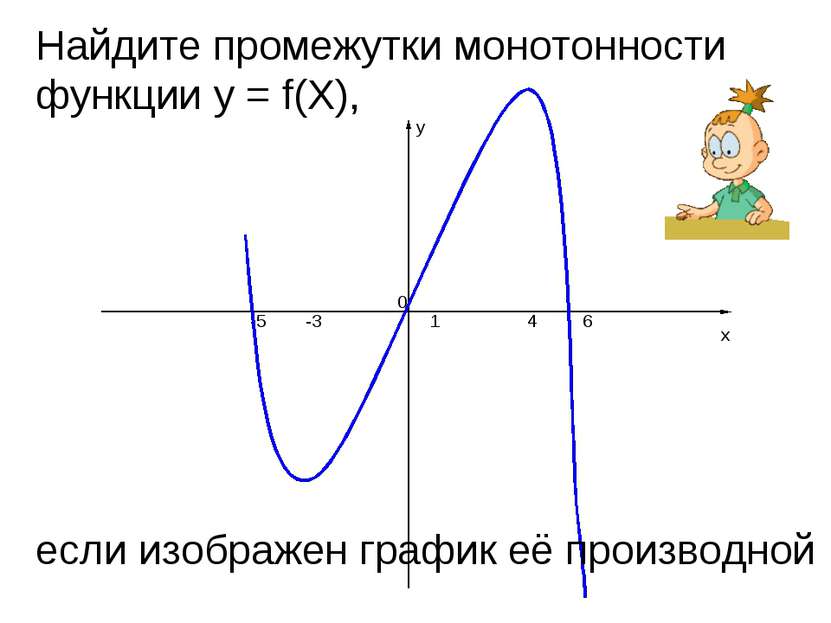
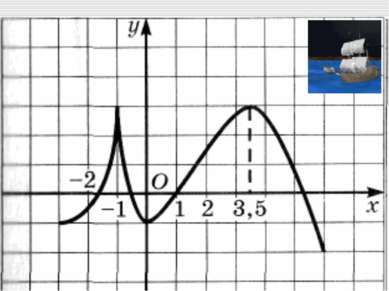
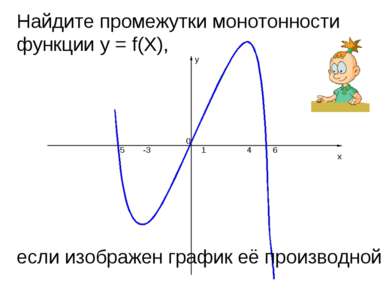y x 4 1 -3 -5 6 0 Найдите промежутки монотонности функции y = f(X), если изображен график её производной
Cлайд 27
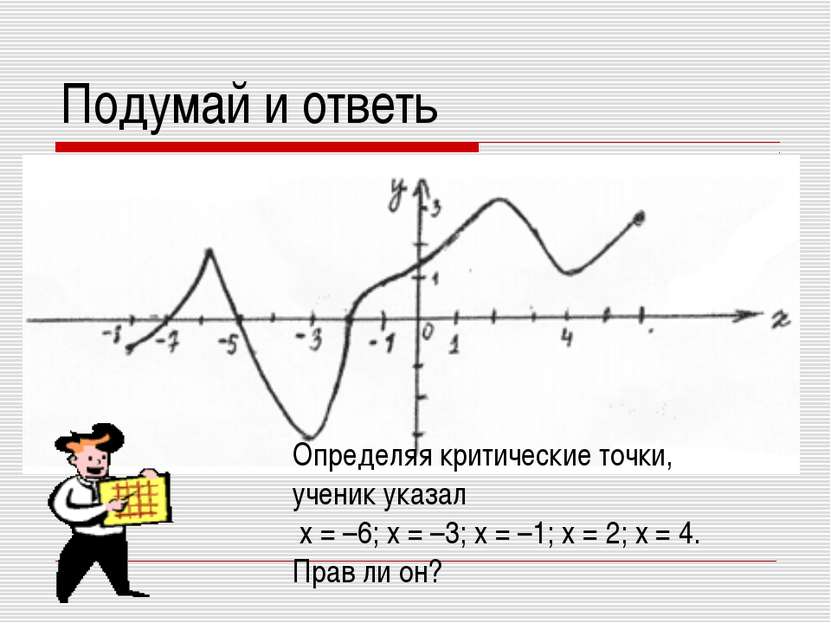
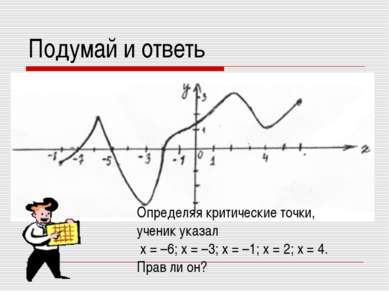Подумай и ответь Определяя критические точки, ученик указал x = –6; x = –3; x = –1; x = 2; x = 4. Прав ли он?
Cлайд 28
Схема исследования функции Найти область определения функции. Определить четность и нечетность, периодичность функции. Найти точки пересечения графика функции с осями координат. Определить промежутки знакопостоянства функции. Определить промежутки возрастания, убывания, найти экстремумы. На основании исследования построить график функции.
Cлайд 29
Схема исследования функции с помощью её производной Найти область определения функции. Определить четность и нечетность, периодичность функции. Найти точки пересечения графика функции с осями координат. Определить промежутки знакопостоянства функции.
Cлайд 30
5) Найти производную функции f′(х), найти критические точки - решить уравнение f′(х)=0. 6) Найти промежутки возрастания, убывания функции - решить неравенства f′(х)0. Определить экстремумы функции. 7)На основании исследования построить график функции.
Cлайд 31
Скажи мне, я забуду. Покажи мне, и, может быть, я буду помнить. Позволь мне сделать это, и это станет моим навсегда. (Китайская пословица)
Cлайд 32
Какой из графиков наиболее точно отражает описанную ситуацию?
Cлайд 33
Опишите динамику производительности труда рабочего, пользуясь ее графиком 8
Cлайд 34
Реклама Изучение производных поможет Вам быстро и правильно принимать решения в различных ситуациях, так как Вы уже учитесь думать, преодолевать трудности и рассуждать, а это всё ведет к приобретению мудрости.
Cлайд 35
«Ситуации в жизни бывают такие: либо сложные, либо простые…»
Cлайд 36
Домашнее задание Исследовать функцию и построить гафик f(x)= 2x²+5x+2
Cлайд 37
Вывод Аппарат производной можно использовать при решении геометрических задач, задач из естественных и гуманитарных наук, экономических задач. И, конечно, не обойтись без производной при исследовании функции и построении графиков.
Cлайд 38
Cлайд 39
