X
Код презентации скопируйте его
Вписанная и описанная окружность
Скачать эту презентацию
Презентация на тему Вписанная и описанная окружность
Скачать эту презентациюCлайд 1
Решение задач по теме «Вписанная и описанная окружность»(8кл) МОБУ « Новочеркасская СОШ» Булдакова Л.П
Cлайд 2
Цели и задачи урока Учить применять свойства вписанной и описанной окружности при решении задач; Развивать самостоятельность, логически мыслить и правильно выражать свои мысли;
Cлайд 3
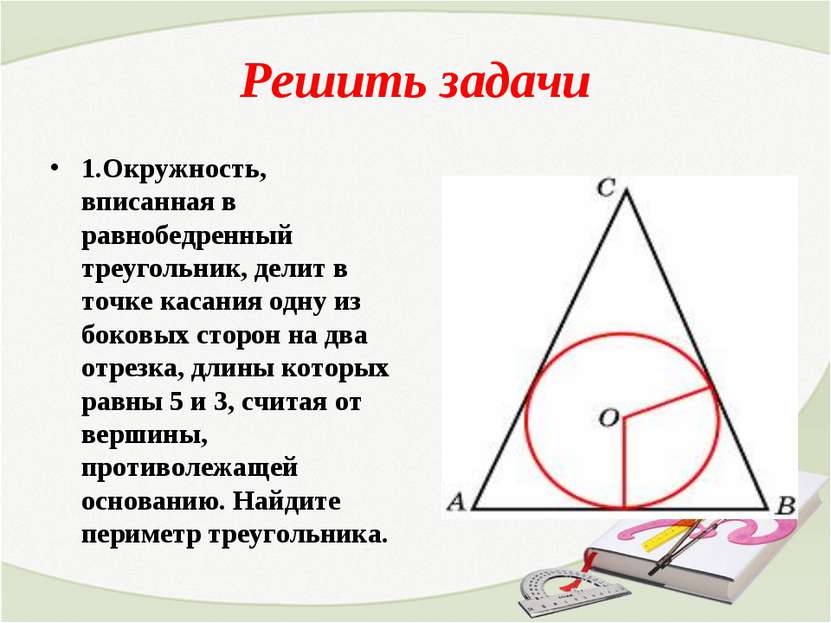
Решить задачи 1.Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Cлайд 4
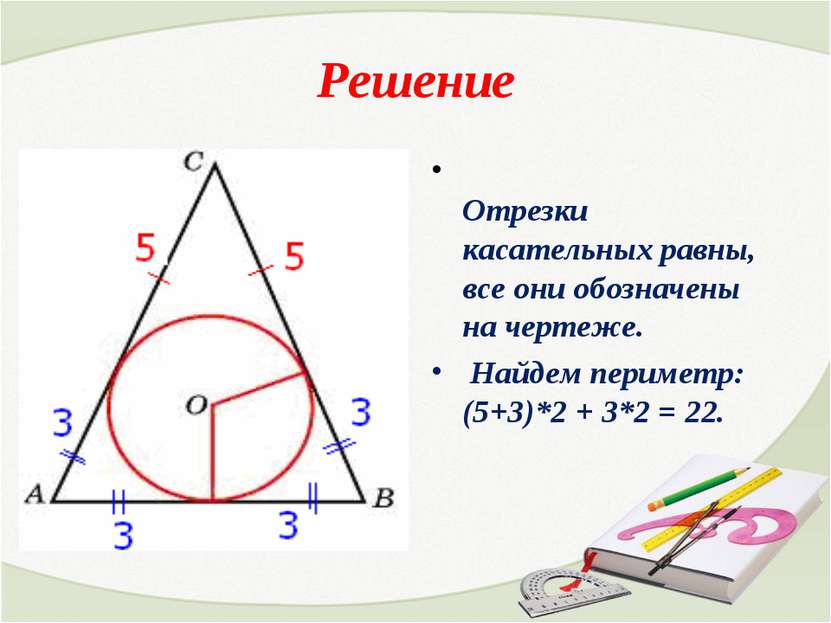
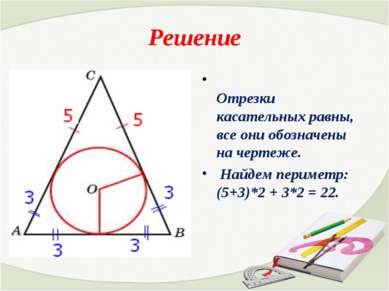Решение Отрезки касательных равны, все они обозначены на чертеже. Найдем периметр: (5+3)*2 + 3*2 = 22.
Cлайд 5
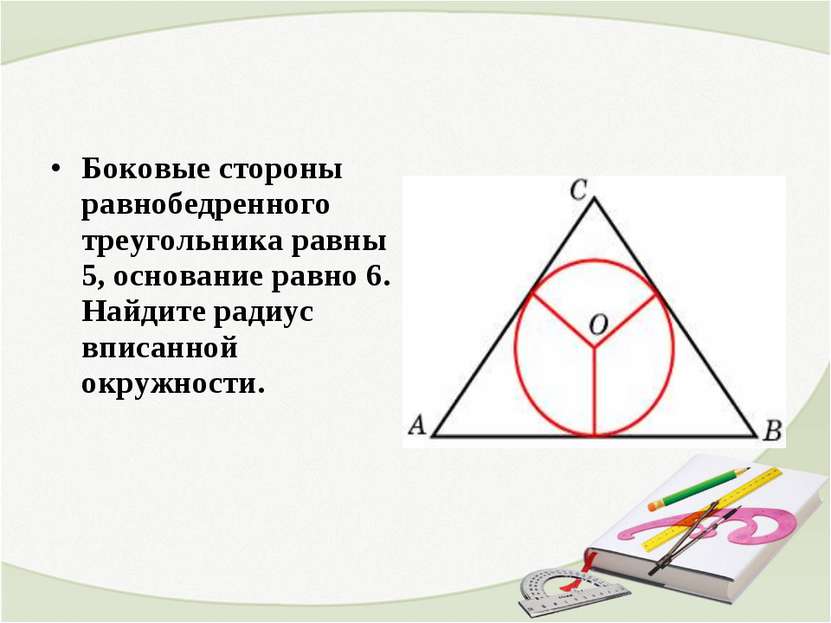
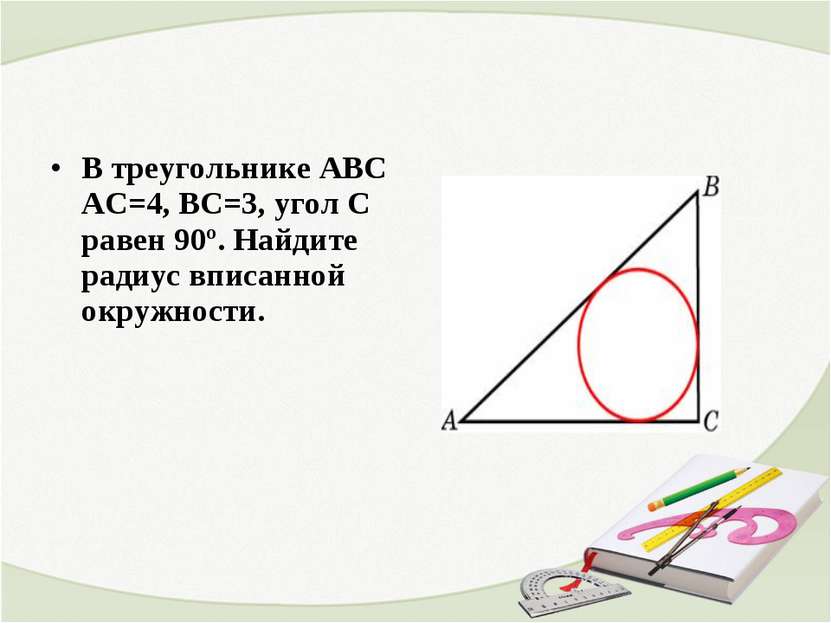
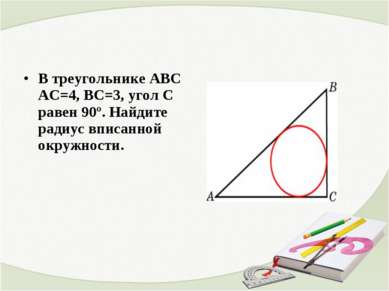
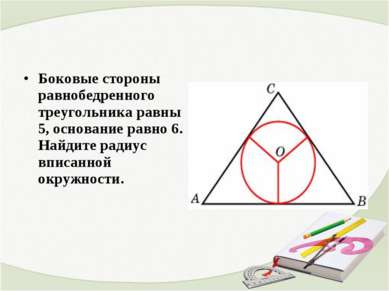Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
Cлайд 6
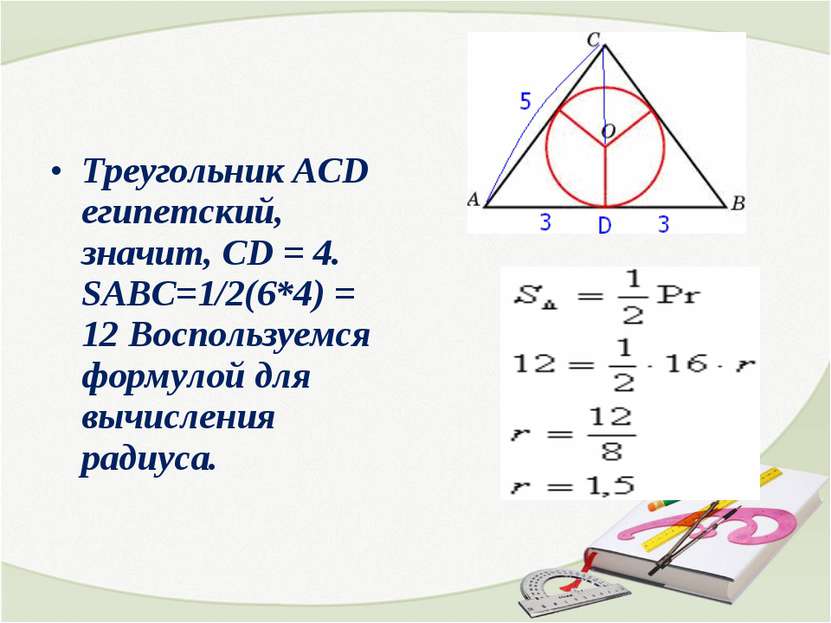
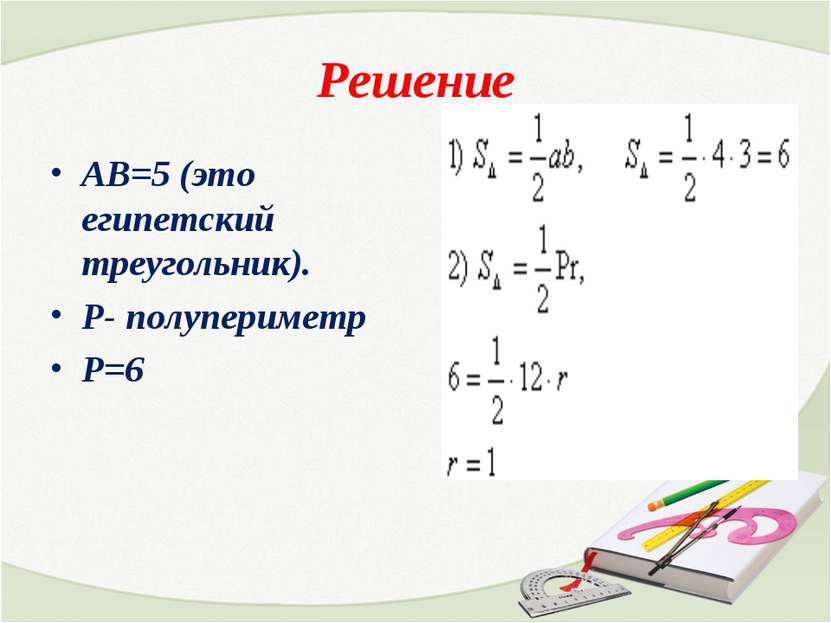
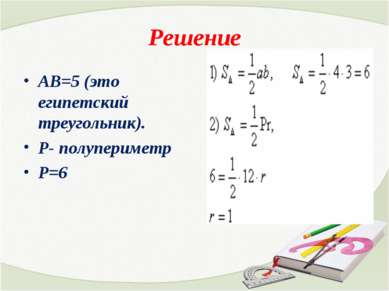
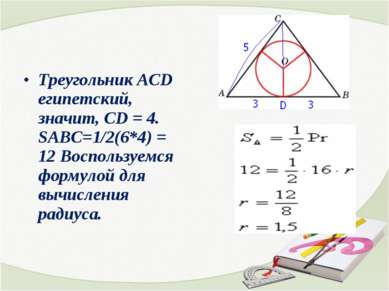Треугольник АСD египетский, значит, СD = 4. SABC=1/2(6*4) = 12 Воспользуемся формулой для вычисления радиуса.
Cлайд 7
В треугольнике ABC АС=4, ВС=3, угол C равен 90º. Найдите радиус вписанной окружности.
Cлайд 8
Решение АВ=5 (это египетский треугольник). Р- полупериметр Р=6
Cлайд 9
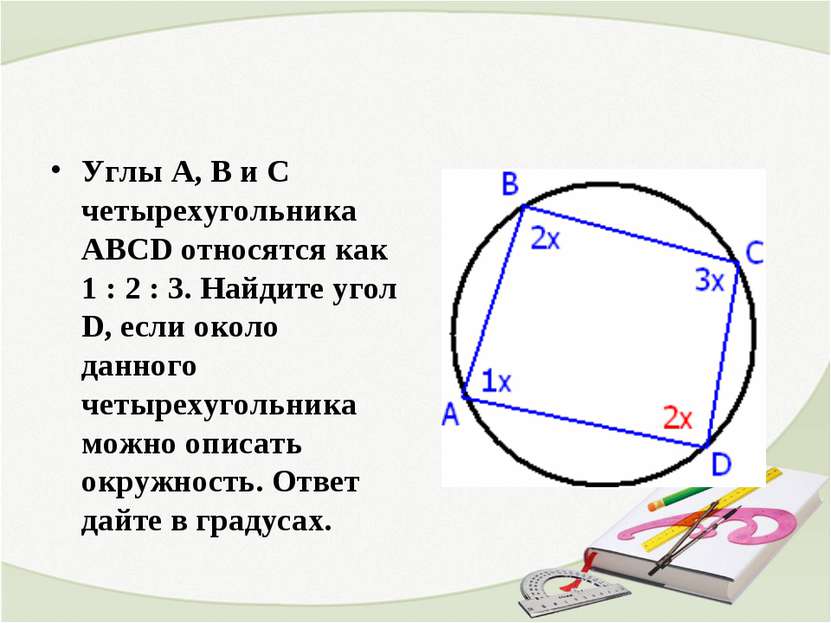
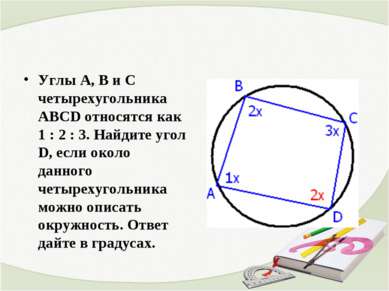Углы А, В и С четырехугольника ABCD относятся как 1 : 2 : 3. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
Cлайд 10
Решение Пусть углы 1х, 2х, 3х. По условию около данного четырехугольника можно описать окружность А+С = D+B. Тогда угол D=2х. Сумма противоположных углов описанного четырехугольника 180. 1х+3х=180 (или 2х+2х=180) х=45 (1 часть) Угол D=90
Cлайд 11
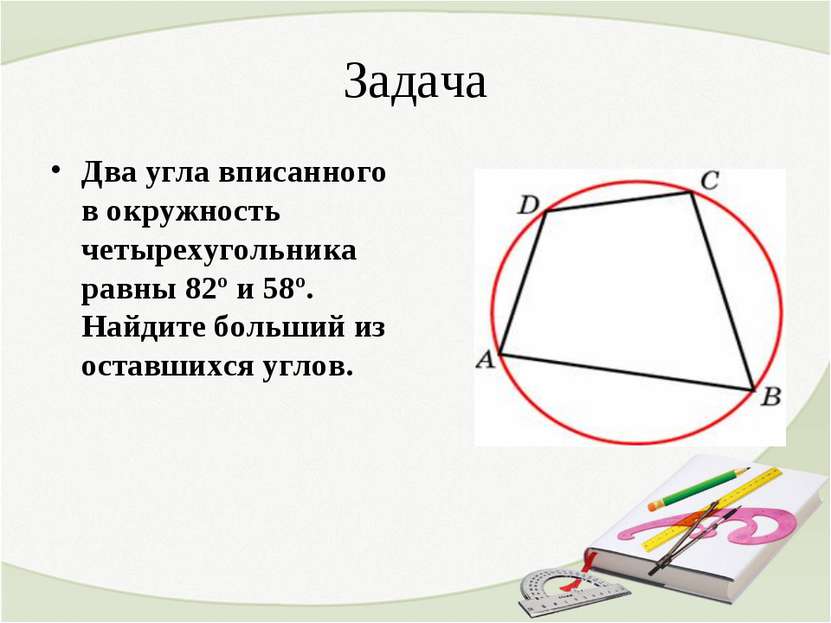
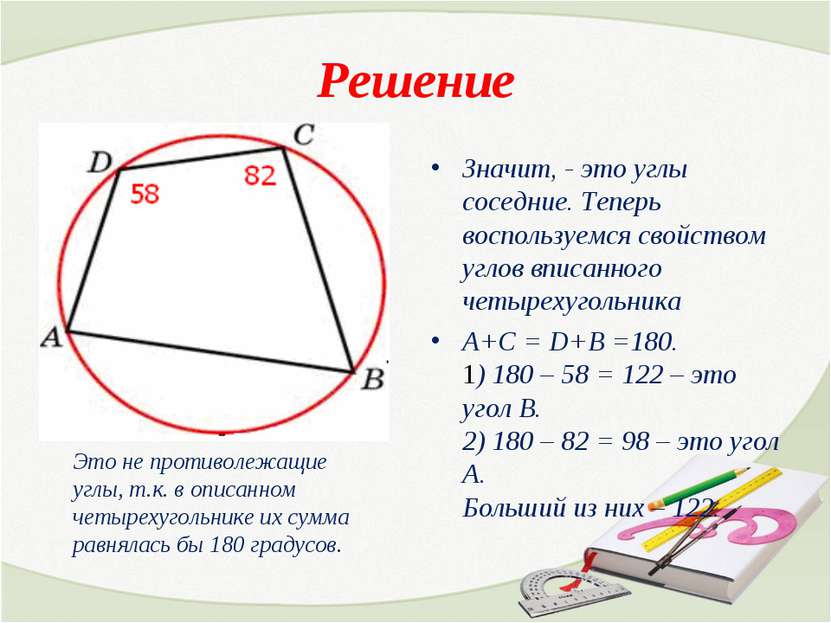
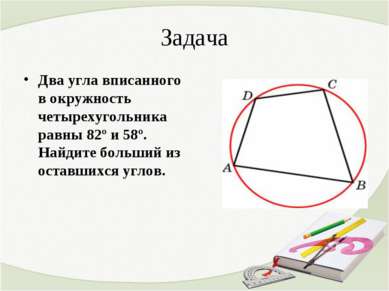Задача Два угла вписанного в окружность четырехугольника равны 82º и 58º. Найдите больший из оставшихся углов.
Cлайд 12
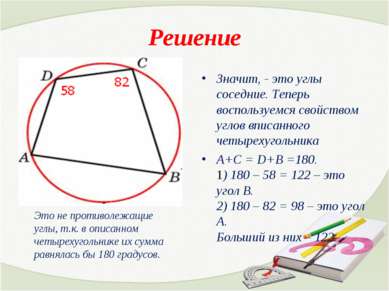Решение Значит, - это углы соседние. Теперь воспользуемся свойством углов вписанного четырехугольника А+С = D+B =180. 1) 180 – 58 = 122 – это угол В. 2) 180 – 82 = 98 – это угол А. Больший из них – 122. Это не противолежащие углы, т.к. в описанном четырехугольнике их сумма равнялась бы 180 градусов.
Cлайд 13
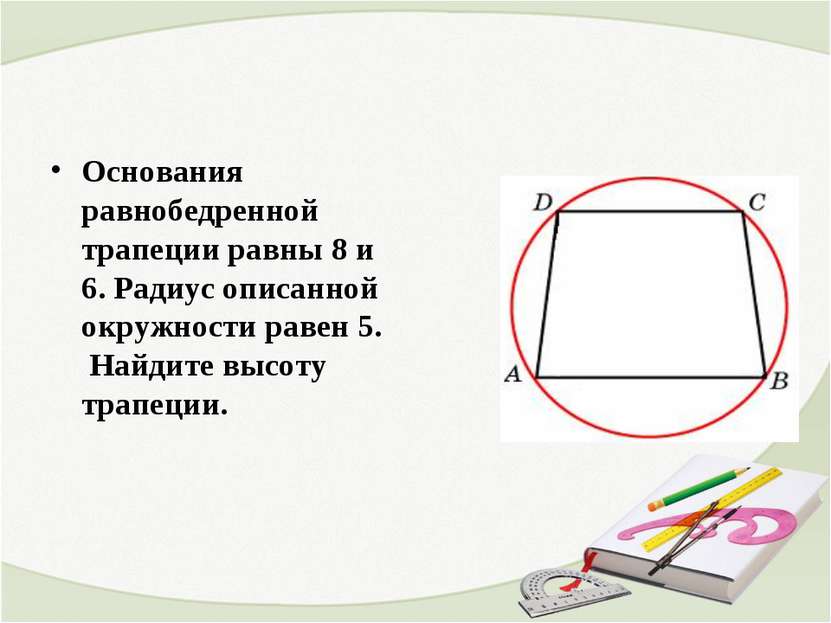
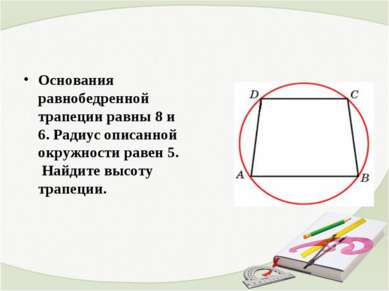Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Cлайд 14
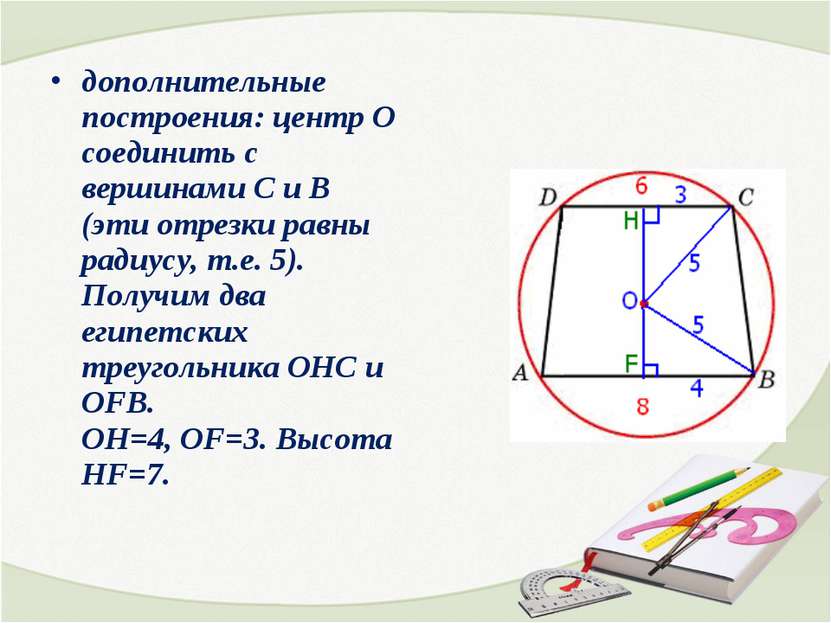
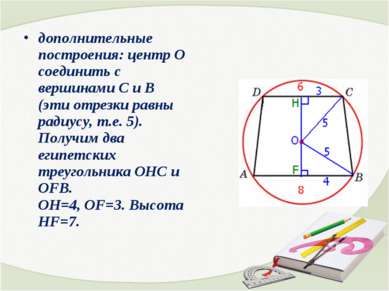дополнительные построения: центр О соединить с вершинами С и В (эти отрезки равны радиусу, т.е. 5). Получим два египетских треугольника ОHC и OFB. ОH=4, OF=3. Высота HF=7.
Cлайд 15
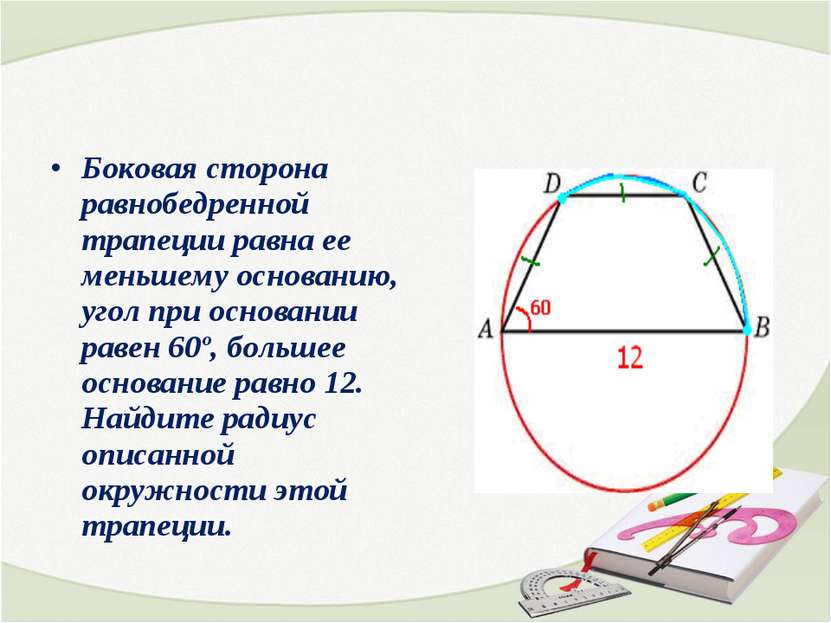
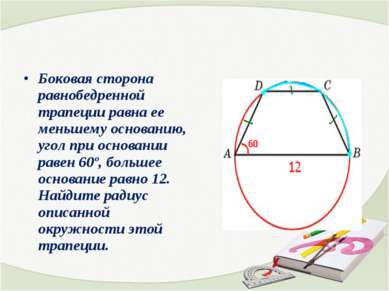Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60º, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Cлайд 16
Решение Вписанный угол ВАD опирается на дугу DCB. дуга DCB=120, а дуга DC = 60. Три дуги стягивают равные хорды AD, DC, CB. Они равны 60. Тогда дуга AB= 180. а это означает, что АВ – диаметр, тогда радиус 12:2 = 6.
Cлайд 17
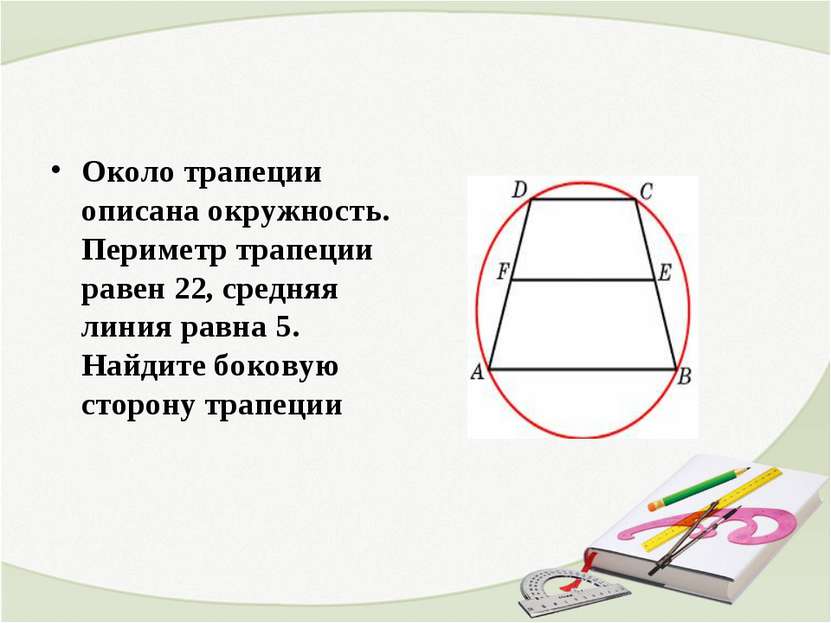
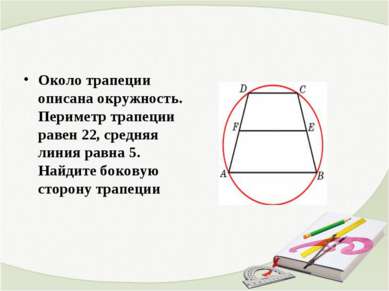Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции
Cлайд 18
Решение 1) Средняя линия равна полусумме оснований. Тогда сумма оснований равна 10. 2) 22 – 10 = 12 это приходиться на боковые стороны. 3) 12:2 = 6, боковые стороны вписанной трапеции равны.
Cлайд 19
Интернет-ресурсы Книга: http://www.liveinternet.ru/users/4321745/post201324261/ Карандаш: http://allforchildren.ru/pictures/showimg/school5/school0519jpg.htm Линейка, циркуль, лекало: http://www.ineedsex.ru/main.php?g2_view=core.DownloadItem&g2_itemId=345&g2_serialNumber=2 Транспортир: http://knopka48.ru/images/detailed/1/26449_2.png
Cлайд 20
Автор шаблона: Ранько Елена Алексеевна учитель начальных классов МАОУ лицей №21 г. Иваново Сайт: http://pedsovet.su/
