X
Код презентации скопируйте его
Алгоритмы внутренних точек с приближенным решением вспомогательной задачи
Скачать эту презентацию
Презентация на тему Алгоритмы внутренних точек с приближенным решением вспомогательной задачи
Скачать эту презентациюCлайд 1
Алгоритмы внутренних точек с приближенным решением вспомогательной задачи Филатов А.Ю. к.ф.-м.н., ИСЭМ СО РАН, ИГУ (Иркутск) Пержабинский С.М. ИСЭМ СО РАН (Иркутск) Работа выполнена при финансовой поддержке РФФИ (проект 05-01-00587а) http://polnolunie.baikal.ru/me/mat_prog.htm, http://matec.isu.ru
Cлайд 2
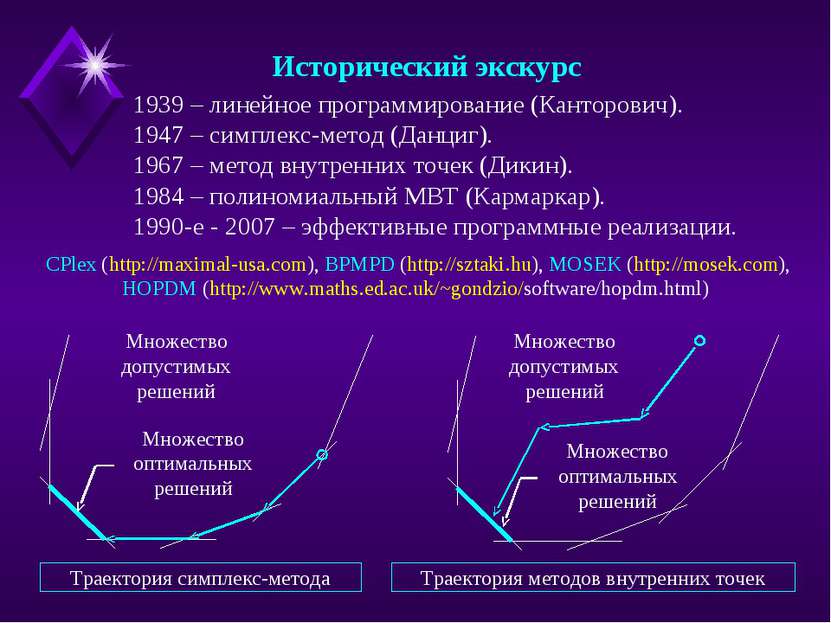
1939 – линейное программирование (Канторович). 1947 – симплекс-метод (Данциг). 1967 – метод внутренних точек (Дикин). 1984 – полиномиальный МВТ (Кармаркар). 1990-е - 2007 – эффективные программные реализации. CPlex (http://maximal-usa.com), BPMPD (http://sztaki.hu), MOSEK (http://mosek.com), HOPDM (http://www.maths.ed.ac.uk/~gondzio/software/hopdm.html) Исторический экскурс
Cлайд 3
Основные классы алгоритмов внутренних точек (1) (2) Пара взаимно-двойственных задач линейного программирования Аффинно-масштабирующие алгоритмы. Алгоритмы центрального пути. Алгоритмы скошенного пути. Комбинированные алгоритмы. Прямые алгоритмы. Двойственные алгоритмы. Прямо-двойственные алгоритмы.
Cлайд 4
Аффинно-масштабирующие алгоритмы внутренних точек Стартовое приближение: Итеративный переход: Задача поиска направления корректировки: Шаг корректировки: (3) Способы выбора весовых коэффициентов: (4) (5) (6) (7)
Cлайд 5
Алгоритмы центрального пути (имеют полиномиальные оценки) Логарифмическая барьерная функция: (8) Задача поиска направления корректировки: Комбинированные алгоритмы (используют параметризацию) (10) (9) Задача поиска направления корректировки:
Cлайд 6
Решение вспомогательной задачи Аффинно-масштабирующие алгоритмы: Алгоритмы центрального пути: Комбинированные алгоритмы: (11) (12) (13) (14) (17) (18) (15) (16)
Cлайд 7
Методы решения вспомогательной задачи Метод Гаусса. Метод Халецкого (метод квадратного корня). Метод сопряженных направлений. Метод Зейделя. Другие приближенные итеративные методы. Предпосылки использования приближенных итеративных методов На первых итерациях достаточно искать приближенное направление корректировки , используя вектор , для которого . В финале вычислительного процесса, диагональная мат- рица изменяется по итерациям очень незначительно, имеется хорошее стартовое приближение .
Cлайд 8
Метод сопряженных направлений Направление корректировки: Шаг, определяющий вариант метода: Итеративный переход: Шаг корректировки:
Cлайд 9
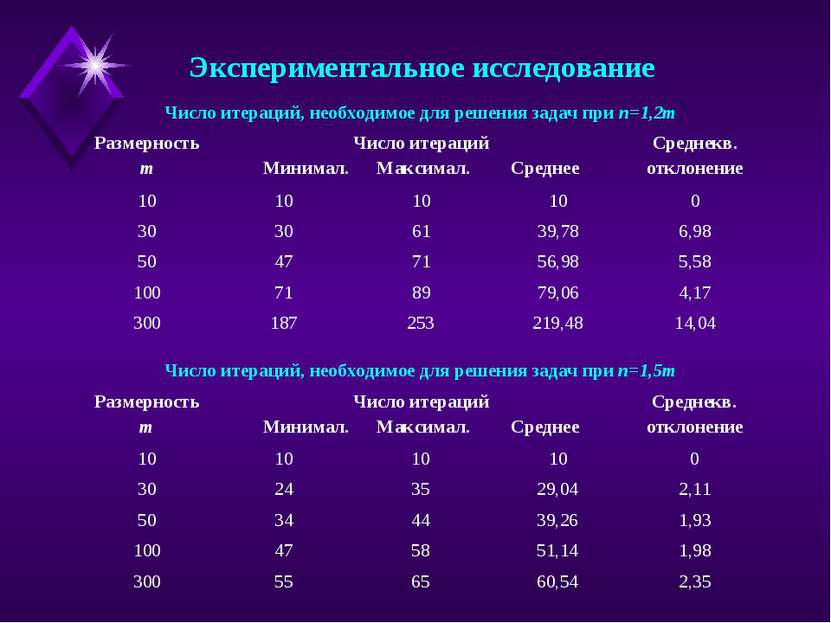
Экспериментальное исследование Число итераций, необходимое для решения задач при n=1,2m Число итераций, необходимое для решения задач при n=1,5m Размерность m Число итераций Минимал. Максимал. Среднее Среднекв. отклонение 10 10 10 10 0 30 30 61 39,78 6,98 50 47 71 56,98 5,58 100 71 89 79,06 4,17 300 187 253 219,48 14,04 Размерность m Число итераций Минимал. Максимал. Среднее Среднекв. отклонение 10 10 10 10 0 30 24 35 29,04 2,11 50 34 44 39,26 1,93 100 47 58 51,14 1,98 300 55 65 60,54 2,35
Cлайд 10
Параметры управления алгоритмом Вариант приближенного метода. – параметр в условии останова δ – параметр в условие перехода с точного на приближенный метод K – максимальное число выполняемых подряд итераций приближенного метода. t – число внутренних итераций приближенного метода. Процедуры корректировки формул (3), (10) и формул вычисления максимального шага на фазе 1. – прогноз шага корректировки.
Cлайд 11
Спасибо за внимание!
