X
Код презентации скопируйте его
Особенности геометрических построений на компьютере
Скачать эту презентацию
Презентация на тему Особенности геометрических построений на компьютере
Скачать эту презентациюCлайд 1
Автор: Виноградов Никита, ученик 9 класса, МКОУ Плесской средней общеобразовательной школы, обучающийся объединения «Программирование» МКОУ ДОД ЦДЮТ Руководитель: Юдин Андрей Борисович, учитель математики МКОУ Плесской средней общеобразовательной школы, педагог дополнительного образования МКОУ ДОД ЦДЮТ Плес. 2013 год.
Cлайд 2
Выяснить какие знания из курса алгебры и геометрии требуются для решения задач на построение геометрических фигур на компьютере, и разработать алгоритмы для решения задач на построение. Ц Е Л Ь Р А Б О Т Ы
Cлайд 3
З А Д А Ч И Ознакомится с теорией построений изображений на компьютере при помощи «базовой точки». Найти необходимые формулы для построения геометрических фигур. Реализовать полученные алгоритмы в системе программирования PascalABC. Составить «сборник» использованных мною формул, определений и теорем.
Cлайд 4
Поисковый метод с использованием научной и учебной литературы. Практический метод составления алгоритмов решения задач, и их реализация в системе программирования PascalABC. Исследовательский метод при выборе алгоритма решения задачи, и построении математической модели. Анализ полученных в ходе исследования данных М Е Т О Д Ы
Cлайд 5
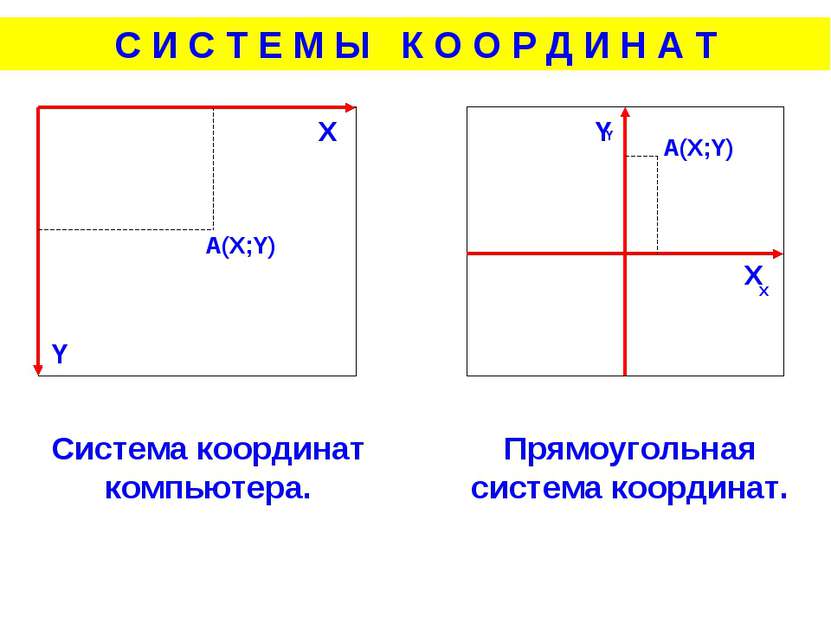
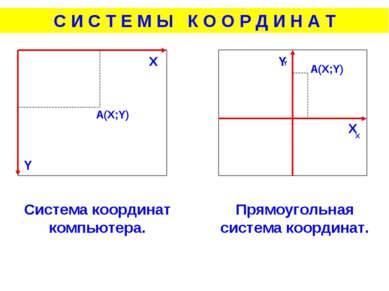A(X;Y) X Y X Y Система координат компьютера. Прямоугольная система координат. С И С Т Е М Ы К О О Р Д И Н А Т X Y A(X;Y)
Cлайд 6
М Е Т О Д Б А З О В О Й Т О Ч К И
Cлайд 7
Построение прямоугольного треугольника по двум катетам. Построение прямоугольного треугольника по катету и гипотенузе. Построение равностороннего треугольника. Построение треугольника по трем сторонам. Правильный шестиугольник Медиана к основанию и средняя линия треугольника. Построение трапеции по сторонам. Построение параллелограмма по двум сторонам и углу между ними. Построить вписанную в треугольник окружность Построить описанную вокруг треугольника окружность. З А Д А Ч И НА П О С Т Р О Е Н И Е
Cлайд 8
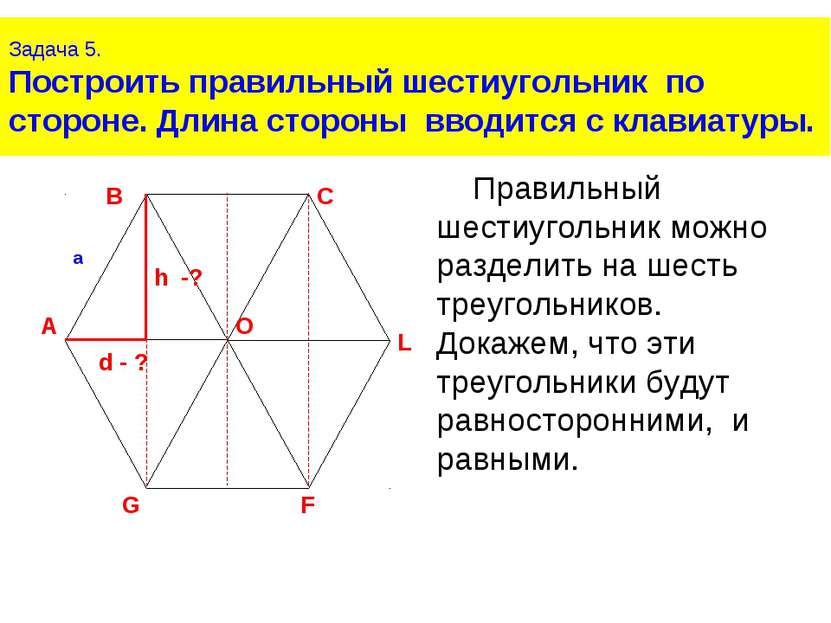
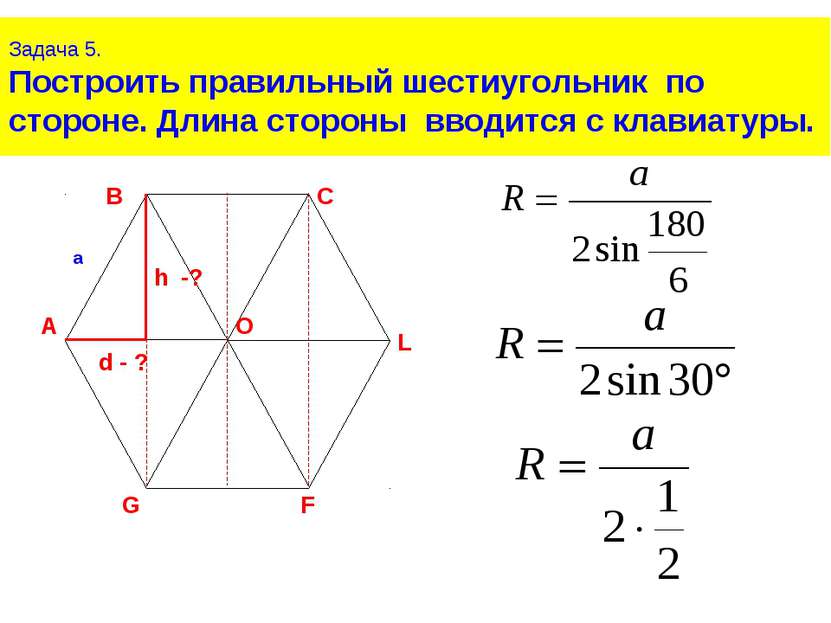
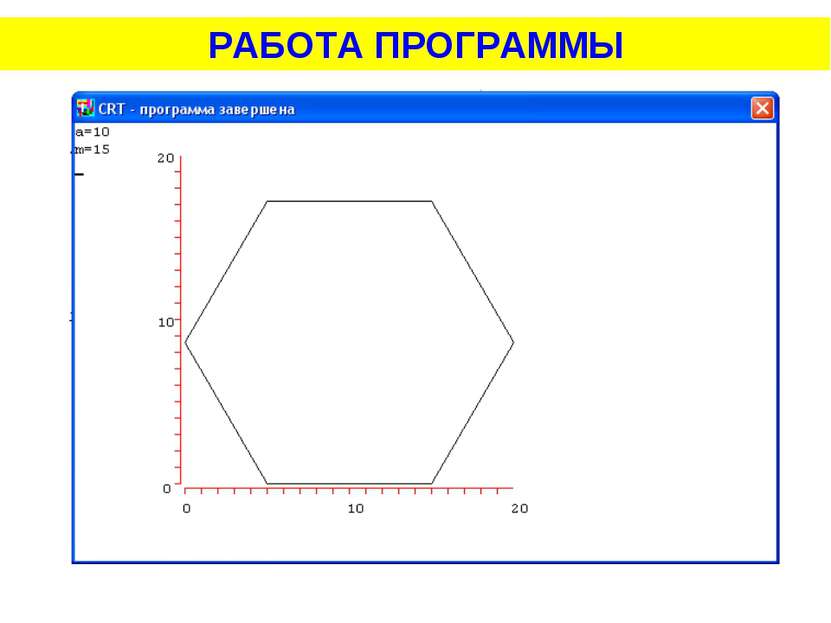
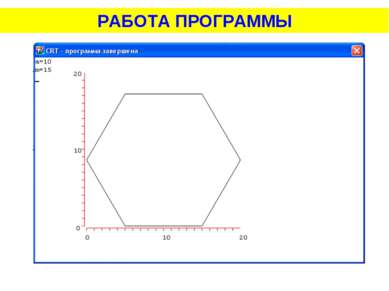
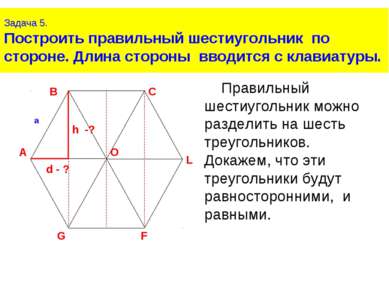Задача 5. Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры. Правильный шестиугольник можно разделить на шесть треугольников. Докажем, что эти треугольники будут равносторонними, и равными.
Cлайд 9
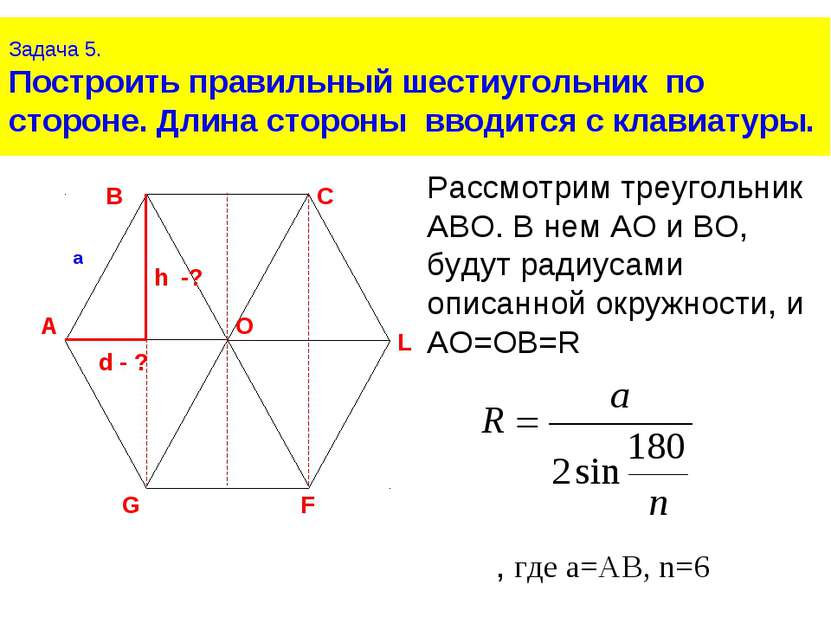
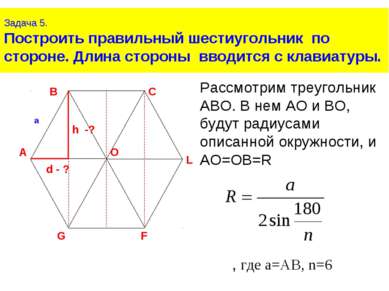Задача 5. Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры. Рассмотрим треугольник АВО. В нем АО и ВО, будут радиусами описанной окружности, и АО=ОВ=R , где a=AB, n=6
Cлайд 10
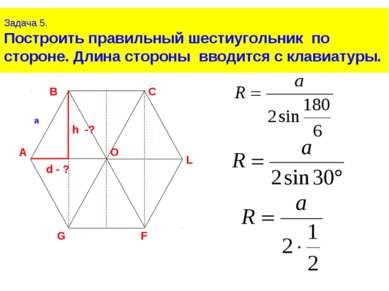Задача 5. Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры.
Cлайд 11
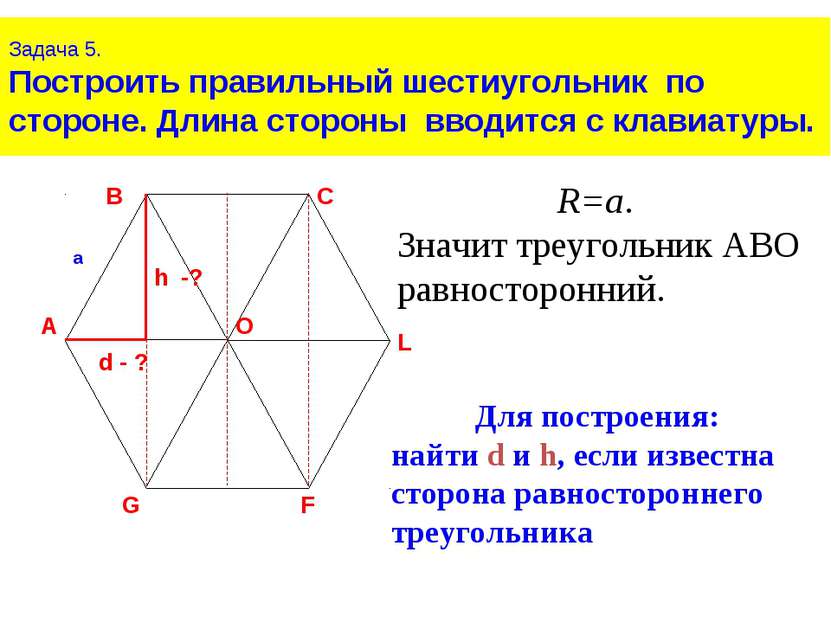
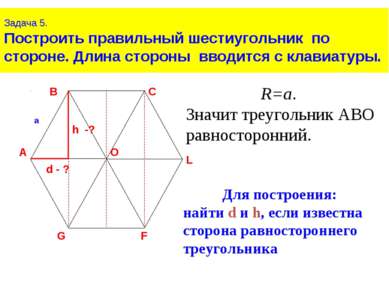Задача 5. Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры. R=a. Значит треугольник АВО равносторонний. Для построения: найти d и h, если известна сторона равностороннего треугольника
Cлайд 12
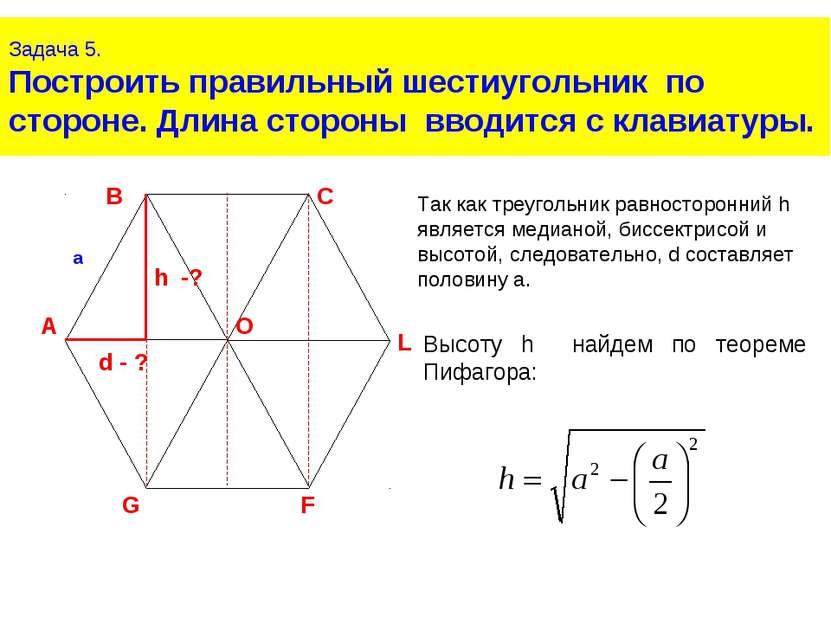
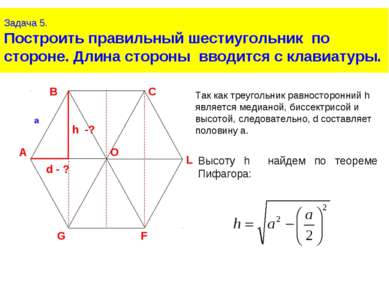Задача 5. Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры. Высоту h найдем по теореме Пифагора: Так как треугольник равносторонний h является медианой, биссектрисой и высотой, следовательно, d составляет половину a.
Cлайд 13
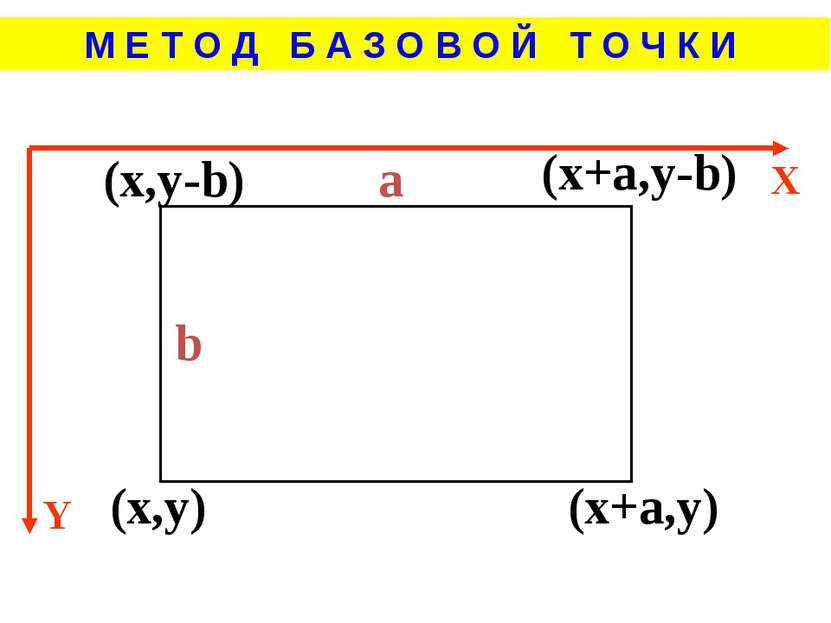
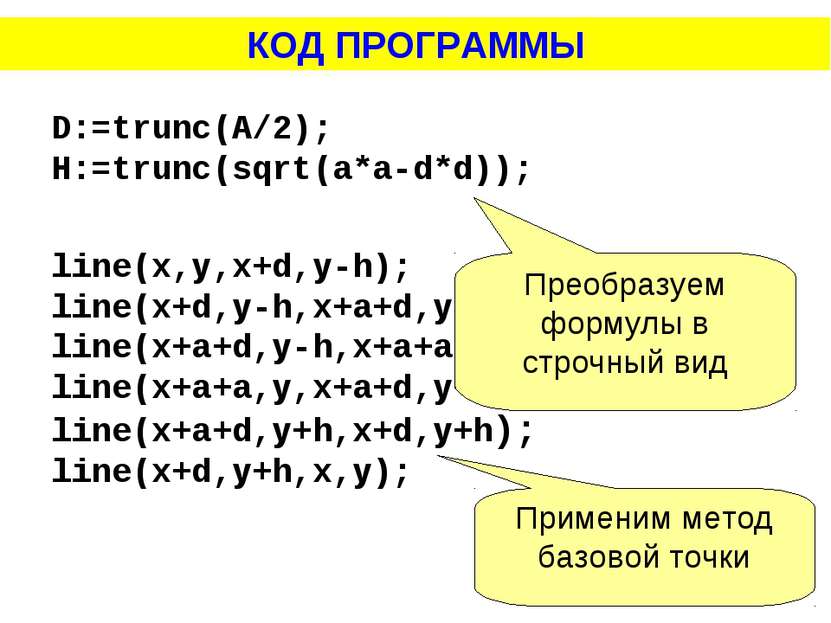
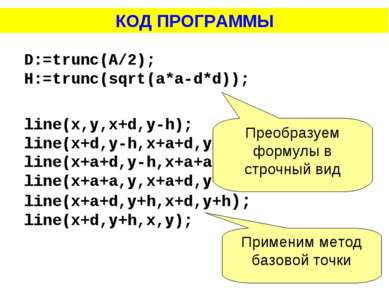D:=trunc(A/2); H:=trunc(sqrt(a*a-d*d)); line(x,y,x+d,y-h); line(x+d,y-h,x+a+d,y-h); line(x+a+d,y-h,x+a+a,y); line(x+a+a,y,x+a+d,y+h); line(x+a+d,y+h,x+d,y+h); line(x+d,y+h,x,y); КОД ПРОГРАММЫ Преобразуем формулы в строчный вид Применим метод базовой точки
Cлайд 14
РАБОТА ПРОГРАММЫ
Cлайд 15
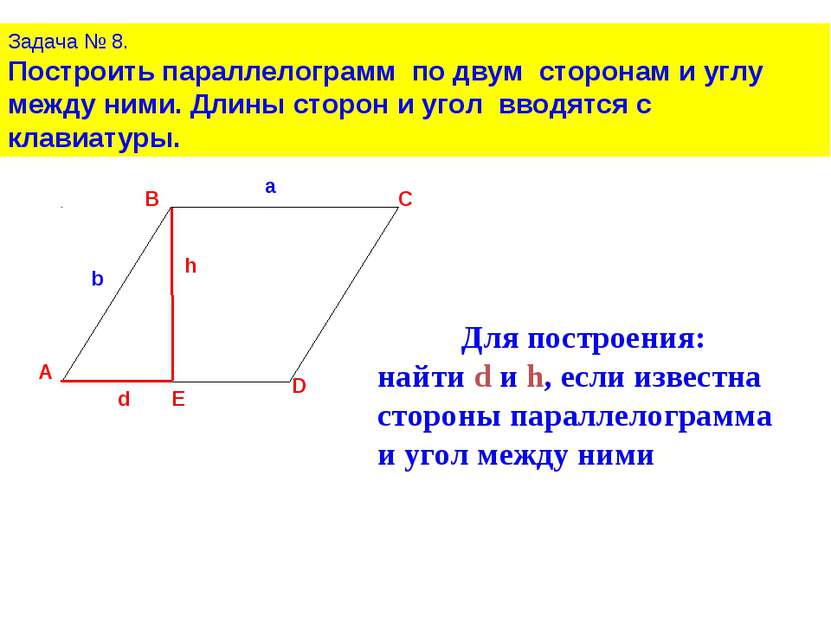
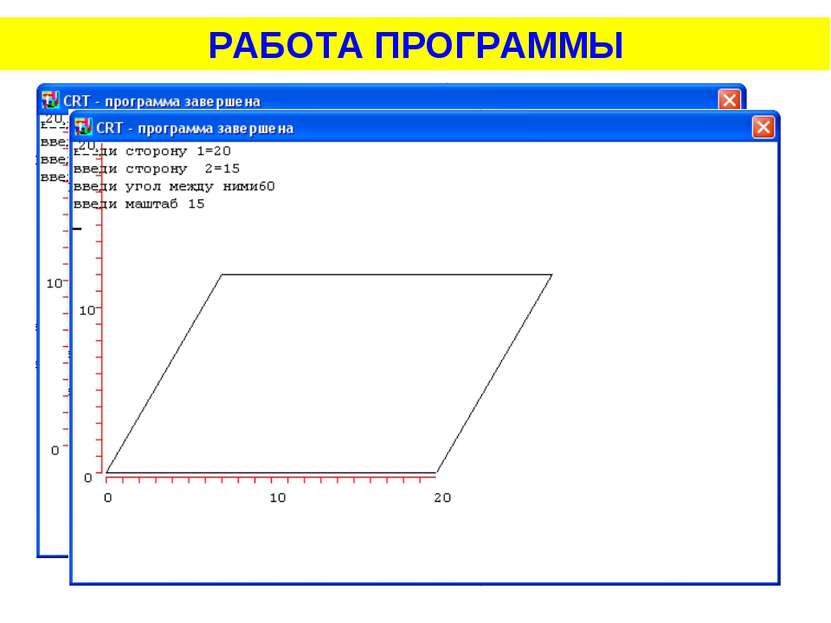
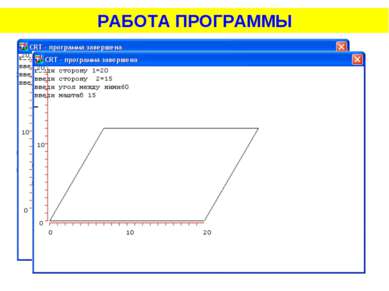
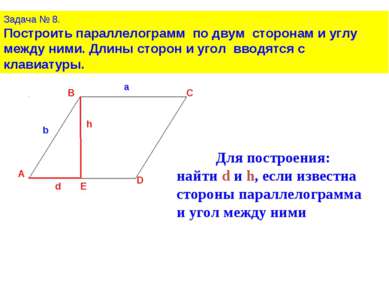Задача № 8. Построить параллелограмм по двум сторонам и углу между ними. Длины сторон и угол вводятся с клавиатуры. Для построения: найти d и h, если известна стороны параллелограмма и угол между ними
Cлайд 16
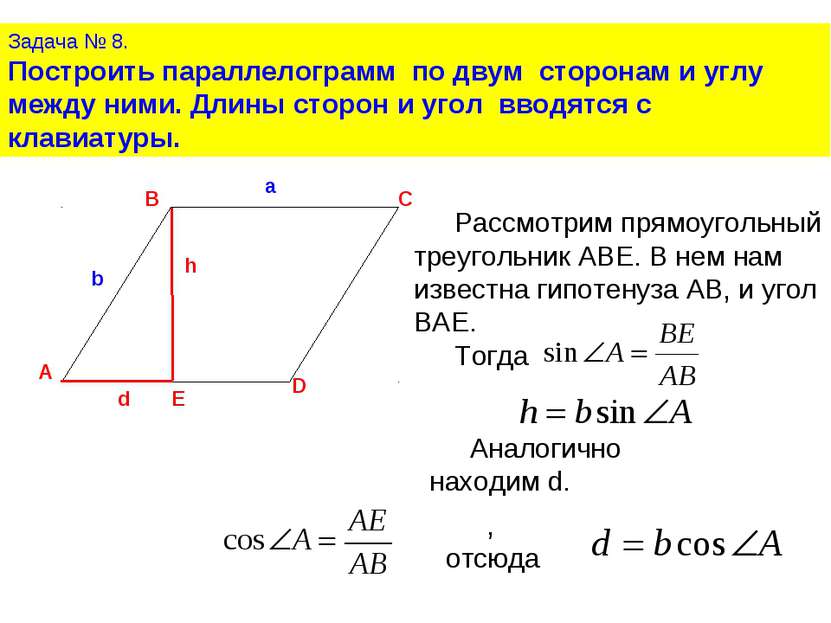
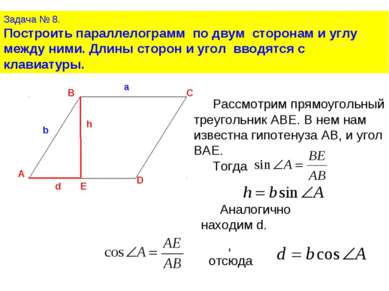Задача № 8. Построить параллелограмм по двум сторонам и углу между ними. Длины сторон и угол вводятся с клавиатуры. Рассмотрим прямоугольный треугольник ABE. В нем нам известна гипотенуза АВ, и угол BAE. Тогда Аналогично находим d. , отсюда
Cлайд 17
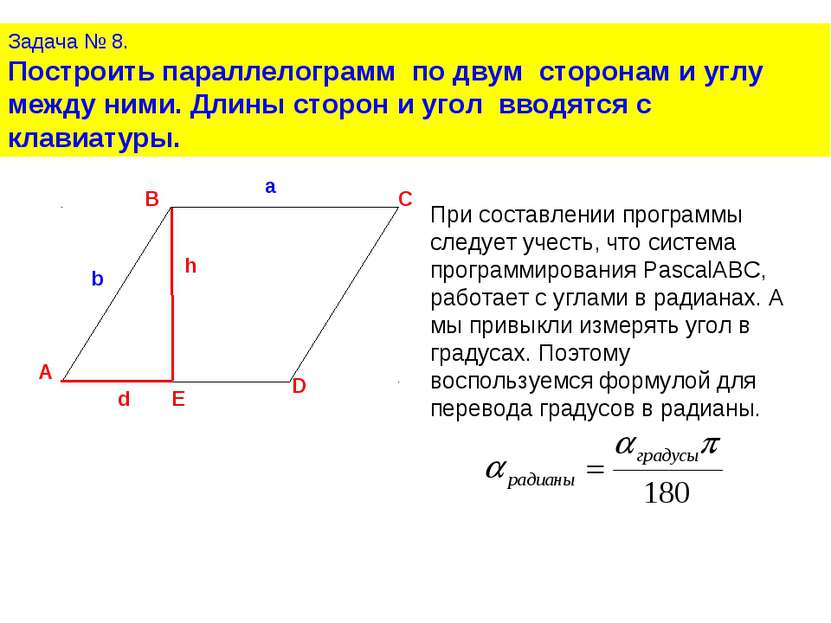
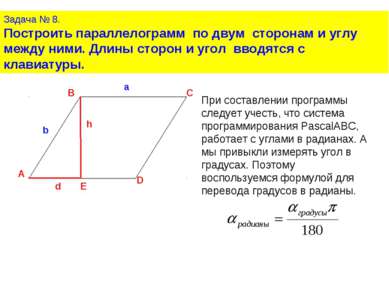Задача № 8. Построить параллелограмм по двум сторонам и углу между ними. Длины сторон и угол вводятся с клавиатуры. При составлении программы следует учесть, что система программирования PascalABC, работает с углами в радианах. А мы привыкли измерять угол в градусах. Поэтому воспользуемся формулой для перевода градусов в радианы.
Cлайд 18
КОД ПРОГРАММЫ Преобразуем формулы в строчный вид Применим метод базовой точки n:=(n*pi)/180; h:=trunc(b*sin(n)); d:=trunc(b*cos(n)); line(x,y,x+d,y-h); line(x,y,x+a,y); line(x+d,y-h,x+d+a,y-h); line(x+d+a,y-h,x+a,y);
Cлайд 19
РАБОТА ПРОГРАММЫ
Cлайд 20
Для решения этих задач мне потребовались следующие математические знания: Треуго льник— это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника.. Треугольник, у которого все стороны равны, называется равносторонним или правильным. Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами Теорема о медиане равнобедренного треугольника. Медиана, проведённая к основанию в равнобедренном треугольнике, является высотой и биссектрисой
Cлайд 21
Для решения этих задач мне потребовались следующие математические знания: Окружность называется описанной около треугольника, если она проходит через все его вершины. Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середину этих сторон Параллелограмм – четырёхугольник, у которого противолежащие стороны попарно параллельны, т.е. лежат на параллельных прямых. Противоположные стороны параллелограмма попарно равны. Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Синус угла - это отношение длины противоположного этому углу катета к гипотенузе Косинус угла - это отношение прилежащего этому углу катета к гипотенузе
Cлайд 22
Для решения этих задач мне потребовались следующие математические знания: Формула для перевода градусов в радианы Радиус окружности описанной вокруг правильного n угольника. … а для остальных задач, еще 31 правило и определение!
Cлайд 23
Проанализировав решенные мною задачи, я выписал те теоремы, определения и формулы из курса алгебры и геометрии 8 и 9 классов, которые были использованы при составлении этих 10 программ. Сами программы очень простые. В них реализован линейный алгоритм. Вся трудность заключалась в выводах формул, при помощи которых компьютер вычислял необходимые данные для построения геометрических фигур. В Ы В О Д
Cлайд 24
Программирование компьютерной графики невозможно без знания математики. Для построения геометрических фигур используется специальный метод, «базовой точки». З А К Л Ю Ч Е Н И Е
Cлайд 25
З А К Л Ю Ч Е Н И Е Александра Чигринец, на одном из форумов посвященных программированию сказал «…кроме того, математика формирует определённый склад мышления. Какой-то класс задач можно кодить без математики. Но в школе и институте закладывается база, фундамент. Чем фундамент основательнее, тем больше есть возможностей по возведению на нём чего-либо в будущем. Как говорил Абдула в "Белом солнце пустыни": "Хорошо тому, у кого есть кинжал. И плохо если его не окажется… в нужное время." Так вот запасаться кинжалом нужно заранее, а когда он понадобиться, то надо будет достать и пользоваться.»
