X
Код презентации скопируйте его
Решение логических задач
Скачать эту презентациюПрезентация на тему Решение логических задач
Скачать эту презентациюCлайд 2
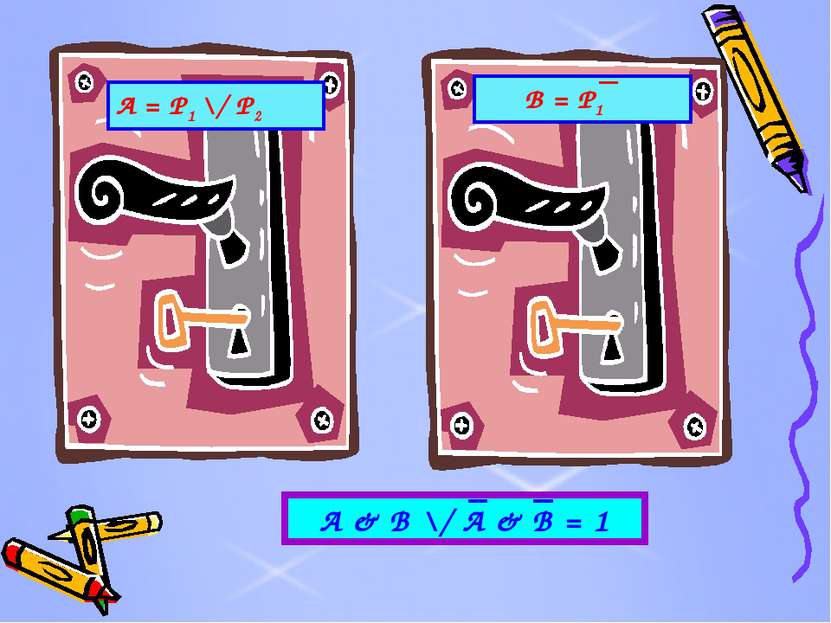
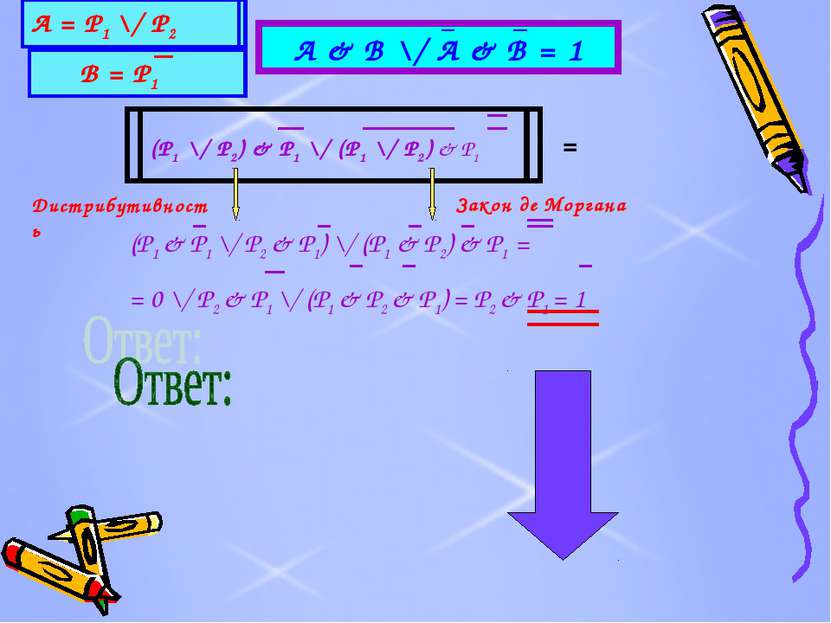
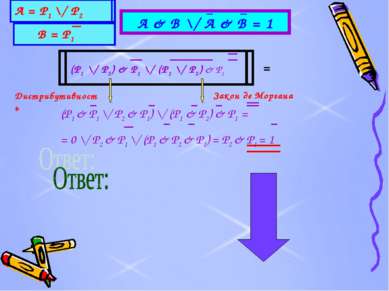
 Задача №1. В одном королевстве король всякому узнику, приговоренному к смерти, давал последний шанс спастись. Ему предлагалось угадать, в какой из двух комнат находится тигр, а в какой - принцесса. Хотя вполне могло быть, что король в обеих комнатах разместил принцесс или, что хуже, в обеих - тигров. Выбор надо сделать на основании табличек на дверях комнат. Причем узнику известно, что утверждения на табличках одновременно либо истины, либо ложны. Надписи были таковы. Первая комната: «По крайней мере, в одной из этих комнат находится принцесса». Вторая комната: «В другой комнате – тигр». Какую дверь должен выбрать узник?
Задача №1. В одном королевстве король всякому узнику, приговоренному к смерти, давал последний шанс спастись. Ему предлагалось угадать, в какой из двух комнат находится тигр, а в какой - принцесса. Хотя вполне могло быть, что король в обеих комнатах разместил принцесс или, что хуже, в обеих - тигров. Выбор надо сделать на основании табличек на дверях комнат. Причем узнику известно, что утверждения на табличках одновременно либо истины, либо ложны. Надписи были таковы. Первая комната: «По крайней мере, в одной из этих комнат находится принцесса». Вторая комната: «В другой комнате – тигр». Какую дверь должен выбрать узник?
Cлайд 3
 P1 = В первой комнате принцесса. P2 = Во второй комнате принцесса. P1 = В первой комнате тигр. P2 = Во второй комнате тигр.
P1 = В первой комнате принцесса. P2 = Во второй комнате принцесса. P1 = В первой комнате тигр. P2 = Во второй комнате тигр.