X
Код презентации скопируйте его
Формулы сокращенного умножения
Скачать эту презентацию
Презентация на тему Формулы сокращенного умножения
Скачать эту презентациюCлайд 1
Выполнила: учитель математики Захарченко Татьяна Николаевна МАОУ СОШ №17 г.Славянск-на-Кубани
Cлайд 2
(а + b)2 = а2 + 2аb + b2 (а – b)2 = а2 – 2аb + b2 а2 – b2 = (а – b) (а + b) а3 – b3 = (а – b )(а2 + аb + b2 ) а3 + b3 = ( а + b)(а2 – аb + b2 ) Вспомним:
Cлайд 3
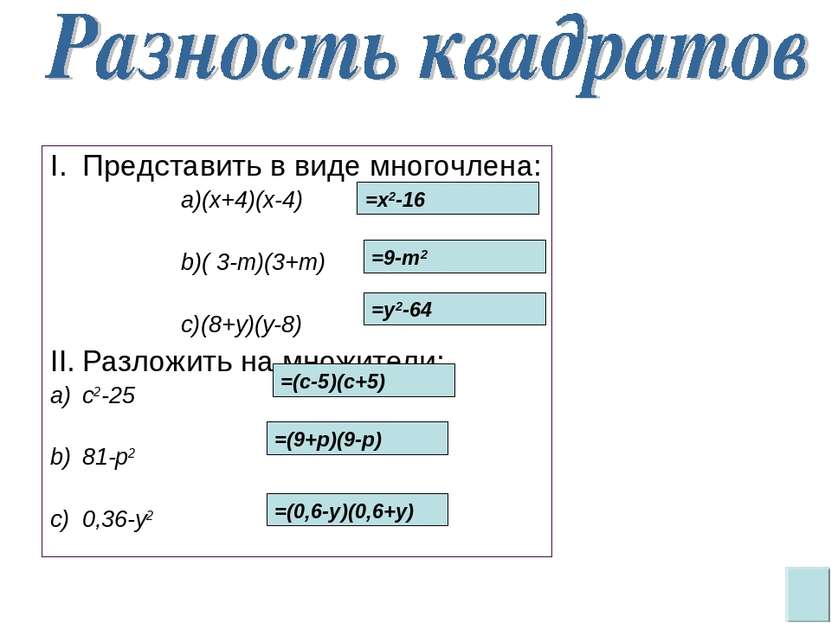
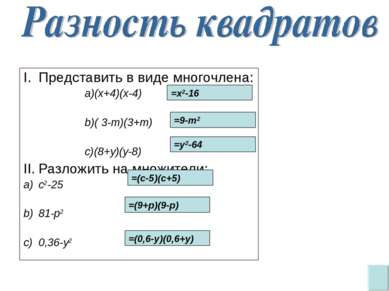Представить в виде многочлена: (x+4)(x-4) ( 3-m)(3+m) (8+y)(y-8) Разложить на множители: с2-25 81-p2 0,36-y2 =x2-16 =9-m2 =y2-64 =(с-5)(с+5) =(9+p)(9-p) =(0,6-y)(0,6+y)
Cлайд 4
Замени «звездочки»
Cлайд 5
Cлайд 6
Быстрый счёт А я догадался, как можно использовать эту формулу для быстрых вычислений. Смотри и учись. 292-282=(29-28)(29+28)=1*57=57 732-632=(73+63)(73-63)=136*10=1360 1332-1342=(133-134)(133+134)= -267
Cлайд 7
S-площадь квадрата со стороной a. По рисунку получаем S=S1+S2+2S3 таким образом, получаем a2=b2+(a-b)2+2(a-b)b a2-b2=(a-b)(a-b+2b) a2-b2=(a-b)(a+b) Доказательство: Доказано a2-b2=(a-b)(a+b)
Cлайд 8
Cлайд 9
Спасибо за внимание!
