X
Код презентации скопируйте его
Основы логики и логические основы построения компьютера
Скачать эту презентацию
Презентация на тему Основы логики и логические основы построения компьютера
Скачать эту презентациюCлайд 1
«Основы логики и логические основы построения компьютера» Из опыта работы Ермаковой В. В., учителя информатики МБОУ СОШ № 19 города Белово Кемеровской области
Cлайд 2
Процессор компьютера выполняет арифметические и логические операции над двоичными кодами. И поэтому чтобы иметь представление об устройстве компьютера, необходимо познакомиться с основными логическими элементами, лежащими в основе его построения. Для понимания принципа работы таких элементов изучим основные начальные понятия алгебры логики.
Cлайд 3
Логика - это наука о формах и способах мышления. Термин «логика» происходит от древнегреческого logos, означающего «слово, мысль, понятие, рассуждение, закон» Основными формами мышления являются понятие, высказывание и умозаключение.
Cлайд 4
Первые учения о формах и способах рассуждений возникли в странах Дальнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегреческими мыслителями. Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления от его содержания.
Cлайд 5
Алгебру логики так же называют алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения.
Cлайд 6
Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта. Понятие имеет две стороны: содержание и объём. Например, содержание понятия «персональный компьютер – это универсальное электронное устройство для автоматической обработки информации, предназначенное для одного пользователя.» Объём понятия «персональный компьютер» выражает всю совокупность существующих в настоящее время в мире персональных компьютеров. Форма мышления
Cлайд 7
Высказывание (суждение) – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов, их свойствах и отношениях между ними. Высказывание могут принимать только два значения – Истина (обозначается 1) или Ложь (обозначается 0). Высказывания могут быть простыми и составными. Форма мышления
Cлайд 8
Простые высказывания Форма мышления Клубника растёт на деревьях. (ложь) или (0) Два умножить на два равно четырём. (истина) или (1) Все мальчики занимаются футболом. (ложь) или (0) Москва – столица России. (истина) или (1)
Cлайд 9
Простое высказывание состоит из одного высказывания и не содержит логической операции. Составное высказывание содержит высказывания, объединенные логическими операциями. Например, высказывание «Процессор является устройством обработки информации и принтер является устройством печати» является составным высказыванием, состоящим из двух простых, соединённых союзом «и».
Cлайд 10
Сложные высказывания. Форма мышления В саду цветут астры и пионы. Катя любит писать сочинения или решать задачи. Земля движется по круговой или эллиптической орбите. Если на улице дождь, то асфальт мокрый. Голова думает тогда и только тогда, когда язык отдыхает.
Cлайд 11
Предикаты Высказывание состоит из понятий, и его можно сравнить с арифметическим выражением. В математической логике рассматриваются предикаты, т. е. функциональные зависимости от неопределённых понятий (терминов), которые можно сравнить с переменными в уравнении. В предикатах 1 порядка один из терминов является неопределённым понятием: «X – человек». В предикатах 2 порядка два термина неопределённы: «X любит Y». В предикатах 3 порядка неопределённы три термина: «Z – сын X и Y». Преобразуем в высказывания: «Сократ – человек»; «Ксантиппа любит Сократа»; «Софрониск – сын Сократа и Ксантиппы»
Cлайд 12
Умозаключение - это форма мышления, с помощью которой из одного или нескольких высказываний может быть получено новое высказывание. Форма мышления Например, если мы имеем высказывание «Все углы треугольника равны», то мы можем путём умозаключения доказать, что в этом случае справедливо высказывание «Это треугольник равносторонний».
Cлайд 13
В качестве основных логических операций в составных высказываниях используются: НЕ (логическое отрицание, инверсия) ИЛИ (логическое сложение, дизъюнкция) И (логическое умножение, конъюнкция) Операция «ЕСЛИ - ТО» (логическое следование, импликация) Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)
Cлайд 14
Все операции алгебры логики определяются таблицами истинности. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Простые высказывания в алгебре логики обозначаются прописными латинскими буквами: A, B, C, D …
Cлайд 15
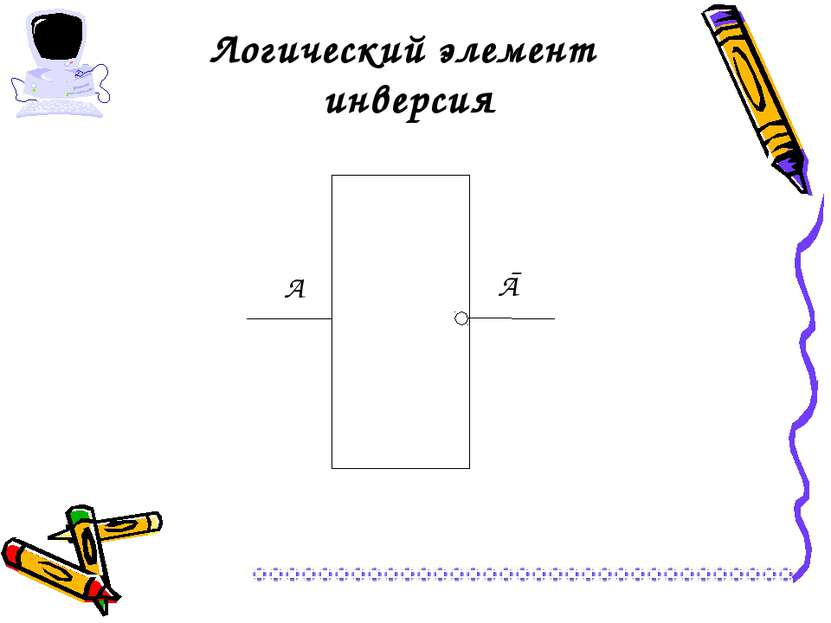
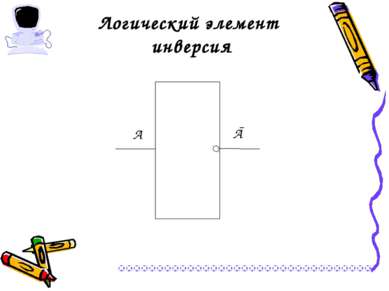
Операция НЕ- логическое отрицание (инверсия) Логическая операция НЕ применяется к одному аргументу, в качестве которого может быть простое и составное высказывание. Обозначение операции НЕ, Ā, not А, ¬ А. А Ā ложь истина истина ложь А Ā 0 1 1 0
Cлайд 16
Логический элемент инверсия
Cлайд 17
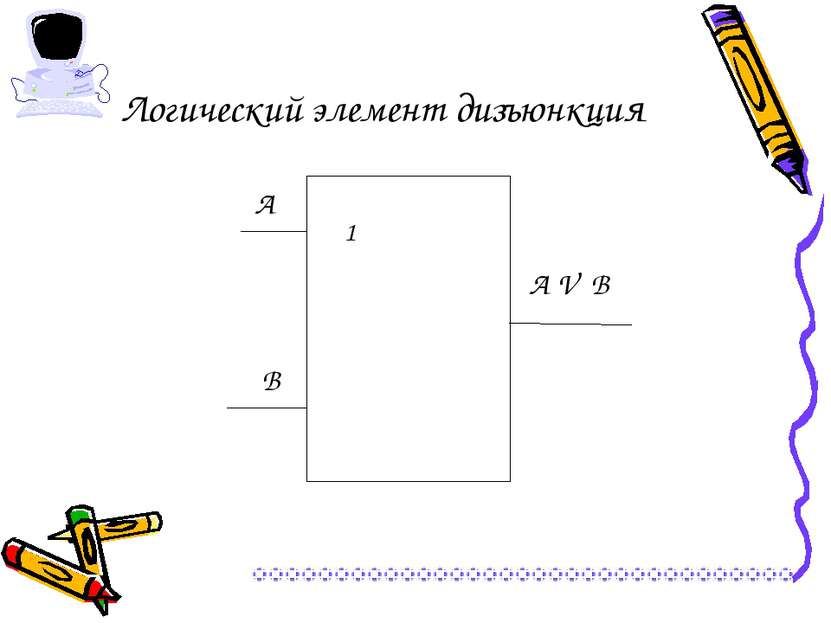
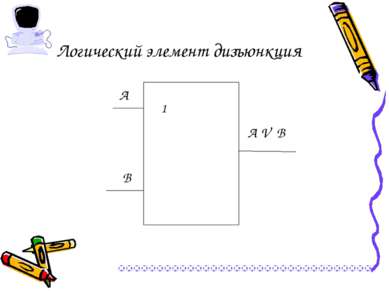
Операция ИЛИ – логическое сложение (дизъюнкция нестрогая, объединение) Выполняет функцию объединения двух высказываний, в качестве которых может быть и простое, и составное высказывание. Обозначения операции: А или В, А or В, А V В. А В АVВ 0 0 0 0 1 1 1 0 1 1 1 1
Cлайд 18
Логический элемент дизъюнкция
Cлайд 19
Операция ИЛИ – логическое сложение (дизъюнкция строгая) Обозначения операции: А xor В, А · В. А В А xor В 0 0 0 0 1 1 1 0 1 1 1 0
Cлайд 20
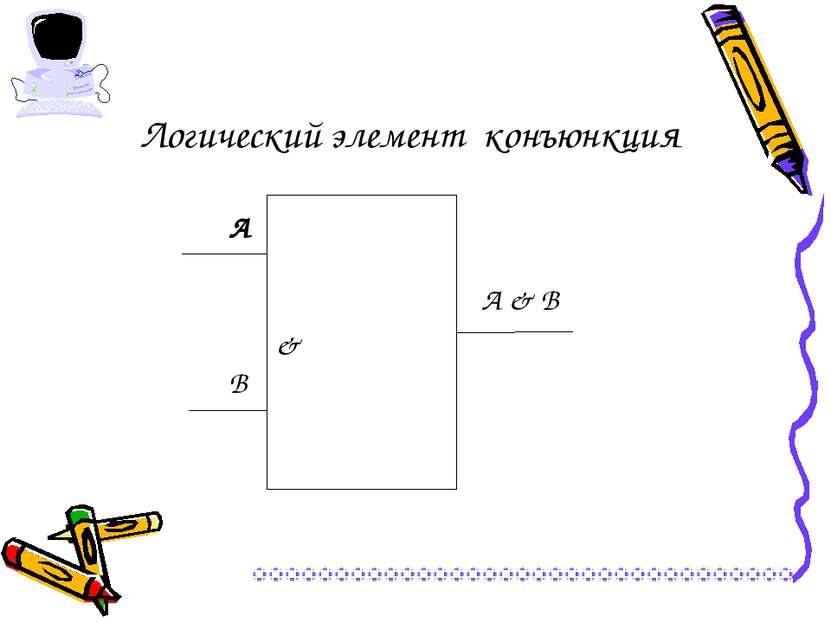
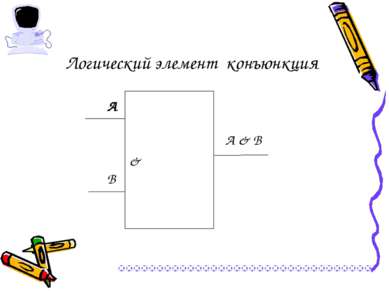
Операция И – логическое умножение (конъюнкция) Выполняет функцию пересечение двух высказываний (аргументов), в качестве которого может быть и простое, и составное высказывание. Обозначения операции: А и В, А & В, А and В, А Λ В. А В А & В 0 0 0 0 1 0 1 0 0 1 1 1
Cлайд 21
Логический элемент конъюнкция
Cлайд 22
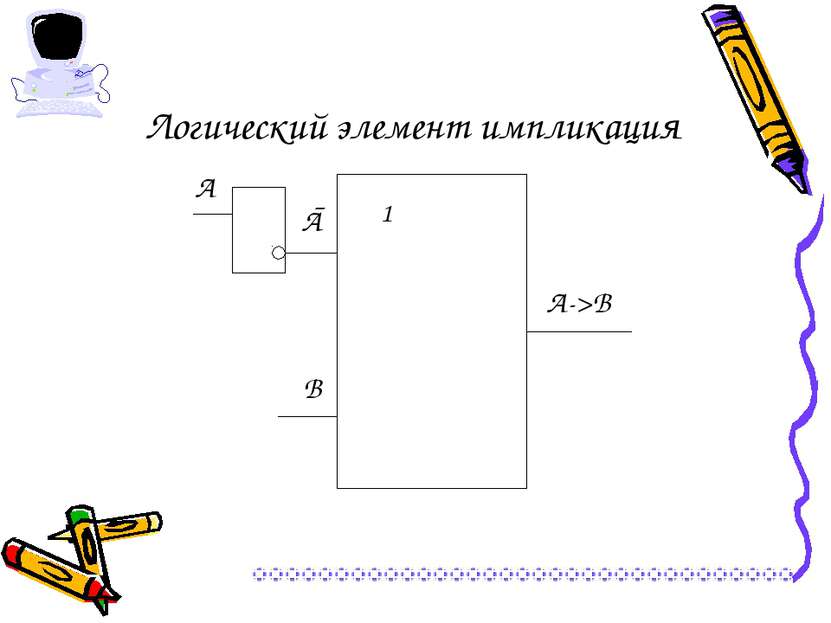
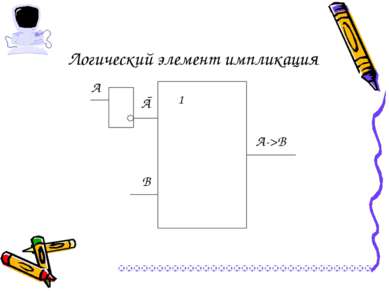
Операция «ЕСЛИ – ТО» - логическое следование (импликация) Связывает два простых высказывания, из которых первое является условием, а второе – следствием из этого условия. Обозначения операции: если А, то В; А влечет В; if A then B; А -> В; А => В А В Если А, то В 0 0 1 0 1 1 1 0 0 1 1 1
Cлайд 23
Логический элемент импликация А
Cлайд 24
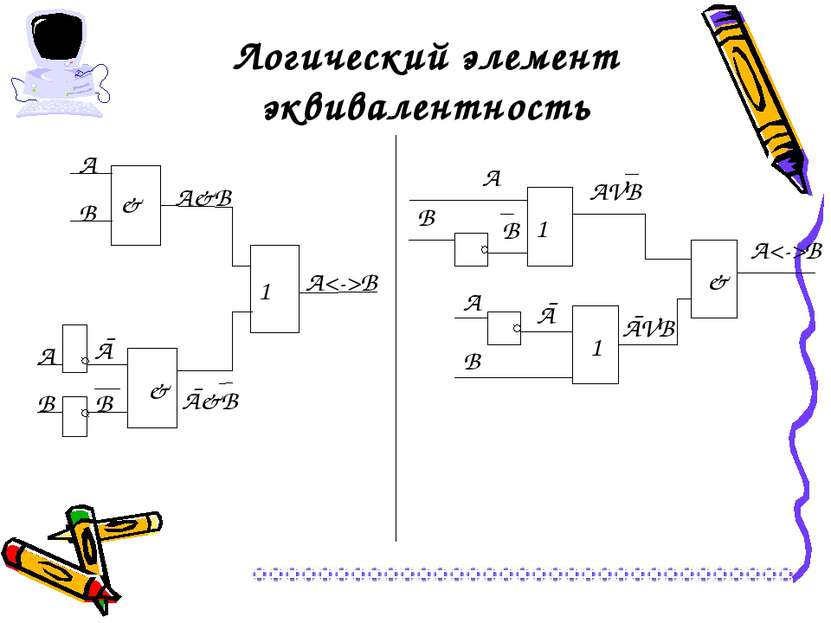
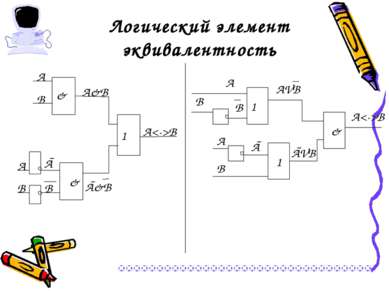
Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность) Обозначения операции: А ~ В, А В, А Ξ В Результат операции эквивалентность истинен тогда и только тогда, когда А и В одновременно истины или ложны. А В А ~ В 0 0 1 0 1 0 1 0 0 1 1 1
Cлайд 25
Логический элемент эквивалентность АВ
Cлайд 26
Каждое составное высказывание можно выразить в виде формулы (логического выражения). Логическое выражение(формула) – содержит логические переменные, обозначающие высказывания, соединённые знаками логических операций.
Cлайд 27
Приоритет логических высказываний действия в скобках инверсия конъюнкция дизъюнкция импликация эквивалентность Пример: U (В ⇒ С) & D ⇔ Ū Порядок вычисления: 1) Ū 2) (В ⇒ С) 3) (В ⇒ С) & D 4) U (В ⇒ С) & D 5) U В ⇒ С & D ⇔ Ū
Cлайд 28
Минипрактикум Даны простые высказывания: A={Процессор – устройство для обработки информации} B={Сканер – устройство вывода информации} C={Монитор – устройство ввода информации} D={Клавиатура – устройство вывода информации} Определите истинность логических выражений: (AVB) (C&D); (A&B) -> (CVD); (AVB) -> (C&D); (A&B) (CVD); (Ā -> B)&(CVD); (C Ā)&B&D; (A&B)VC (A&C)V(A&B); (AVB)VC -> (A&C&D)&(BVD) Проверка
Cлайд 29
Правильные ответы (AVB) (C&D) = 0 (A&B) -> (CVD) = 1 (AVB) -> (C&D) = 0 (A&B) (CVD) = 1 (Ā -> B)&(CVD) = 0 (C Ā)&B&D = 0 (A&B)VC (A&C)V(A&B) = 1 (AVB)VC -> (A&C&D)&(BVD) = 0 A=1 B=0 C=0 D=0 Назад
Cлайд 30
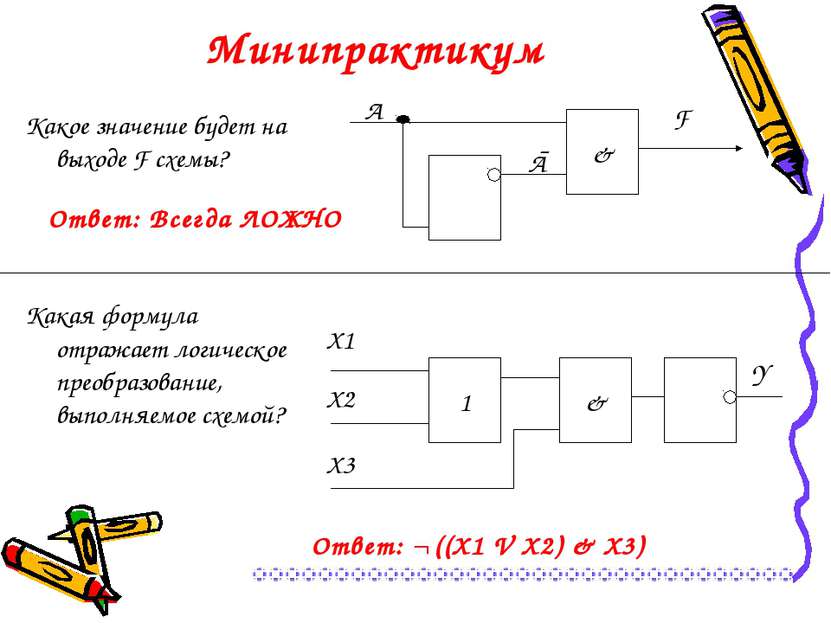
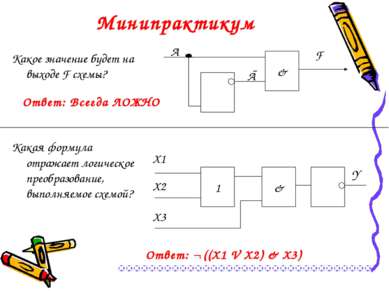Ответ: Всегда ЛОЖНО Минипрактикум Какое значение будет на выходе F схемы? Какая формула отражает логическое преобразование, выполняемое схемой? Ответ: ¬ ((X1 V X2) & X3)
Cлайд 31
Практическая работа ПК Создание в электронных таблицах Microsoft Excel(OpenOffice.org Calc) таблиц истинности логических функций: Конъюнкции Дизъюнкции Инверсии Импликации Эквивалентности
Cлайд 32
Составление таблиц истинности по логической формуле Количество строк - 2ⁿ, где n- это количество логических переменных Количество столбцов - количество логических переменных + количество логических операций. Пример: Ā&В Количество строк = 22 = 4 Количество столбцов = 2 + 2 = 4 А В Ā А&В 0 0 1 0 0 1 1 1 1 0 0 0 1 1 0 0
Cлайд 33
Основные законы булевой алгебры Закон Для дизъюнкции Для конъюнкции 1. Ассоциативность АV(ВVС)=(АVВ)VС= АVВVС А&(В&С)=(А&В)&С= А&В&С 2.Коммутативность АVВ=ВVА А&В=В&А 3.Дистрибутивность (распределение) АV(В&С)=(АVВ)&(АVС) (АVВ)&(ВVС)=(А&С)VВ (АVВ)&С=(А&С)V(B&C) А&ВVС&В=В&(АVС) 4.Идемпотентность АVА=А А&А=А 5.Инволюция Ā=А
Cлайд 34
Основные законы булевой алгебры Закон Для дизъюнкции Для конъюнкции 6.Действие с абсолютно-истинными высказываниями АV1=1 А&1=А 7.Действия с абсолютно-ложными высказываниями АV0=А А&0=0 8.Законы де Моргана АVВ=А&В А&В=АVВ 9.Закон исключенного третьего и закон непротиворечия АVĀ=1 А&Ā=0 10.Поглощения АV(А&В)=А А&(АVВ)=А 11.Поглощение отрицания АV(Ā&В)=АVВ А&(ĀVВ)=А&В
Cлайд 35
Формула склеивания (А В) (А В)=А (А В) (А В)=А
Cлайд 36
Формулы поглощения А (А В)= А А (А В)=А А (Ā В)=А В А (Ā В)=А В
Cлайд 37
Тестовое задание Начать тест
Cлайд 38
Вопросы и задания по теме «Основы логики» Зачёт по теме «Основы логики»
Cлайд 39
Использованные источники Угринович, Н. Д. Информатика и ИКТ. Профильный уровень. Учебник 10-11 классов/Н. Д. Угинович. – М.: БИНОМ. Лаборатория знаний, 2008. Макарова, Н. В. Информатика и ИКТ. Учебник 8-9 класс/Под ред. Проф. Н. В. Макаровой. – СПб.: Питер, 2007. http://ru.wikipedia.org/wiki/%C1%F3%EB%FC,_%C4%E6%EE%F0%E4%E6 http://ru.wikipedia.org/wiki/%C0%F0%E8%F1%F2%EE%F2%E5%EB%FC http://yandex.ru/yandsearch?text=%D0%BB%D0%BE%D0%B3%D0%B8%D0%BA%D0%B0+%D0%B8+%D0%BA%D0%BE%D0%BC%D0%BF%D1%8C%D1%8E%D1%82%D0%B5%D1%80+%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8&lr=64
