X
Код презентации скопируйте его
Измерение информации: алфавитный подход
Скачать эту презентацию
Презентация на тему Измерение информации: алфавитный подход
Скачать эту презентациюCлайд 1
Измерение информации: алфавитный подход Информация и информационные процессы *
Cлайд 2
Как измерить информацию? Вопрос: «Как измерить информацию?» очень непростой. Ответ на него зависит от того, что понимать под информацией. Но поскольку определять информацию можно по-разному, то и способы измерения тоже могут быть разными. *
Cлайд 3
Алфавитный подход к измерению информации Познакомимся с способом измерения информации, который не связывает количество информации с содержанием сообщения, и называется он алфавитным подходом. При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы. *
Cлайд 4
Алфавит и его мощность Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами. Полное количество символов алфавита принято называть мощностью алфавита. Будем обозначать эту величину буквой N. Например, мощность алфавита из заглавных русских букв без буквы ё равна 32. АБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЪЭЮЯ *
Cлайд 5
Сколько информации несет один символ в русском языке Представьте себе, что текст к вам поступает последовательно, по одному знаку, словно бумажная ленточка, выползающая из телеграфного аппарата. Предположим, что каждый появляющийся на ленте символ с одинаковой вероятностью может быть любым символом алфавита. В каждой очередной позиции текста может появиться любой из N символов. Тогда, согласно известной нам формуле 2I = N , каждый такой символ несет I бит информации, которое можно определить из решения уравнения: 2I = 32. Получаем: I = 5 бит. *
Cлайд 6
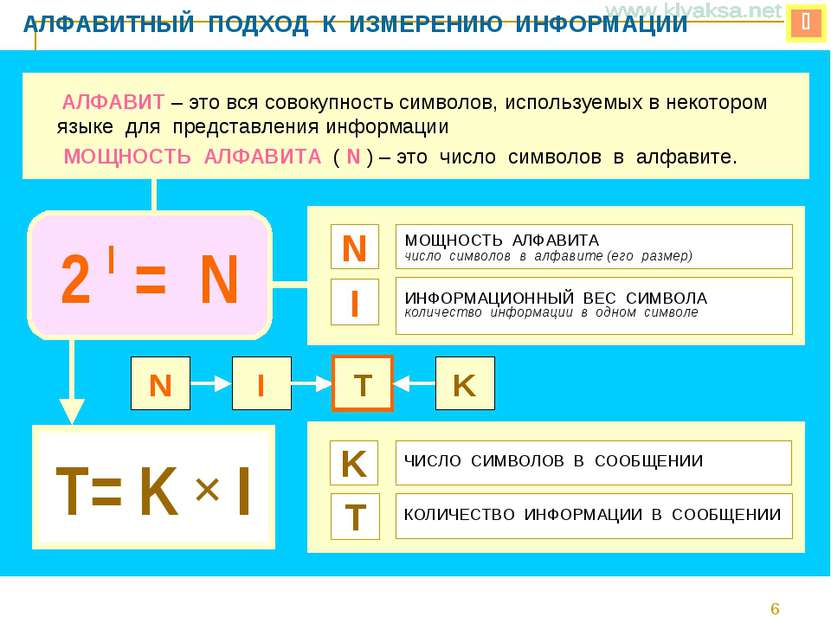
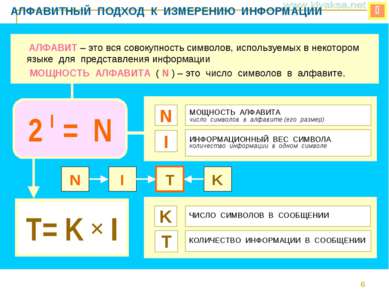АЛФАВИТНЫЙ ПОДХОД К ИЗМЕРЕНИЮ ИНФОРМАЦИИ МОЩНОСТЬ АЛФАВИТА число символов в алфавите (его размер) N ИНФОРМАЦИОННЫЙ ВЕС СИМВОЛА количество информации в одном символе T= K I I АЛФАВИТ – это вся совокупность символов, используемых в некотором языке для представления информации МОЩНОСТЬ АЛФАВИТА ( N ) – это число символов в алфавите. 2 I = N ЧИСЛО СИМВОЛОВ В СООБЩЕНИИ K КОЛИЧЕСТВО ИНФОРМАЦИИ В СООБЩЕНИИ T N I T K *
Cлайд 7
Задание Племя Мумбу-Юмбу использует алфавит из букв: αβγδεζηθλμξσφψ, точки и для разделения слов используется пробел. Сколько информации несет фраза из 20 символов на языке племени? Ответ: 16 = 24, I = 4 бита. Т = 4 * 20 = 80 бит = 10 байт. *
Cлайд 8
Достаточный алфавит Удобнее всего измерять информацию, когда размер алфавита N равен целой степени двойки. Например, если N=16, то каждый символ несет 4 бита информации потому, что 24 = 16. А если N =32, то один символ «весит» 5 бит. Ограничения на максимальный размер алфавита теоретически не существует. Однако есть алфавит, который можно назвать достаточным. Это алфавит мощностью 256 символов. Поскольку 256 = 28, то один символ этого алфавита «весит» 8 бит. Причем 8 бит информации — это настолько характерная величина, что ей даже присвоили свое название — байт. 1 байт = 8 бит *
Cлайд 9
Количество информации в тексте Посчитаем количество информации на одной странице книги. Пусть страница содержит 50 строк. В каждой строке — 60 символов. Значит, на странице умещается 50x60=3000 знаков. Тогда объем информации будет равен: 8 х 3000 = 24 000 бит = 3000 байт = 2,9 Кбайт. При алфавитном подходе к измерению информации количество информации зависит не от содержания, а от размера текста и мощности алфавита. *
Cлайд 10
Задание: Вычислите какова мощность алфавита, с помощью которого записано сообщение, содержащее 2048 символов, если его объем составляет 1.25 Кбайта. *
Cлайд 11
Решение Дано: К=2048, Т = 1,25 Кбайт. Найти: N. Решение. Т=1,25 Кбайт = 1280 байт = 10240 бит. T=K * I, I = T / K = 10240 / 2048 = 5 бит. N = 2 I = 2 5 = 32 символа. *
