X
Код презентации скопируйте его
Системы счисления 10 класс
Скачать эту презентацию
Презентация на тему Системы счисления 10 класс
Скачать эту презентациюCлайд 1
Системы счисления
Cлайд 2
СИСТЕМА СЧИСЛЕНИЯ - это способ изображения чисел и соответствующие ему правила действия над числами. I, II, III, IV, V, VI, VII,…. 1, 2, 3, 4, 5, 6, 7, 8, 9,0
Cлайд 3
Основание системы, к которой относится число, обозначается подстрочным индексом к этому числу. 10110123, 3671810, 3В8F1616. основание система алфавит n = 2 двоичная 0, 1 n = 3 троичная 0, 1, 2 n = 8 восьмеричная 0,1, 2, 3, 4, 5, 6, 7 n = 16 шестнадцатеричная 0, 1 ..9, A, B, C, D, E, F
Cлайд 4
Чтобы перевести из десятичной системы счисления в другую надо: данное десятичное число делится на основание системы с остатком; полученный остаток - это младший разряд искомого числа, а полученное частное снова делится на основание, остаток равен второй справа цифре и так далее; так продолжается до тех пор, пока частное не станет меньше делителя (основания системы). Это частное - старшая цифра искомого числа.
Cлайд 5
Таблица перевода из двоичной записи в восьмеричную и наоброт Например, 10101101011112 = 1 010 110 101 1112 = 126578 438 = 100 0112 Восьмиричная запись Двоичная запись 0 1 2 3 4 5 6 7 000 001 010 011 100 101 110 111
Cлайд 6
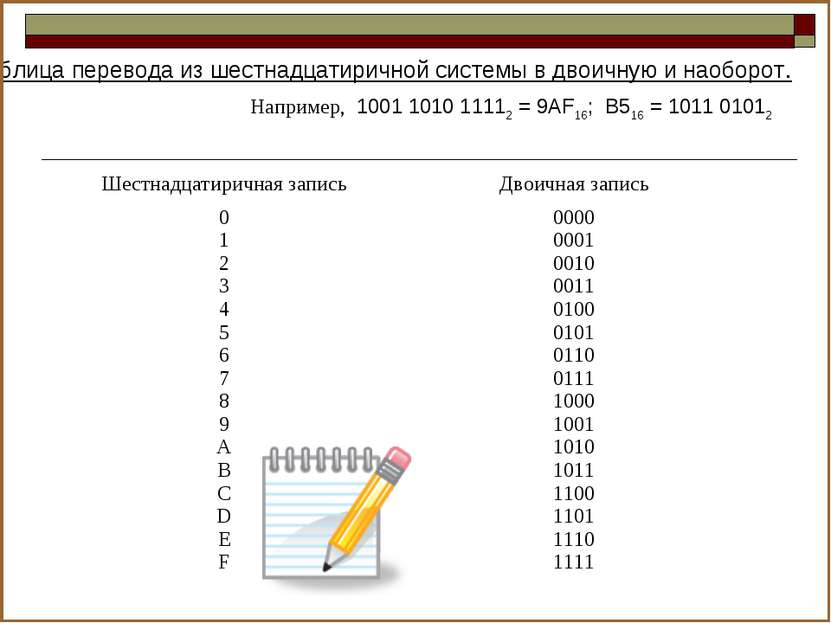
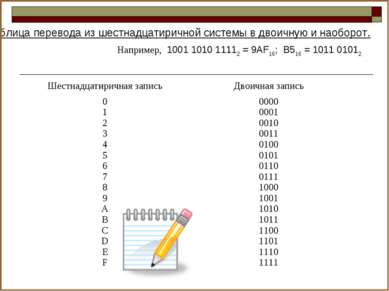Таблица перевода из шестнадцатиричной системы в двоичную и наоборот. Например, 1001 1010 11112 = 9AF16; B516 = 1011 01012 Шестнадцатиричная запись Двоичная запись 0 1 2 3 4 5 6 7 8 9 A B C D E F 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
Cлайд 7
Алгоритм перевода из одной системы в другую без таблицы. Перевести число в десятичную систему счисления. Из десятичной перевести в нужную систему счисления. Например, перевести 1011012 в пятеричную запись. 1011012 = 1 25 + 0*24 + 1*23 + 1*22 + 0*21+1*20 = 32 + 8 + 4 + 1 = 4510 45 : 5 = 9 (ост. 0) 9 : 5 = 1 (ост 4) 4510 = 1405, то есть 1011012 = 1405 Перевести число 23С16 в восьмеричное. 23С16 = 2*162 + 3*161 + 12*160 = 2*256 + 48 + 12 = 512 + 60 = 57210 572 : 8 = 71 (ост. 4) 71 : 8 = 8 (ост. 7) 8 : 8 = 1(ост.0) 23С10 = 57210 = 10748
Cлайд 8
Практическая работа Выполнить перевод чисел из десятичной системы счисления в двоичную: 1510; 2610; 10110 Выполнить перевод из двоичной системы счисления в десятичную: 110112; 110012; 11102
Cлайд 9
Примеры: 37 : 2 = 18(ост1 - младший разряд) 18 : 2 = 9 (ост 0) 9 : 2 = 4(ост 1) 4 : 2 = 2 (ост 0); 2: 2 = 1 (0ст 0) . 3710 = 1001012 15 : 2 = 7(ост 1) 7: 2 = 3(ост 1) 3 : 2 = 1 (ост 1) 1510 = 11112
Cлайд 10
Двоичная арифметика 1. Сложение: 0 + 0 = 0; 1 + 0 = 1; 1 + 1 = 10. Пример: 1011011101 + 111010110 10010110011 Умножение: 0 * 0 = 0; 1 * 0 = 0; 1 * 1 = 1. Пример: 1101101 * 101 1101101 1101101 1000100001
Cлайд 11
Двоичная арифметика Вычитание: 0 - 0 = 0; 1 - 0 = 1; 1 -1 = 0. Пример: 101 - 11 1 0 4. Деление: 10111010111 : 1101 = 11100 Задания для самостоятельной работы: 1. Сложить двоичные числа 1111112+10012; 11001112+11012; 1001112+1110002 2. Вычесть: 1100112-10012; 1111112-10012; 11001112-11012 3. Умножить: 11012*112; 10112*1012; 1102*102
Cлайд 12
Двоичная кодировка. В современной вычислительной технике информация чаще всего кодируется с помощью последовательностей сигналов всего двух видов: намагничено или не намагничено, включено, не выключено, высокое напряжение или низкое и так далее. Принято одно состояние обозначать цифрой 1, а другое – 0, а цифры 0 и 1 называть битами. При двоичном кодировании каждому символу сопостовляется его код – последовательность из фиксированного количества нулей и единиц. В большинстве современных ЭВМ каждому символу соответствует последовательность из 8 нулей и 1, называемая БАЙТОМ. Всего существует 256 разных последовательностей из 8 нулей и единиц – это позволяет закодировать 256 разных символов, например, буквы, цифры, знаки препинания и так далее. Соответствие байтов и символов задается с помощью таблицы, в которой для каждого кода указывается соответствующий символ.
Cлайд 13
Пример Коду 00100000 в этой таблице соответствует пробел. Коды русских букв отличаются от кодов латинских букв. Например, большая русская буква «М» имеет код 11101101, бука «И» – 11101001, буква «Р» – 11110010. Слово «МИР» шифруется так: 11101101111010011110010 и несет 24 бита информации или 3 байта. 111011011110100111101101 – РИМ – 24 бита или 3 байта.
Cлайд 14
Как подсчитать сколько информации несет то или иное издание? Каждый символ несет 1 байт или 8 битов. На страницу учебника помещается примерно 50 строк, в каждой строке – примерно – 60 знаков (60 байт). Значит, полностью заполненная страница имеет информационный объем около 3000 байт. Так 1 Кбайт = 210 байт = 1024 байта 1000 байта, то объем одной страницы примерно равен 3 Кбайта В учебнике 250 страниц, то 3 * 250 = 750 Кбайт. В одном томе Большой Советской Энциклопедии примерно 120 Мбайт. В одном номере четырехстраничной газеты – 150 Кбайт
Cлайд 15
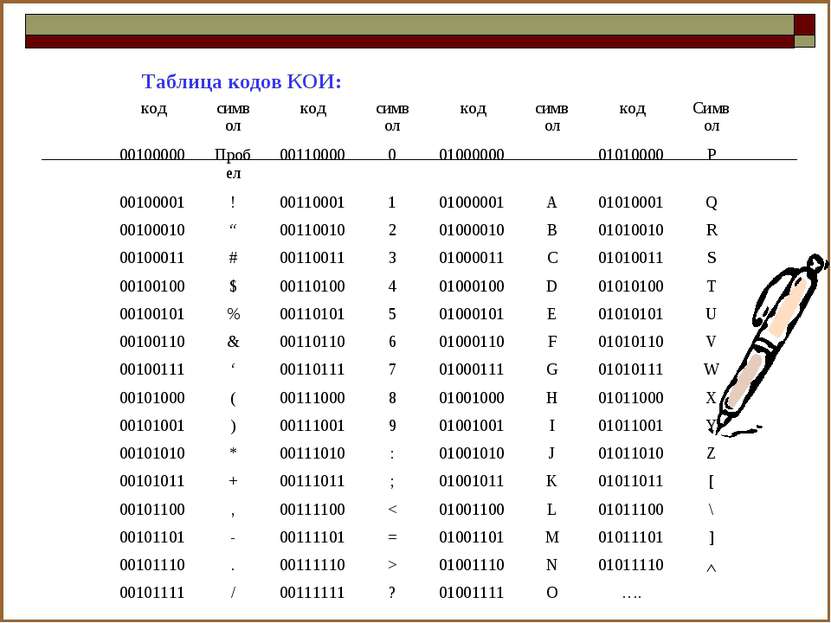
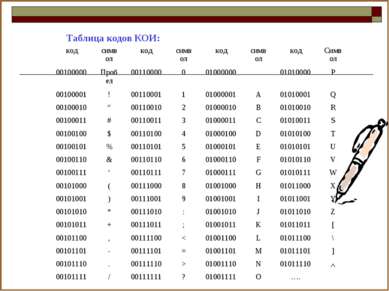Таблица кодов КОИ: код символ код символ код символ код Символ 00100000 Пробел 00110000 0 01000000 01010000 P 00100001 ! 00110001 1 01000001 A 01010001 Q 00100010 “ 00110010 2 01000010 B 01010010 R 00100011 # 00110011 3 01000011 С 01010011 S 00100100 $ 00110100 4 01000100 D 01010100 T 00100101 % 00110101 5 01000101 E 01010101 U 00100110 & 00110110 6 01000110 F 01010110 V 00100111 ‘ 00110111 7 01000111 G 01010111 W 00101000 ( 00111000 8 01001000 H 01011000 X 00101001 ) 00111001 9 01001001 I 01011001 Y 00101010 * 00111010 : 01001010 J 01011010 Z 00101011 + 00111011 ; 01001011 K 01011011 [ 00101100 , 00111100 < 01001100 L 01011100 \ 00101101 - 00111101 = 01001101 M 01011101 ] 00101110 . 00111110 > 01001110 N 01011110 00101111 / 00111111 ? 01001111 O ….
Cлайд 16
Единицы измерения информации. 1 Кбит = 210 = 1024 бит ( 1 тыс. бит) 1 Мбит = 220 = 1048576 бит ( 1 млн. бит) 1 Гбит = 230 109 бит (миллиард бит) 1 Кбайт = 210 = 1024 байт ( 1 тыс. байт) 1 Мбайт = 220 = 1048576 байт ( 1 млн. байт) 1 Гбайт = 230 ( 1 млрд. байт)
