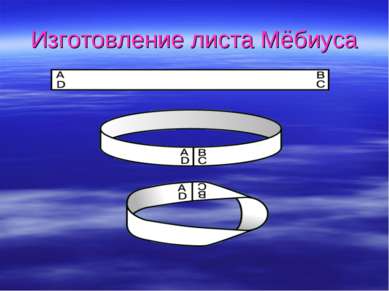
X
Код презентации скопируйте его
Лист Мёбиуса
Скачать эту презентацию
Презентация на тему Лист Мёбиуса
Скачать эту презентациюCлайд 1
Лист Мёбиуса Презентация по математике на тему: Выполнила ученица 8 класса Холязинской основной школы Вантеева Екатерина
Cлайд 2
Задачи проекта: самостоятельно найти литературу о листе Мёбиуса; экспериментальным путём выяснить свойства листа Мёбиуса; показать необычность этой геометрической поверхности; убедить в том, что лента Мёбиуса нашла применение во многих привычных для нас сферах жизни; доказать актуальность выбранной мною темы.
Cлайд 3
Изготовление листа Мёбиуса
Cлайд 4
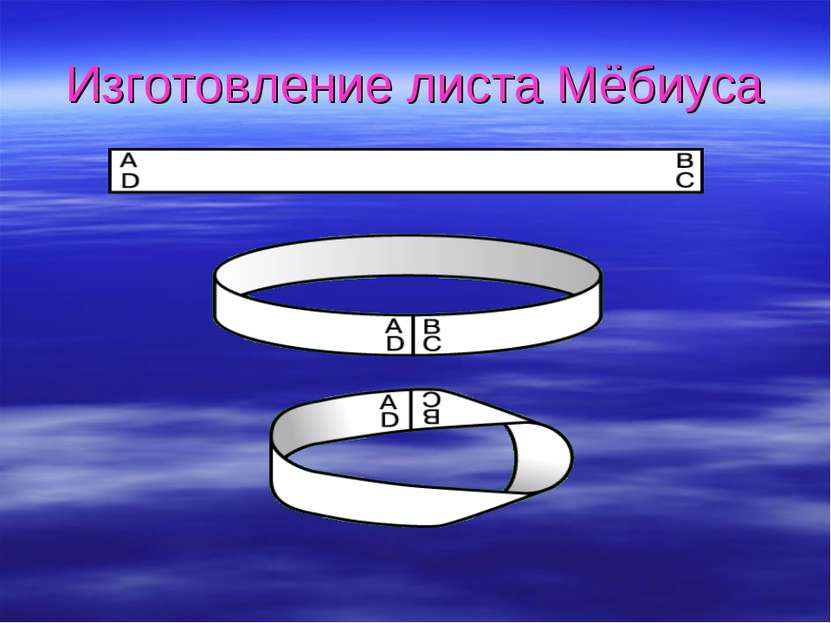
Лист Мёбиуса – один из объектов области математики под названием «топология», по-другому – «геометрия положений». Удивительные свойства листа Мёбиуса – он имеет один край, одну сторону, – не связаны с его положением в пространстве, с понятиями расстояния, угла и, тем не менее, имеют вполне геометрический характер. Изучением таких свойств занимается топология.
Cлайд 5
Таинственный и знаменитый лист Мёбиуса открыл в 1858 г. немецкий геометр Август Мёбиус(1790-1868), ученик «короля математики» Гаусса. Директор Лейпцигской астрономической обсерва-тории, А.Мёбиус был разносторонним учёным. В те времена занятия математи-кой не встречали поддержки, а должность в обсерватории давала достаточно денег, чтобы не думать о них и оставляла время для размышлений. И Мёбиус стал одним из крупнейших геометров своего времени. Мёбиус Август Фердинанд В возрасте 68 лет ему удалось сделать открытие порази-тельной красоты. Он открыл односторонние поверхности, одна из которых – лист Мёбиуса. Мёбиус является одним из осно-вателей современной топологии.
Cлайд 6
Эксперименты для всех
Cлайд 7
вопрос гипотеза эксперимент Число перекручиваний 0. Что будет, если разрезать кольцо? Получим 2 кольца, которые уже в 2 раза Получили 2 кольца, которые уже в 2 раза Число перекручиваний 1. Что будет, если ЛМ разрезать вдоль посередине Получим 2 кольца Кольцо, перекрученное на 2 полуоборота, оно уже в 2 раза исходного На разных сторонах ЛМ сидят муха и паук. Может ли паук подкрасться к мухе, не переходя через край ленты? Да, сможет По неперекрученному кольцу нет, а по перекрученному - да
Cлайд 8
Искусство и технология Международный символ переработки представляет собой Лист Мёбиуса. Чудесные свойства ленты тут же породили множество научных трудов, изобретений, а также многочисленных фантастических рассказов.
Cлайд 9
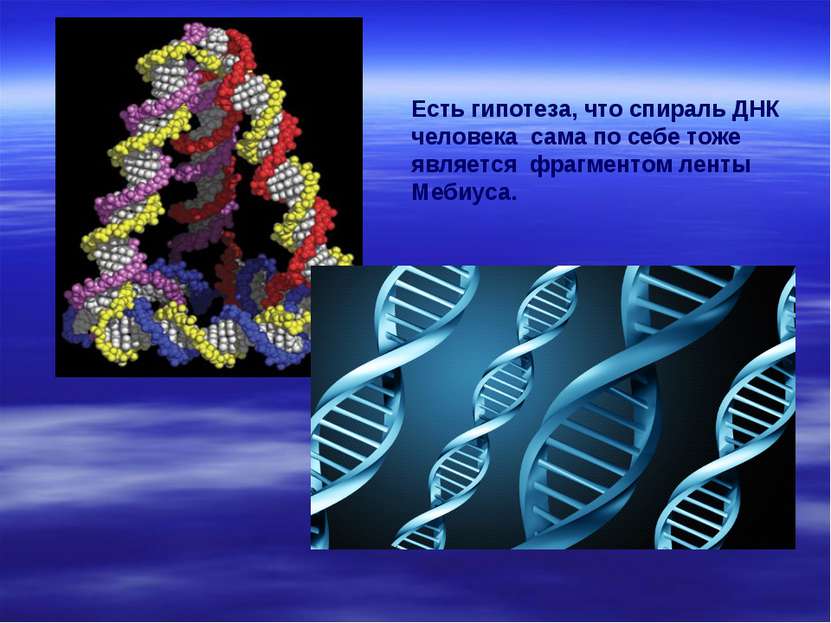
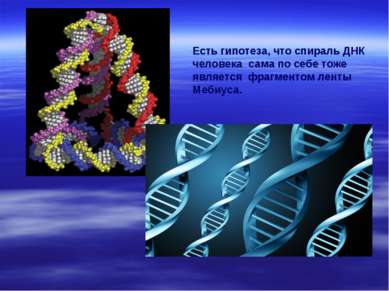Есть гипотеза, что спираль ДНК человека сама по себе тоже является фрагментом ленты Мебиуса.
Cлайд 10
Невероятный проект новой библиотеки в Астане, Казахстан.
Cлайд 11
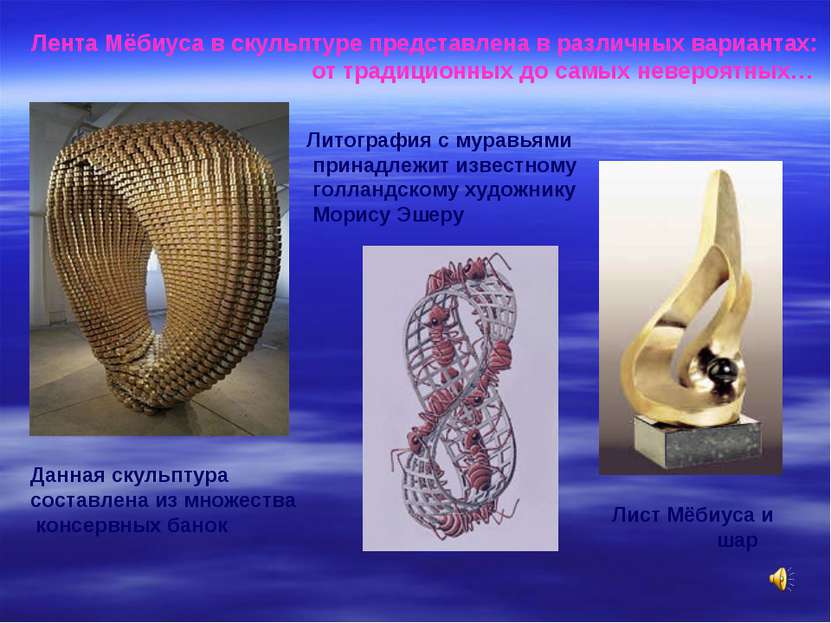
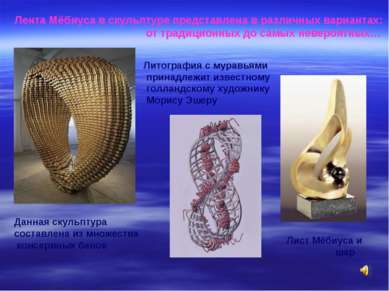Лента Мёбиуса в скульптуре представлена в различных вариантах: от традиционных до самых невероятных… Данная скульптура составлена из множества консервных банок Лист Мёбиуса и шар Литография с муравьями принадлежит известному голландскому художнику Морису Эшеру
Cлайд 12
Монумент у здания Президиума Национальной академии наук В Минске Памятник ленте Мёбиуса в Москве
Cлайд 13
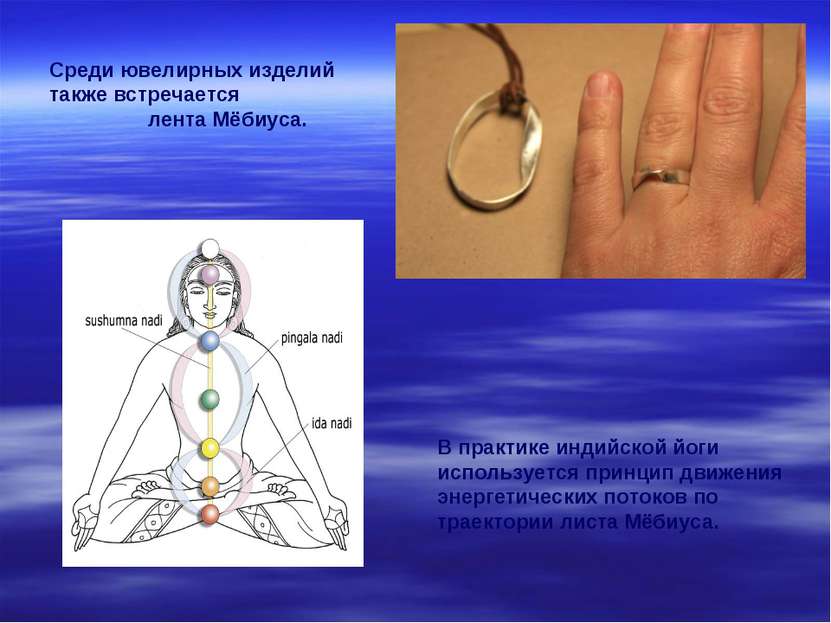
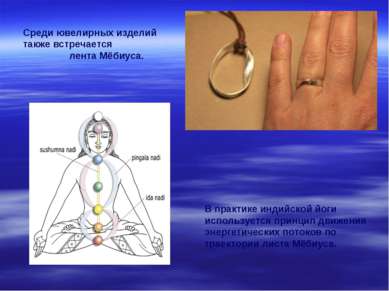В практике индийской йоги используется принцип движения энергетических потоков по траектории листа Мёбиуса. Среди ювелирных изделий также встречается лента Мёбиуса.
Cлайд 14
Лист Мебиуса – символ математики, Что служит высшей мудрости венцом… Он полон неосознанной романтики: В нем бесконечность свернута кольцом. В нем – простота, и вместе с нею – сложность, Что недоступна даже мудрецам: Здесь на глазах преобразилась плоскость В поверхность без начала и конца. Здесь нет пределов, нет ограничений, Стремись вперед и открывай миры, Почувствуй силу новых ощущений, Прими познанья высшего дары.
Cлайд 15
Выводы о проделанной работе: прочитав определённую литературу, я познакомилась с геометрической поверхностью лентой Мёбиуса; анализируя собранный материал, я увидела необычность этой ленты; экспериментальным путём я показала, что лист Мёбиуса является односторонней поверхностью, что необычно для трёхмерной фигуры; я провела восемь опытов с листом и доказала, что он изменяет свои свойства при разрезании; увидела, что усложнение эксперимента не приводит к более эффектным результатам; пыталась убедить, что лента Мёбиуса нашла применение во многих привычных для нас сферах жизни; считаю правильным, что лист Мёбиуса считают символом современной математики, так как именно он дал толчок новым математическим исследованиям.
Cлайд 16
