X
Код презентации скопируйте его
Теорема Фалеса 8 класс
Скачать эту презентациюПрезентация на тему Теорема Фалеса 8 класс
Скачать эту презентациюCлайд 2
 Фалес Милетский Древнегреческий философ, родоначальник античной и вообще европейской философии и науки, основатель милетской школы. Сочинения Фалеса не сохранились, однако Аристотель называет его первым ионийским философом. Важнейшей заслугой Фалеса в области математики считается перенесение им из Египта в Грецию первых начал теоретической элементарной геометрии: • Вертикальные углы равны. • Углы при основании равнобедренного треугольника равны. • Треугольник определяется стороной и прилежащими к ней двумя углами. • Диаметр делит круг на две равные части. Фалесу приписывается решение двух геометрических задач практического характера: определения расстояния корабля на море от Милетской гавани и определения высоты пирамиды по длине её тени.
Фалес Милетский Древнегреческий философ, родоначальник античной и вообще европейской философии и науки, основатель милетской школы. Сочинения Фалеса не сохранились, однако Аристотель называет его первым ионийским философом. Важнейшей заслугой Фалеса в области математики считается перенесение им из Египта в Грецию первых начал теоретической элементарной геометрии: • Вертикальные углы равны. • Углы при основании равнобедренного треугольника равны. • Треугольник определяется стороной и прилежащими к ней двумя углами. • Диаметр делит круг на две равные части. Фалесу приписывается решение двух геометрических задач практического характера: определения расстояния корабля на море от Милетской гавани и определения высоты пирамиды по длине её тени.
Cлайд 3
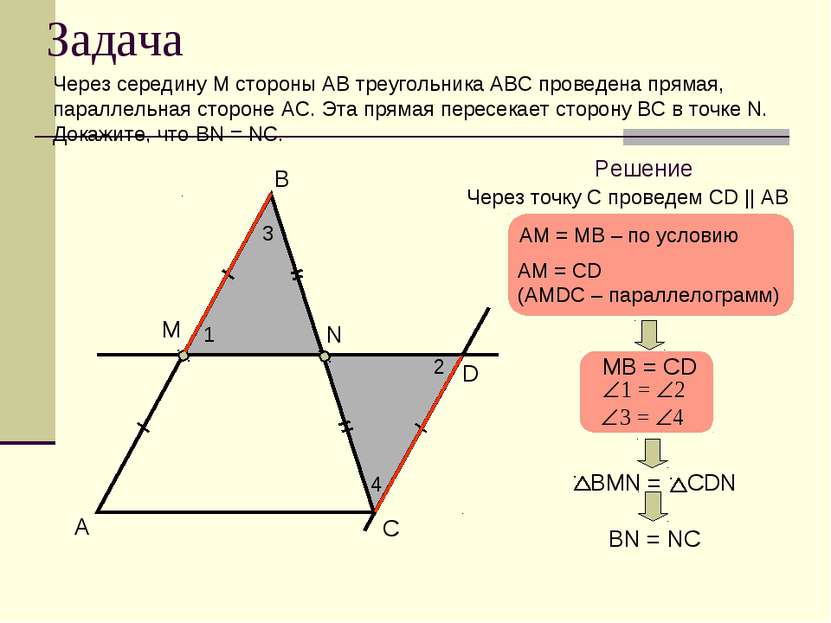
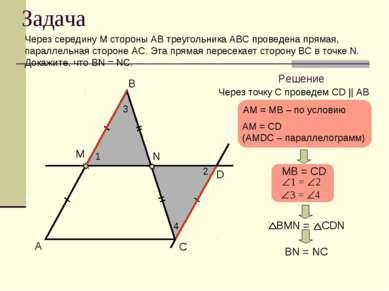 Задача Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне AС. Эта прямая пересекает сторону BС в точке N. Докажите, что BN = NC. A B C M D N Решение Через точку С проведем СD || AB AM = MB – по условию AM = СD (AMDC – параллелограмм) MВ = CD 1 2 3 4 BN = NC
Задача Через середину М стороны АВ треугольника АВС проведена прямая, параллельная стороне AС. Эта прямая пересекает сторону BС в точке N. Докажите, что BN = NC. A B C M D N Решение Через точку С проведем СD || AB AM = MB – по условию AM = СD (AMDC – параллелограмм) MВ = CD 1 2 3 4 BN = NC
Cлайд 4
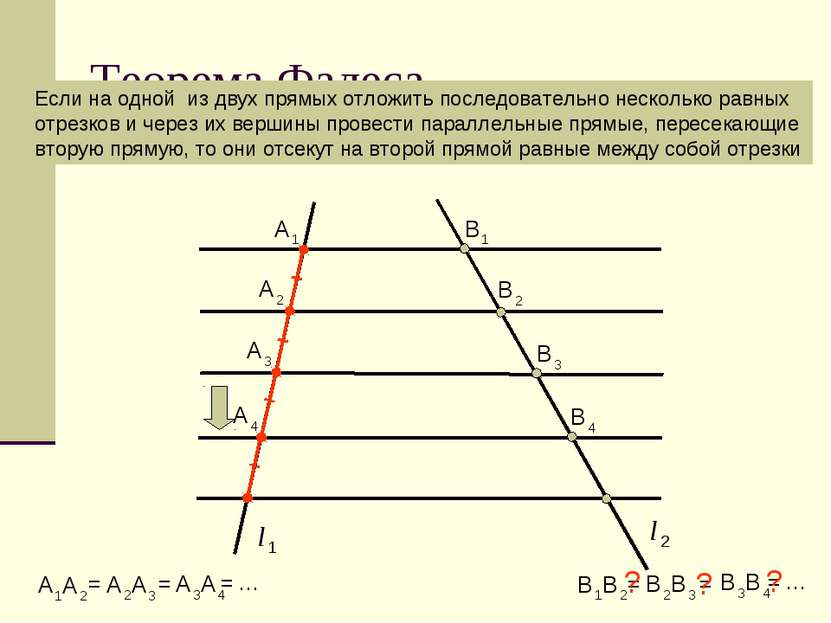
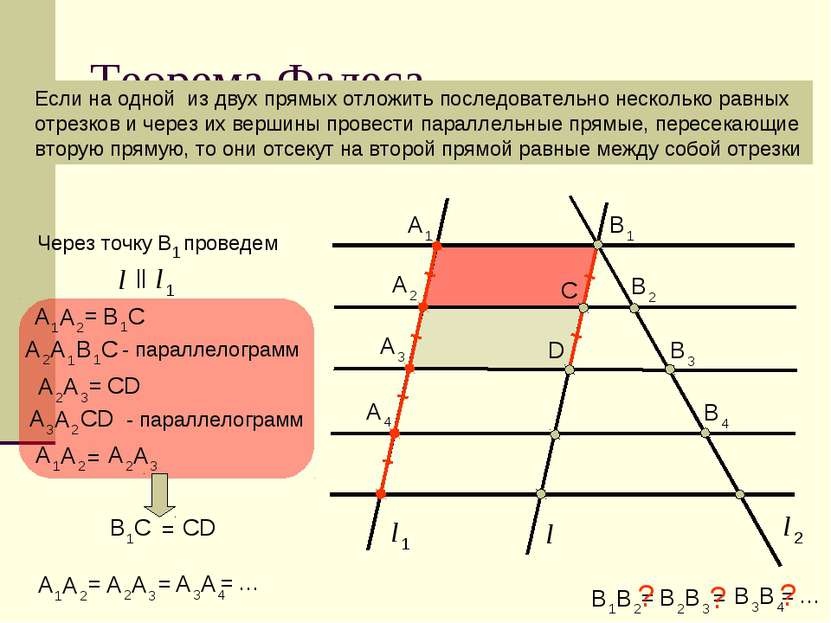
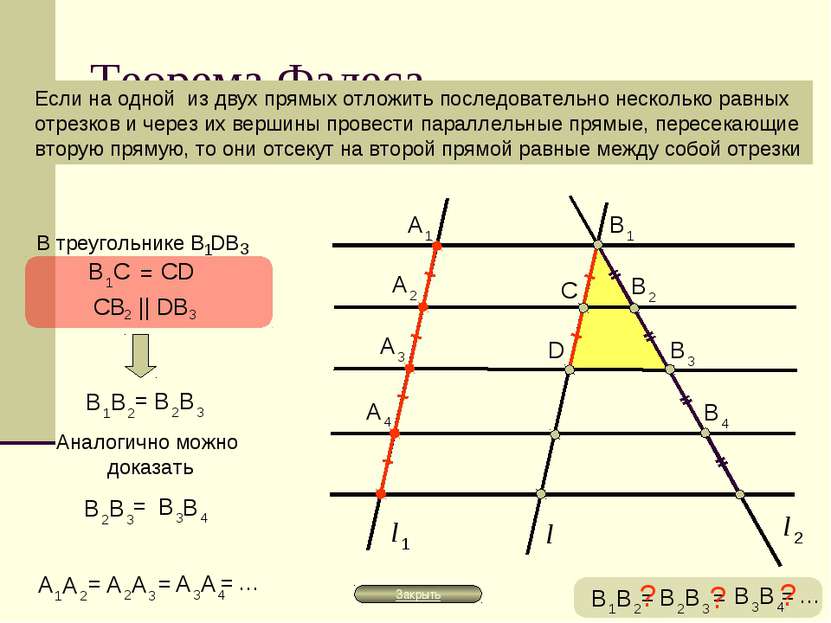
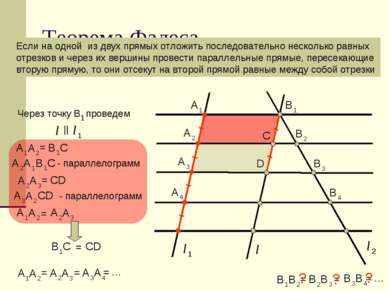
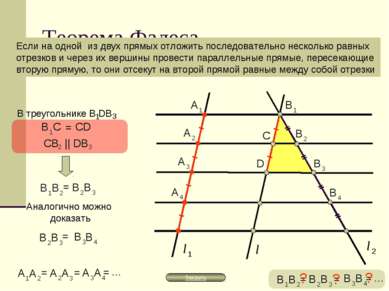
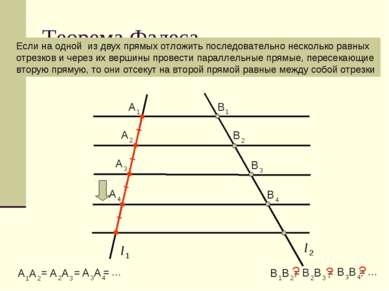 Теорема Фалеса Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их вершины провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки = = = … = = = … ? ? ?
Теорема Фалеса Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их вершины провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки = = = … = = = … ? ? ?