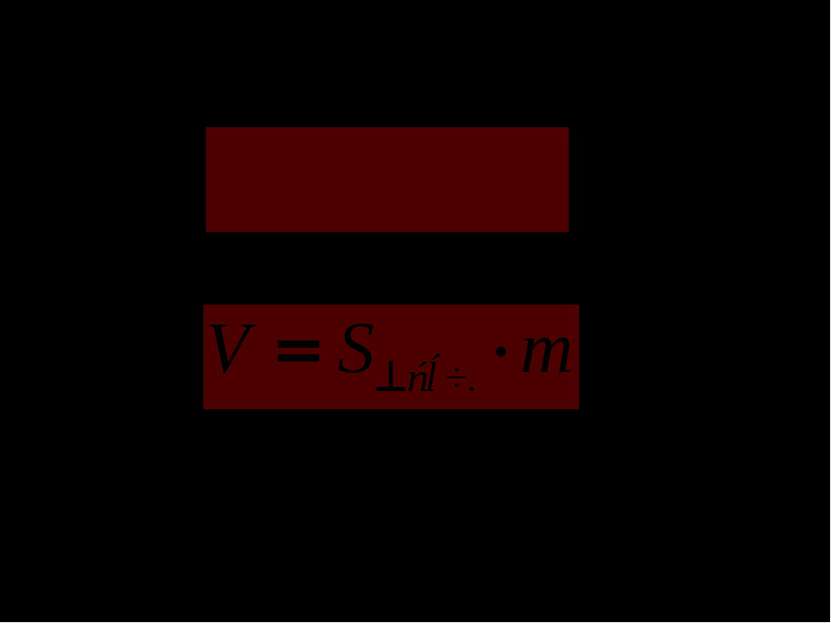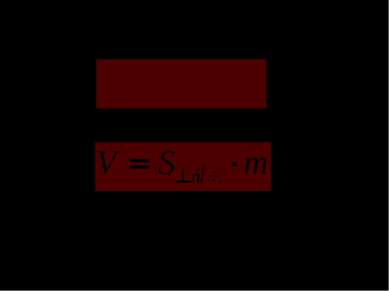X
Код презентации скопируйте его
Понятие объема. Объем призмы
Скачать эту презентацию
Презентация на тему Понятие объема. Объем призмы
Скачать эту презентациюCлайд 1
Понятие объема. Объем призмы. Геометрия, 11 класс Воробьев Леонид Альбертович, г.Минск
Cлайд 2
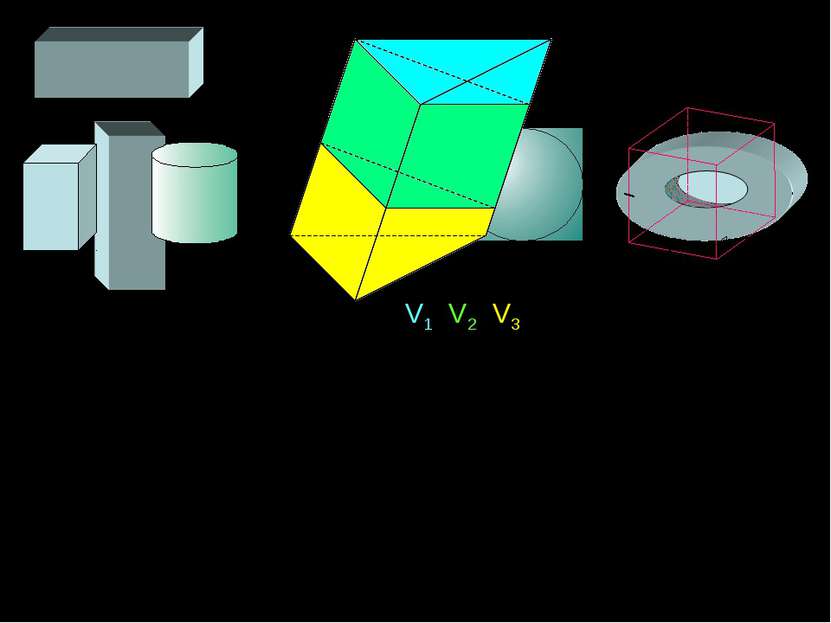
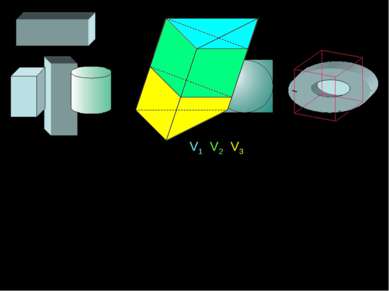Любое геометрическое тело в пространстве характеризуется величиной, называемой ОБЪЕМОМ. Так что же такое – объем пространственной фигуры? Под объемом пространственной фигуры понимается положительная величина, обладающая следующими свойствами: равные фигуры имеют равные объемы; объем фигуры равен сумме объемов ее частей; объем куба с ребром единичной длины равен одной кубической единице. V1=V2 V=V1+V2+V3 V=1 куб.ед.
Cлайд 3
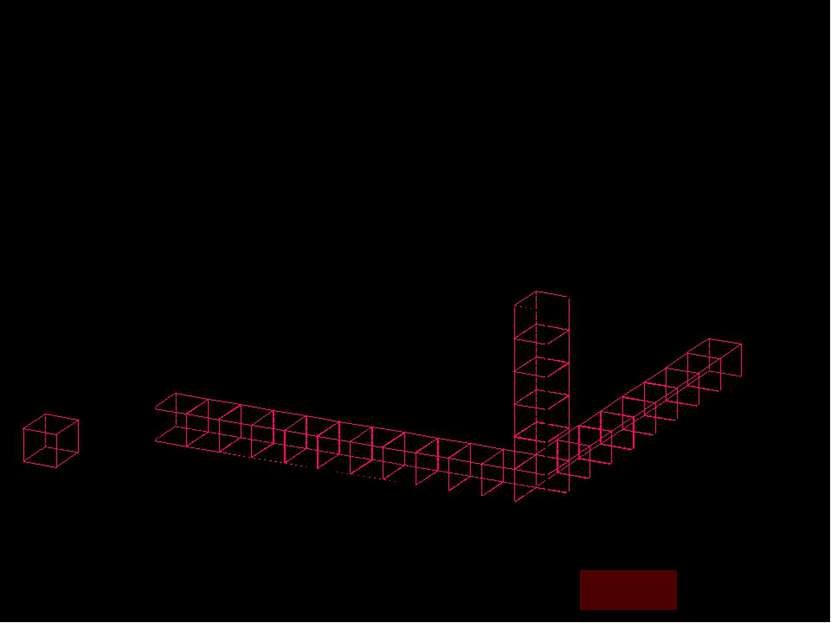
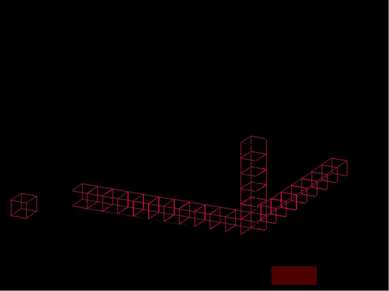a b c=H a b c Самым естественным образом определяется объем прямоугольного параллелепипеда, как геометрического тела составленного из определенного количества единичных кубов. А значит, его объем определяется как сумма объемов этих единичных кубов.
Cлайд 4
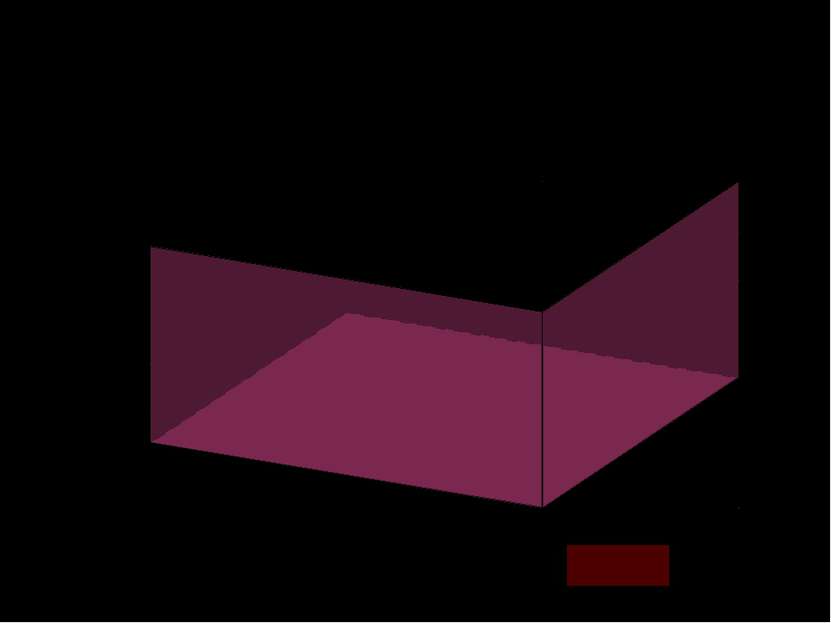
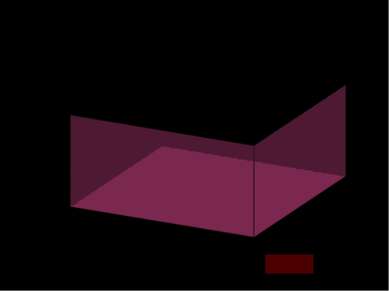a b c=H Эту же формулу объема прямоугольного параллелепипеда можно получить пользуясь понятием бесконечной интегральной суммы. Объем прямоугольного параллелепипеда можно понимать как бесконечную сумму площадей основания, взятых вдоль его высоты. x 0 x x [ 0; H ]
Cлайд 5
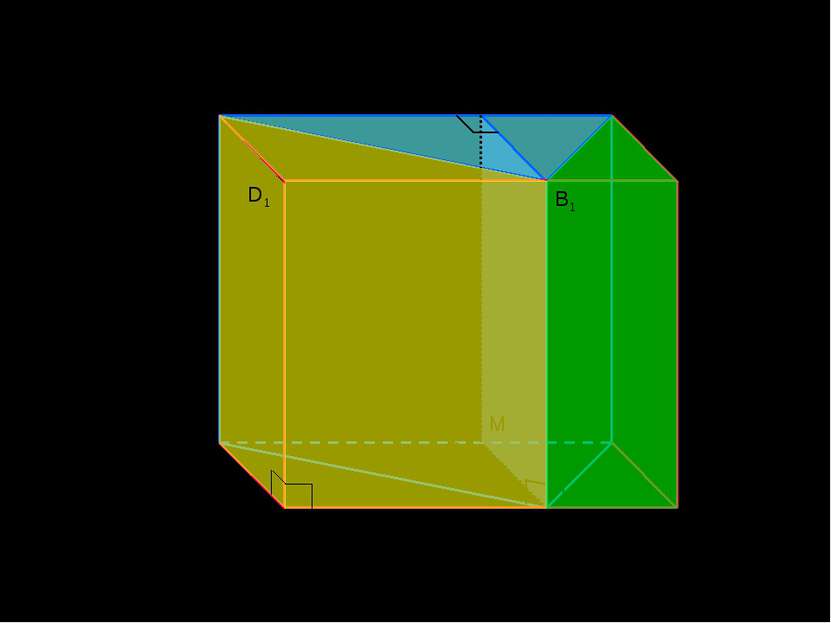
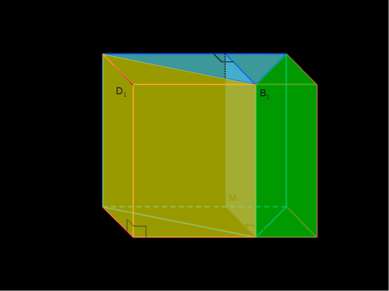A B A1 C1 E1 D E M M1 Рассмотрим произвольную треугольную прямую призму ABCA1B1C1. 1) Разобьем призму на две прямые треугольные призмы ABMA1B1M1 и BCMB1C1M1 плоскостью, проходящей через высоту основания B1M1 и боковое ребро BB1. 2) Достроим данную призму до прямоугольного параллелепипеда ADECA1D1C1E1. C 3) Получили ещё две прямые треугольные призмы ADBA1D1B1 и BECB1E1C1. D1 B1
Cлайд 6
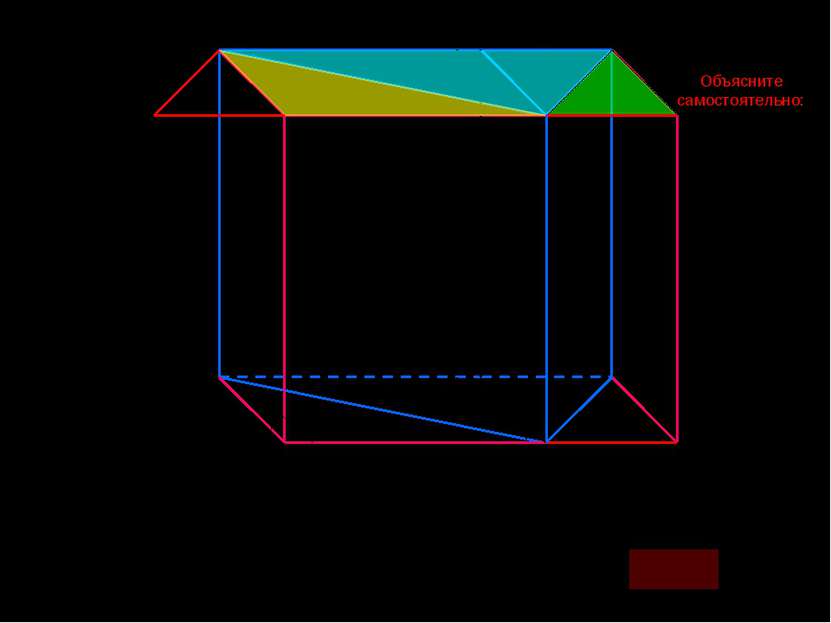
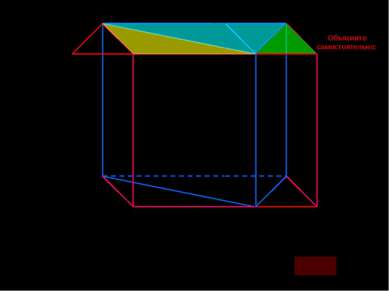A B C A1 B1 C1 D1 E1 D E M M1 Нетрудно заметить, что объем треугольной призмы в два раза меньше объема прямоугольного параллелепипеда, т.е. H B1 B M1 M Объясните самостоятельно: F1 F
Cлайд 7
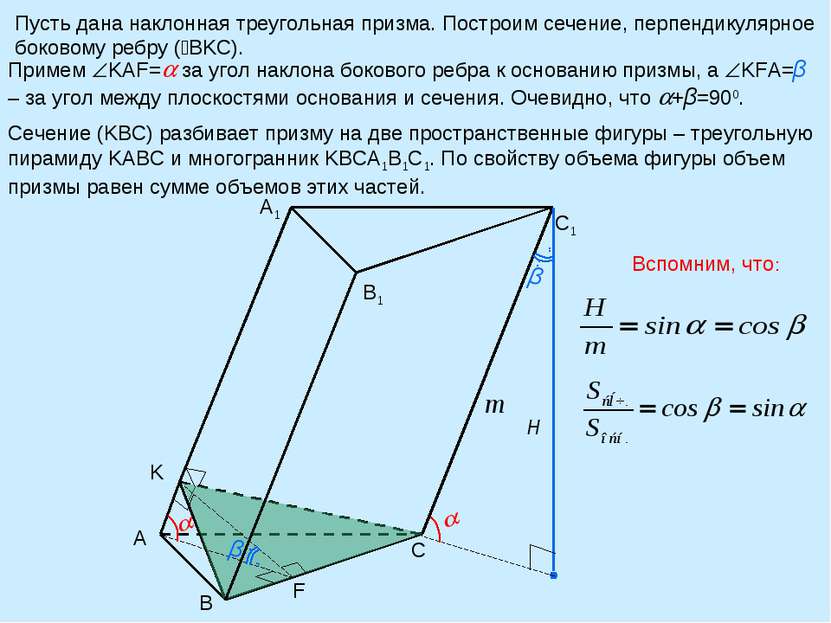
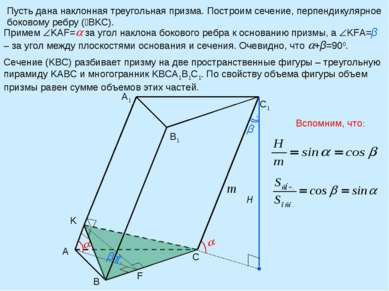Пусть дана наклонная треугольная призма. Построим сечение, перпендикулярное боковому ребру ( BKC). A B C K A1 B1 C1 β F Примем KAF= за угол наклона бокового ребра к основанию призмы, а KFA=β – за угол между плоскостями основания и сечения. Очевидно, что +β=900. Сечение (KBC) разбивает призму на две пространственные фигуры – треугольную пирамиду KABC и многогранник KBCA1B1C1. По свойству объема фигуры объем призмы равен сумме объемов этих частей. Вспомним, что: H m β
Cлайд 8
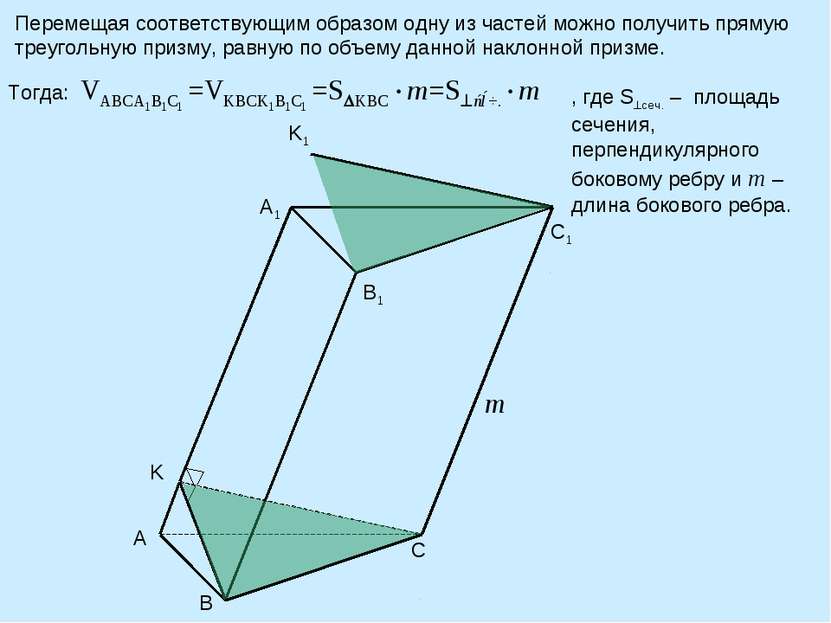
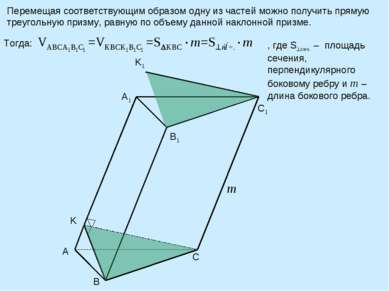Перемещая соответствующим образом одну из частей можно получить прямую треугольную призму, равную по объему данной наклонной призме. B C K A1 B1 C1 A K1 m Тогда: , где S сеч. – площадь сечения, перпендикулярного боковому ребру и m –длина бокового ребра.
Cлайд 9
С учетом вспомненных соотношений, получим: B C K B1 C1 K1 m
Cлайд 10
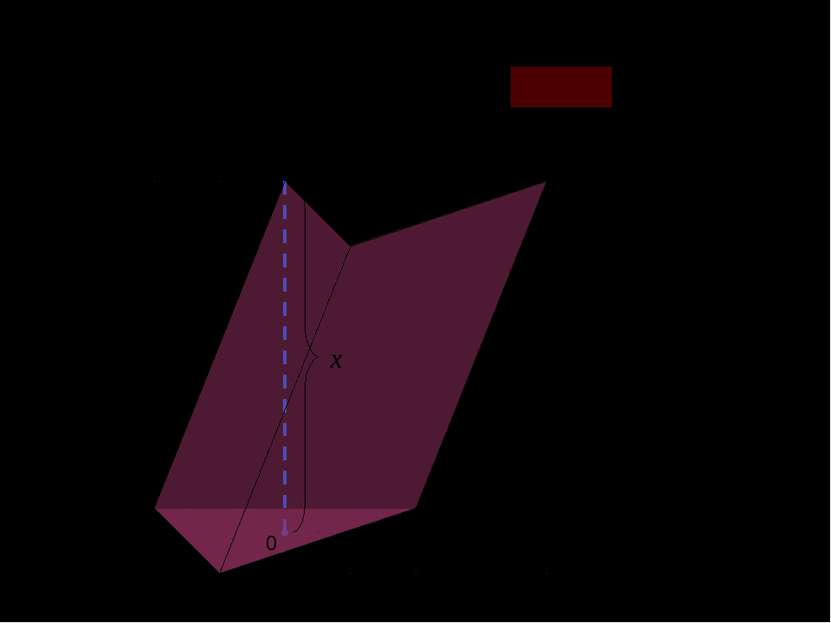
A B C B1 H A1 C1 Если применить метод бесконечных интегральных сумм, то получится: x x x [ 0; H ] 0
Cлайд 11
H Рассмотрим произвольную n-угольную призму A1A2…An B1B2…Bn. Разобьем её на (n–2) треугольные призмы, полученные при проведении диагональных сечений из вершины A1. По свойству объема: A1 A2 An B1 B2 Bn
Cлайд 12
Итак, для любой n-угольной призмы: ИЛИ ,где Sосн. – площадь основания призмы, S сеч. – площадь перпендикулярного сечения, H – высота призмы, m – длина бокового ребра призмы.
