X
Код презентации скопируйте его
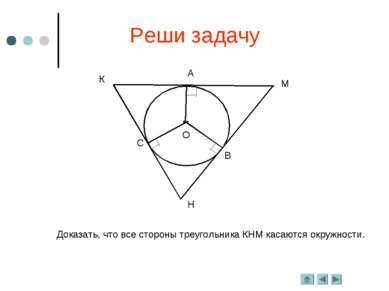
Касательная к окружности 7 класс
Скачать эту презентациюПрезентация на тему Касательная к окружности 7 класс
Скачать эту презентациюCлайд 4
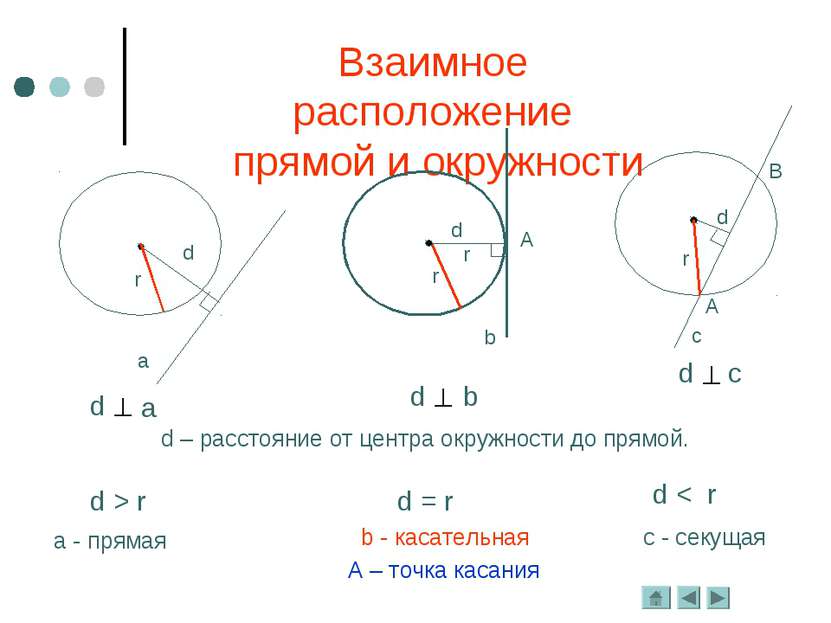
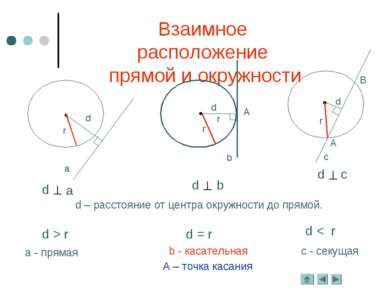
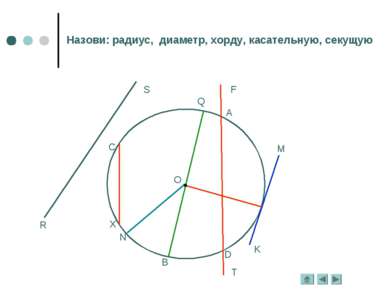
 Теорема. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания. Дано: Окр.(О;r), р – касательная, А – точка касания. Доказательство: А – точка касания, О – центр окружности, значит, ОА – радиус. Пусть касательная р не перпендикулярна ОА, тогда радиус ОА является наклонной к прямой р. Тогда перпендикуляр, проведённый из точки О к прямой р, меньше наклонной ОА, т. е. расстояние от центра окружности меньше радиуса. Значит, прямая р и окружность будут иметь две общих точки, но это противоречит условию: р – касательная, т. е. она имеет с окружностью одну общую точку. Следовательно, предположение, что р не перпендикулярна ОА неверно. Касательная к окружности Определение. Прямая, имеющая с окружностью одну общую точку, называется касательной.
Теорема. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания. Дано: Окр.(О;r), р – касательная, А – точка касания. Доказательство: А – точка касания, О – центр окружности, значит, ОА – радиус. Пусть касательная р не перпендикулярна ОА, тогда радиус ОА является наклонной к прямой р. Тогда перпендикуляр, проведённый из точки О к прямой р, меньше наклонной ОА, т. е. расстояние от центра окружности меньше радиуса. Значит, прямая р и окружность будут иметь две общих точки, но это противоречит условию: р – касательная, т. е. она имеет с окружностью одну общую точку. Следовательно, предположение, что р не перпендикулярна ОА неверно. Касательная к окружности Определение. Прямая, имеющая с окружностью одну общую точку, называется касательной.
Cлайд 6
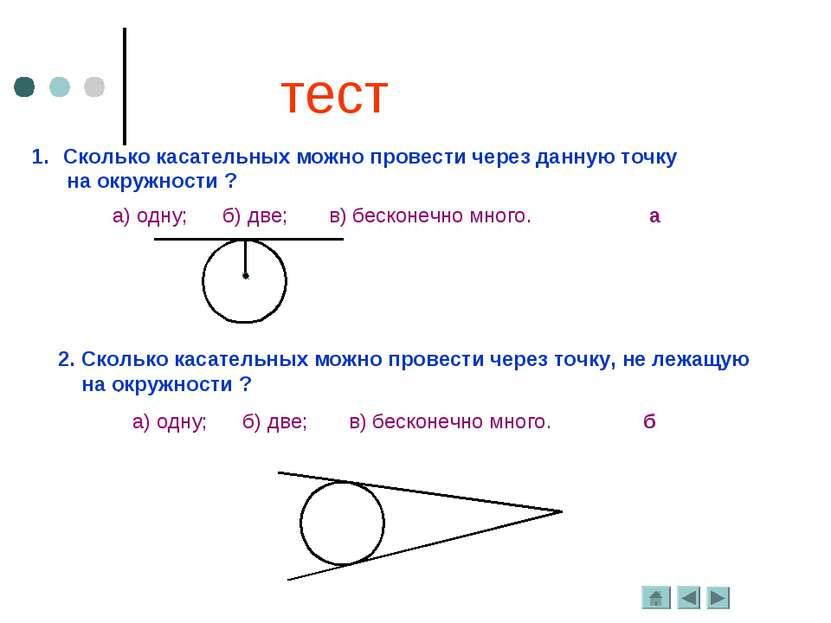
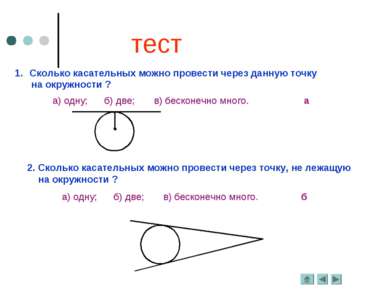 тест Сколько касательных можно провести через данную точку на окружности ? а) одну; б) две; в) бесконечно много. 2. Сколько касательных можно провести через точку, не лежащую на окружности ? а а) одну; б) две; в) бесконечно много. б .
тест Сколько касательных можно провести через данную точку на окружности ? а) одну; б) две; в) бесконечно много. 2. Сколько касательных можно провести через точку, не лежащую на окружности ? а а) одну; б) две; в) бесконечно много. б .
Cлайд 7
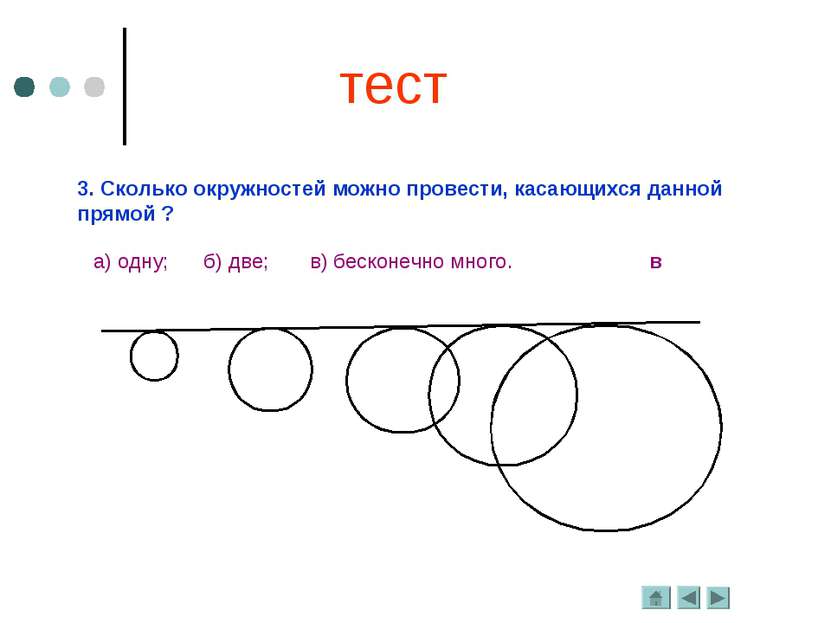
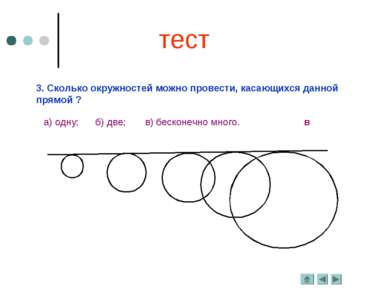 3. Сколько окружностей можно провести, касающихся данной прямой ? а) одну; б) две; в) бесконечно много. в тест
3. Сколько окружностей можно провести, касающихся данной прямой ? а) одну; б) две; в) бесконечно много. в тест
Cлайд 8
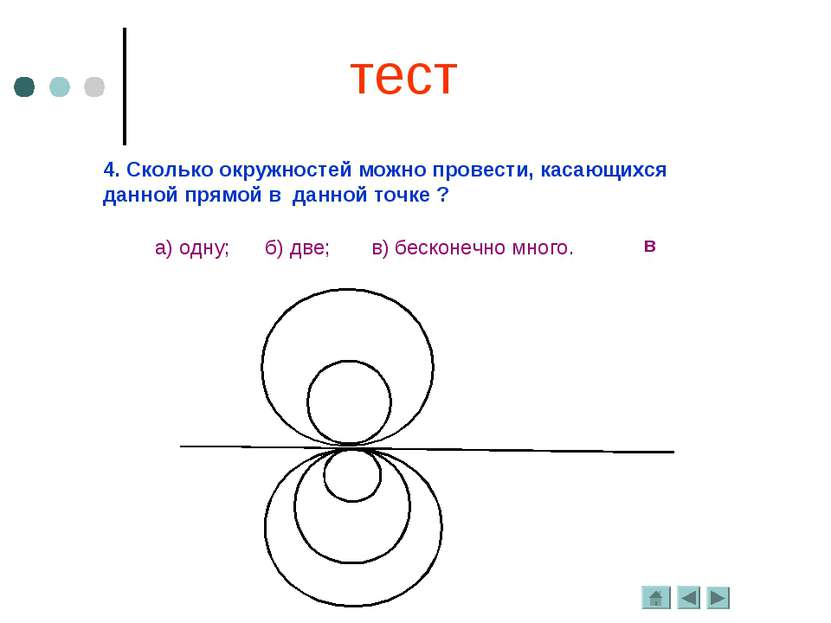
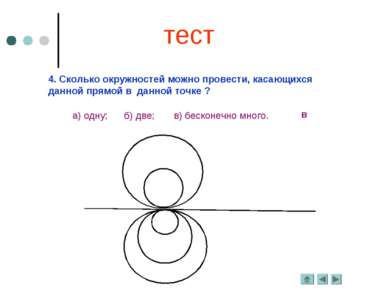 4. Сколько окружностей можно провести, касающихся данной прямой в данной точке ? в а) одну; б) две; в) бесконечно много. тест
4. Сколько окружностей можно провести, касающихся данной прямой в данной точке ? в а) одну; б) две; в) бесконечно много. тест
Cлайд 9
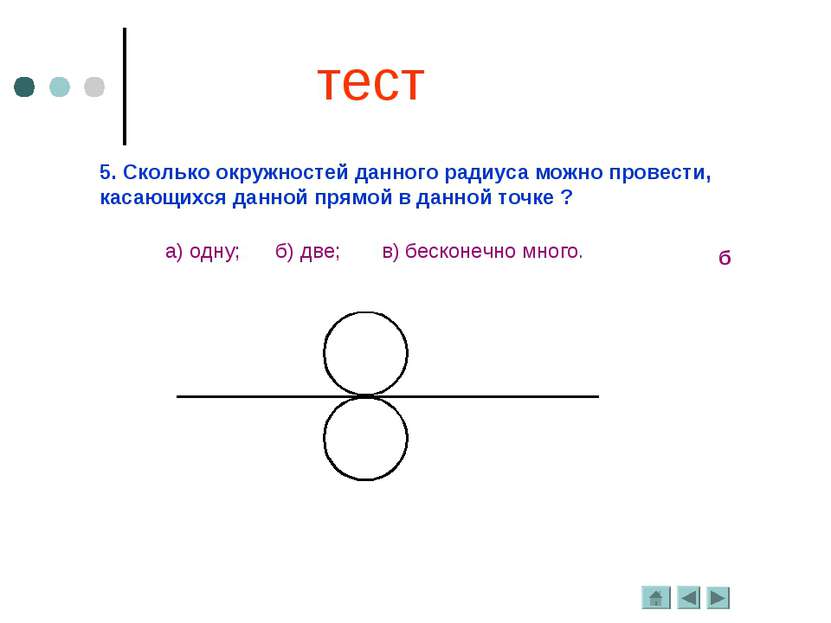
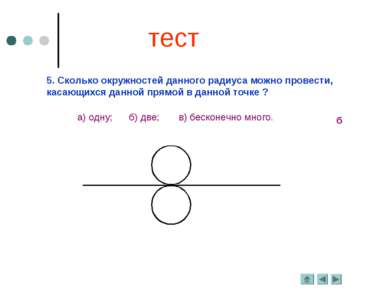 5. Сколько окружностей данного радиуса можно провести, касающихся данной прямой в данной точке ? а) одну; б) две; в) бесконечно много. б тест
5. Сколько окружностей данного радиуса можно провести, касающихся данной прямой в данной точке ? а) одну; б) две; в) бесконечно много. б тест
Cлайд 11
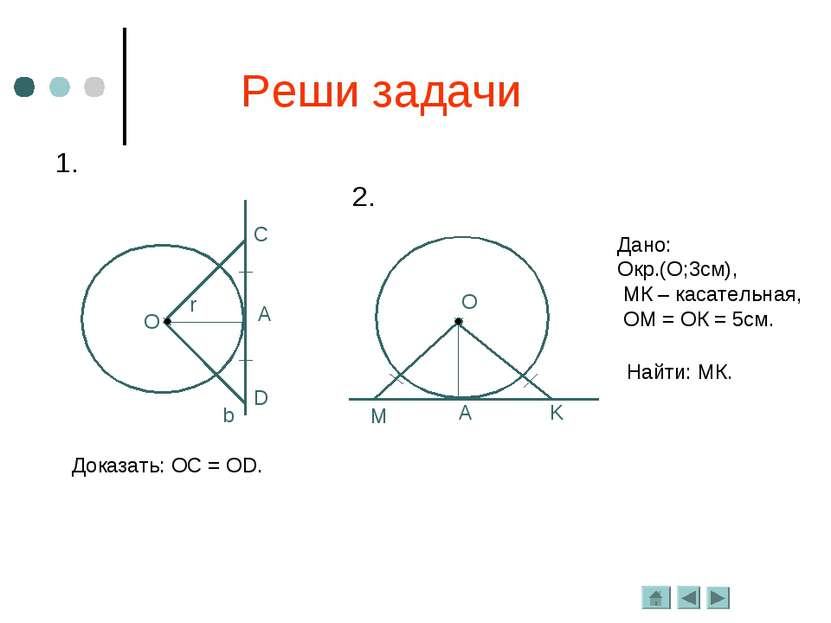
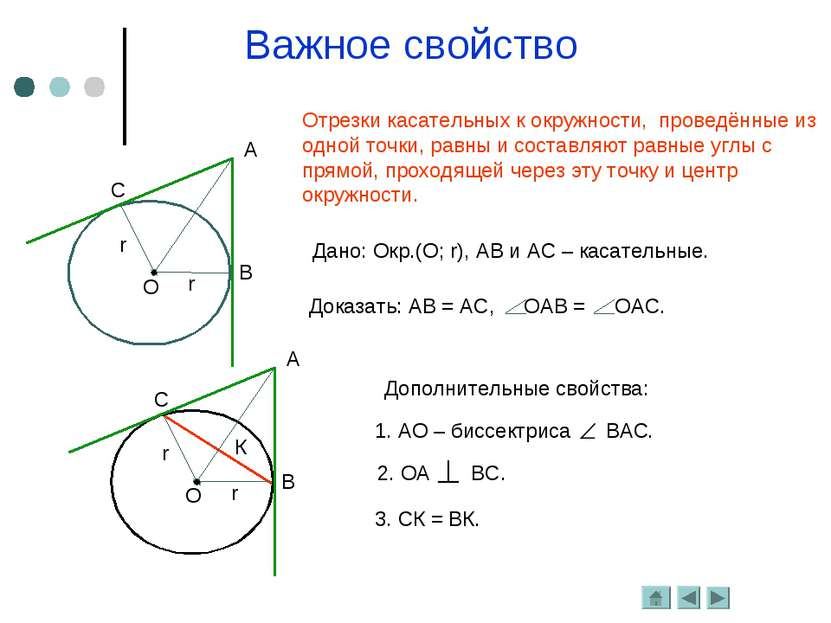
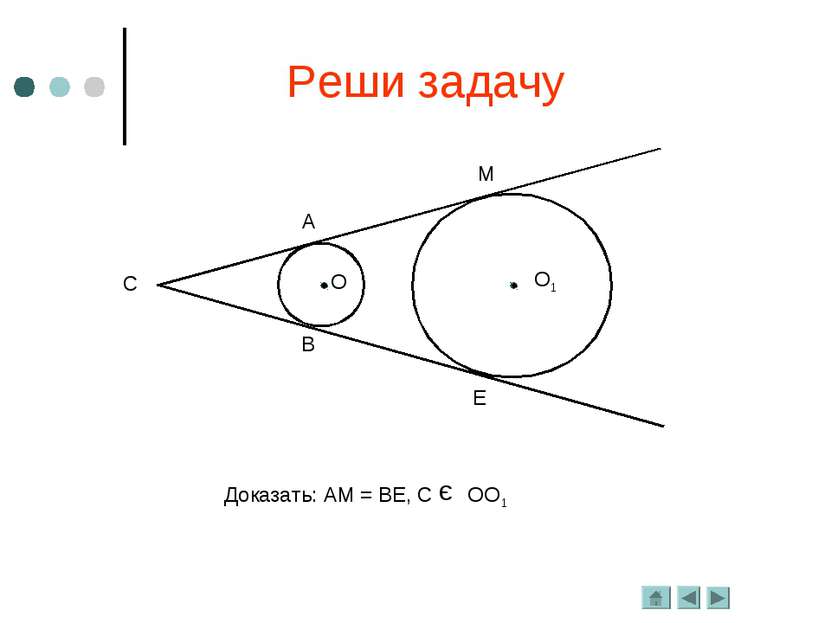
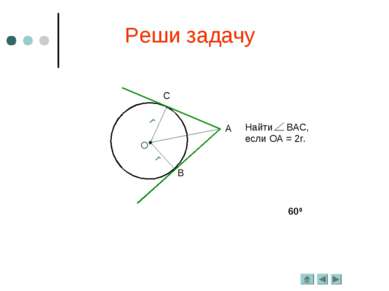
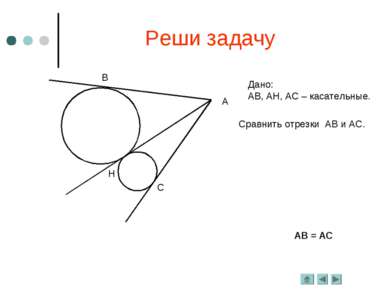
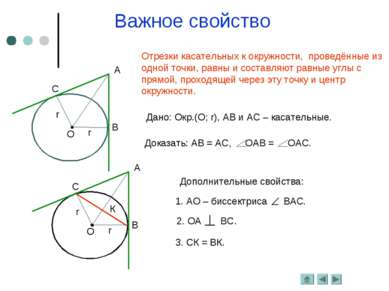 Важное свойство Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. Дано: Окр.(О; r), АВ и АС – касательные. Дополнительные свойства: 3. СК = ВК.
Важное свойство Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. Дано: Окр.(О; r), АВ и АС – касательные. Дополнительные свойства: 3. СК = ВК.
Cлайд 17
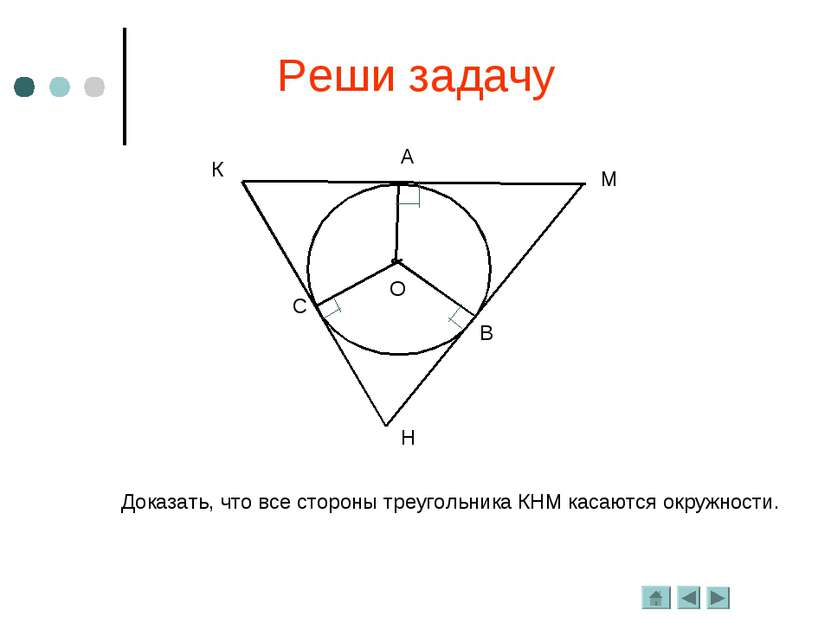
 Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной. (теорема, обратная к свойству касательной) Признак касательной Доказать: АВ – касательная. Доказательство: и, следовательно, прямая и окружность имеют только одну общую точку. По определению касательной и будет прямая АВ.
Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной. (теорема, обратная к свойству касательной) Признак касательной Доказать: АВ – касательная. Доказательство: и, следовательно, прямая и окружность имеют только одну общую точку. По определению касательной и будет прямая АВ.