X
Код презентации скопируйте его
Призма 9 класс
Скачать эту презентациюПрезентация на тему Призма 9 класс
Скачать эту презентациюCлайд 2
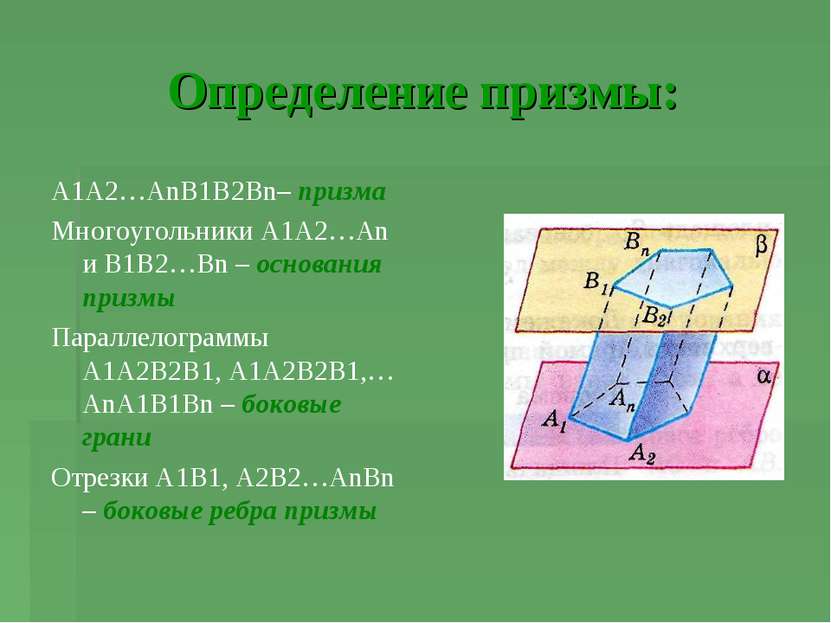
 Определение призмы: А1А2…АnВ1В2Вn– призма Многоугольники А1А2…Аn и В1В2…Вn – основания призмы Параллелограммы А1А2В2В1, А1А2В2В1,… АnА1В1Вn – боковые грани Отрезки А1В1, А2В2…АnBn – боковые ребра призмы
Определение призмы: А1А2…АnВ1В2Вn– призма Многоугольники А1А2…Аn и В1В2…Вn – основания призмы Параллелограммы А1А2В2В1, А1А2В2В1,… АnА1В1Вn – боковые грани Отрезки А1В1, А2В2…АnBn – боковые ребра призмы
Cлайд 4
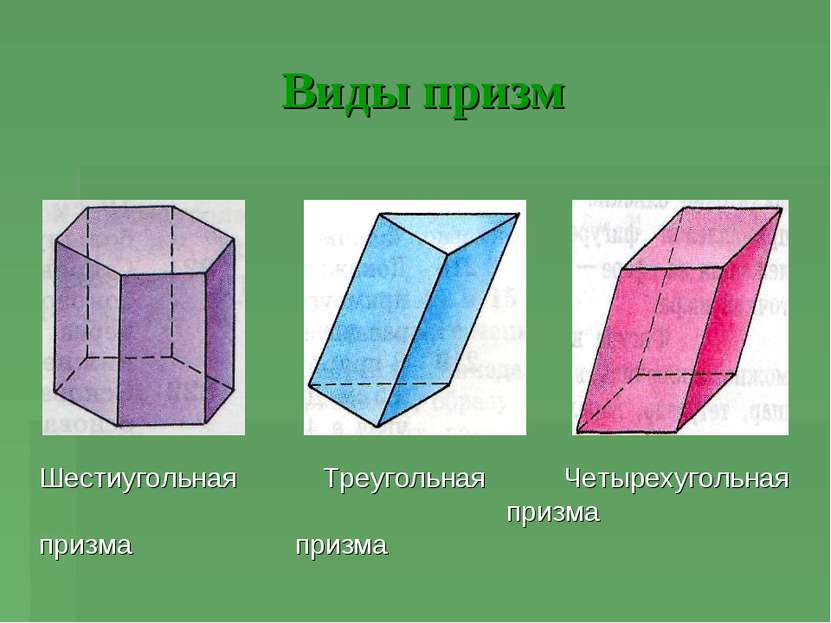
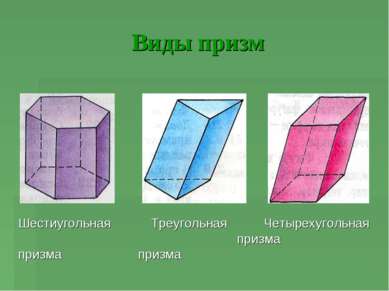
 Наклонная и прямая призма Если боковые ребра призмы перпендикулярны основаниям то призма называется прямой, в противном случае – наклонной.
Наклонная и прямая призма Если боковые ребра призмы перпендикулярны основаниям то призма называется прямой, в противном случае – наклонной.
Cлайд 5
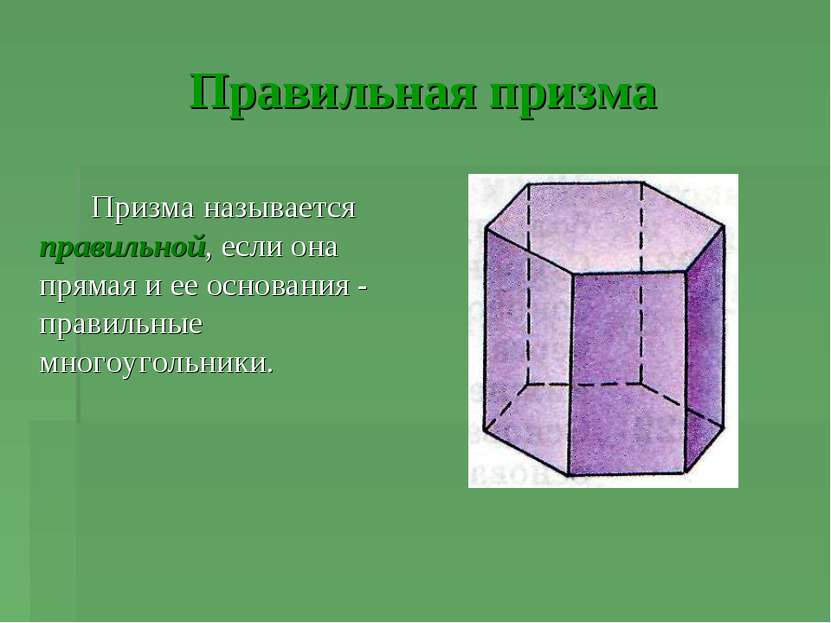
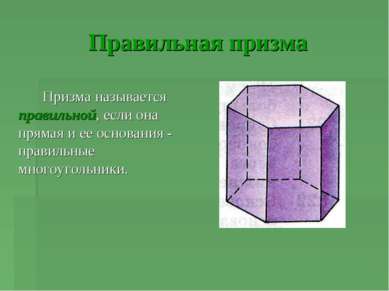 Правильная призма Призма называется правильной, если она прямая и ее основания - правильные многоугольники.
Правильная призма Призма называется правильной, если она прямая и ее основания - правильные многоугольники.
Cлайд 7
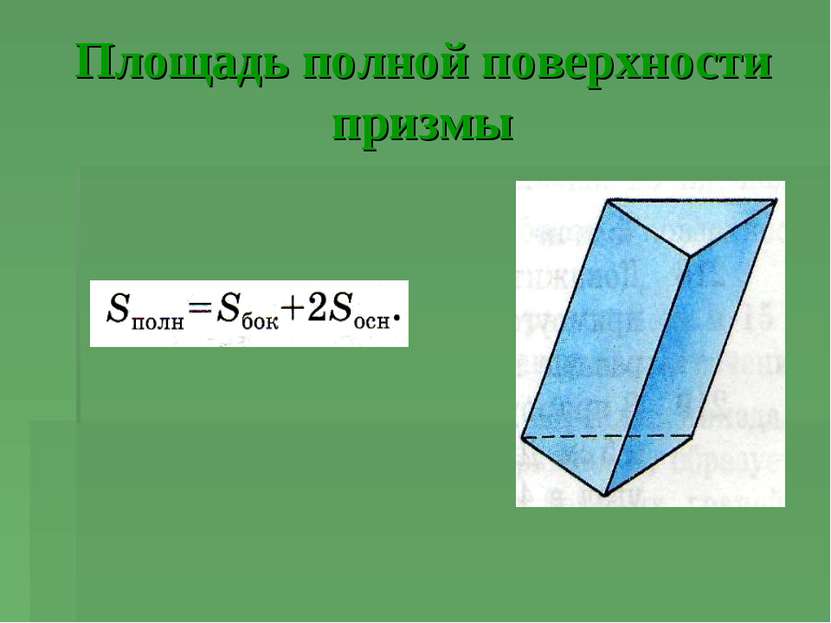
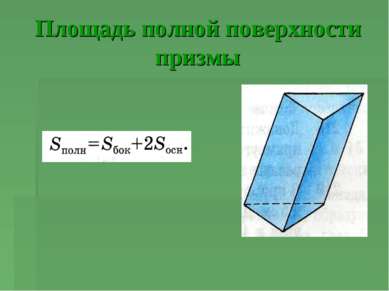
 Площадь боковой поверхности призмы Теорема Площадь боковой поверхности прямой призмы равна половине произведения периметра основания на высоту призмы.
Площадь боковой поверхности призмы Теорема Площадь боковой поверхности прямой призмы равна половине произведения периметра основания на высоту призмы.
Cлайд 8
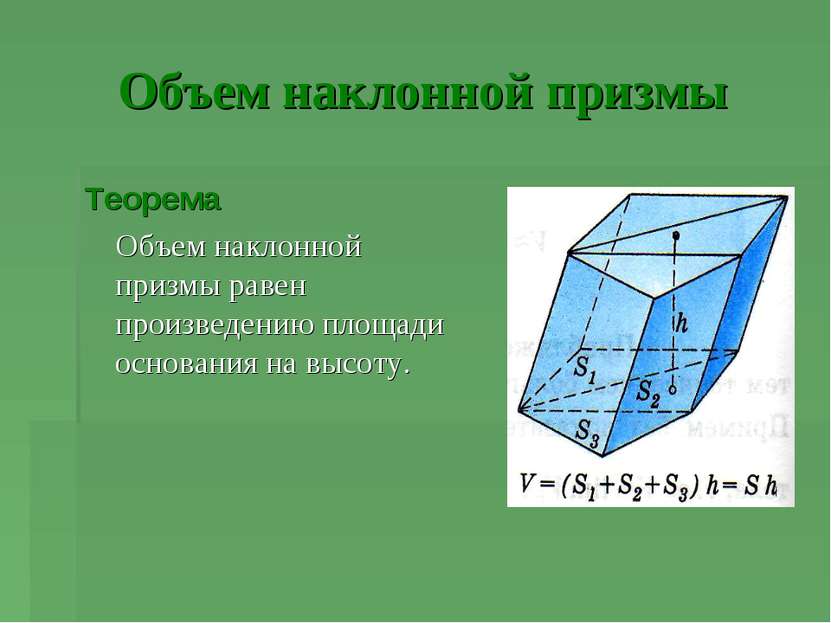
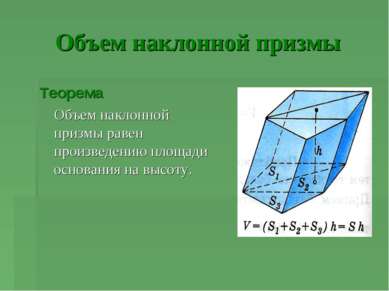 Объем наклонной призмы Теорема Объем наклонной призмы равен произведению площади основания на высоту.
Объем наклонной призмы Теорема Объем наклонной призмы равен произведению площади основания на высоту.
Cлайд 9
 Доказательство Докажем сначала теорему для треугольной призмы, а затем — для произвольной призмы. 1. Рассмотрим треугольную призму с объ емом V, площадью основания S и высотой h. Отметим точку О на одном из оснований призмы и направим ось Ох перпендикулярно к основаниям. Рассмотрим сечение призмы плоскостью, перпендикуляр ной к оси Ох и, значит, параллельной плоскости основания. Обозначим буквой х абсциссу точки пересе чения этой плоскости с осью Ох, а через S (х) — площадь получившегося сечения. Докажем, что площадь S (х) равна площади S основания призмы. Для этого заметим, что треуголь ники ABC (основание призмы) и А1B1С1 (сечение призмы рассматриваемой плоскостью) равны. В самом деле, четырехугольник АA1BB1 — параллелограмм (отрезки АА1 и ВВ1 равны и параллельны), поэтому А1В1=АВ. Аналогично доказывается, что В1С1=ВС и А1С1=АС. Итак, треугольники А1В1С1 и ABC равны по трем сторонам. Следовательно, S(x)=S. Применяя теперь основную формулу для вычисления объемов тел при а=0 и b=h, получаем
Доказательство Докажем сначала теорему для треугольной призмы, а затем — для произвольной призмы. 1. Рассмотрим треугольную призму с объ емом V, площадью основания S и высотой h. Отметим точку О на одном из оснований призмы и направим ось Ох перпендикулярно к основаниям. Рассмотрим сечение призмы плоскостью, перпендикуляр ной к оси Ох и, значит, параллельной плоскости основания. Обозначим буквой х абсциссу точки пересе чения этой плоскости с осью Ох, а через S (х) — площадь получившегося сечения. Докажем, что площадь S (х) равна площади S основания призмы. Для этого заметим, что треуголь ники ABC (основание призмы) и А1B1С1 (сечение призмы рассматриваемой плоскостью) равны. В самом деле, четырехугольник АA1BB1 — параллелограмм (отрезки АА1 и ВВ1 равны и параллельны), поэтому А1В1=АВ. Аналогично доказывается, что В1С1=ВС и А1С1=АС. Итак, треугольники А1В1С1 и ABC равны по трем сторонам. Следовательно, S(x)=S. Применяя теперь основную формулу для вычисления объемов тел при а=0 и b=h, получаем
Cлайд 10
 2. Докажем теперь теорему для произвольной призмы с высотой h и площадью основания S. Такую призму можно разбить на треугольные призмы с общей высотой h. Выразим объем каждой треуголь ной призмы по доказанной нами формуле и сложим эти объемы. Вынося за скобки общий множитель h, получим в скобках сумму площадей оснований треугольных призм, т. е. площадь S основания исходной призмы. Таким образом, объем исходной призмы равен S * h. Теорема доказана.
2. Докажем теперь теорему для произвольной призмы с высотой h и площадью основания S. Такую призму можно разбить на треугольные призмы с общей высотой h. Выразим объем каждой треуголь ной призмы по доказанной нами формуле и сложим эти объемы. Вынося за скобки общий множитель h, получим в скобках сумму площадей оснований треугольных призм, т. е. площадь S основания исходной призмы. Таким образом, объем исходной призмы равен S * h. Теорема доказана.