X
Код презентации скопируйте его
Комбинаторика Правило сложения Правило умножения
Скачать эту презентацию
Презентация на тему Комбинаторика Правило сложения Правило умножения
Скачать эту презентациюCлайд 1
Комбинаторика Правило сложения Правило умножения
Cлайд 2
Задача №1. На одной полке книжного шкафа стоит 30 различных книг, а на другой – 40 различных книг (не такие как на первой). Сколькими способами можно выбрать одну книгу. Решение: 30 + 40 = 70 (способами).
Cлайд 3
Правило суммы Если пересечение конечных множеств А и В пусто, то число элементов в их объединении равно сумме чисел элементов множеств А и В :
Cлайд 4
Задача № 2 При формировании экипажа космического корабля имеется 10 претендентов на пост командира, 20 – на пост инженера и 25 – на пост космонавта. Сколькими способами можно выбрать одну из кандидатур или командира, или инженера, или космонавта, если не один кандидат не претендует одновременно на два поста?
Cлайд 5
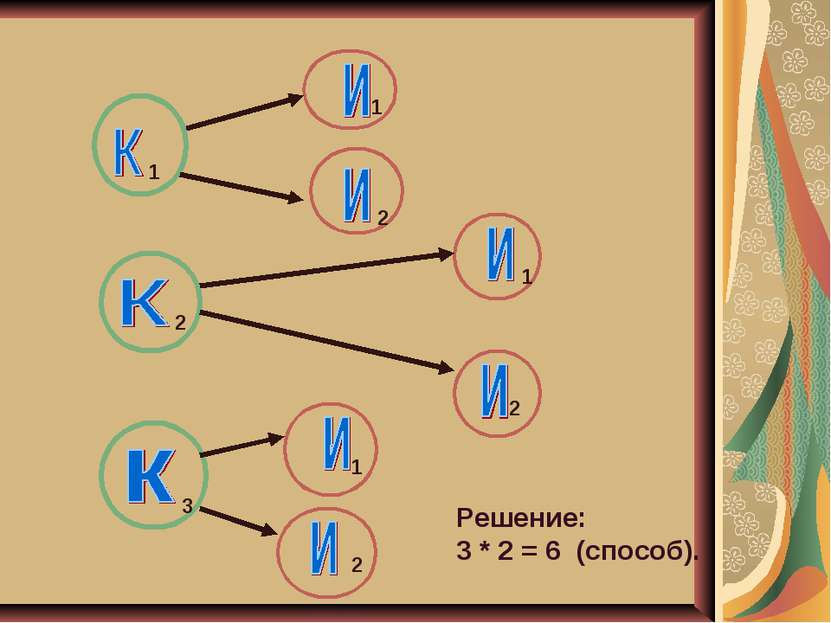
Задача № 3 Пусть существует три кандидата на пост командира и 2 на пост инженера. Сколькими способами можно сформировать экипаж корабля, состоящий из командира и инженера?
Cлайд 6
1 1 1 1 2 3 2 2 2 Решение: 3 * 2 = 6 (способ).
Cлайд 7
Правило умножения. Если множества А и В конечны, то число N возможных пар (а; в), где а из А, в из В равно произведению чисел элементов этих множеств: N = n (A) *n (B)
Cлайд 8
Задача № 2 Сколькими способами можно выбрать в столовой обед из трех блюд из предложенных двух первых, трех вторых блюд и двух видов десерта.
Cлайд 9
Работу приготовил ученик 11 б класса Ушаков Глеб учитель Кинзябулатова Л.А.
