Решение простейших логарифмических логарифмических уравнений

Скачать эту презентацию

Получить код Увеличить

Решение простейших логарифмических уравнений. К уроку по алгебре и началам ан...

Решить уравнение: Log2 (x+3)=2 1.Найдём ОДЗ, учитывая , что логарифм определё...

2.Решим уравнение: Log2(x+3)=2 , 2 = Log222= Log2 4 Log2(x+3)=Log24 X+3=4 X=4...

Решить уравнение: Log0,3(4-x)=Log0,3(x+2). 1. Найдём ОДЗ уравнения: Log0,3(4-...

2. Решаем уравнение: Log0,3(4-x)=Log0,3(2+x) 4 - x = 2+x -2x=2-4 -2x = -2 X=1

Решить уравнение: Logе(3х+7)- 2Loge(x+1)=0.

2.Решаем уравнение: Logе(3х+7)- 2Loge(x+1)=0. Logе(3х+7)= 2Loge(x+1), 2Loge(x...

Решить уравнение: 3Log3(1-x2)-Log3(1-x2)=4

1.Найдём ОДЗ: 3Log3(1-x2 ) - Log3(1-x2) =4. 1 - x2 >0, X2 < 1, |x|

2.Решим уравнение: 3Log3 2(1-x2)+Log3(1-x2) – 4 = 0, Пусть Log3(1-x2)= t, тог...

Уравнения для самостоятельного решения. Вариант 1. 1.log8(3x-2)=2 2.log0,99(5...

1 22

Презентация на тему Решение простейших логарифмических логарифмических уравнений

Скачать эту презентацию

Cлайд 1

Решение простейших логарифмических уравнений. К уроку по алгебре и началам анализа учителя математики Варавва Н.А. МБОУ гимназия № 72 имени академика В.П.Глушко города Краснодара

Cлайд 2

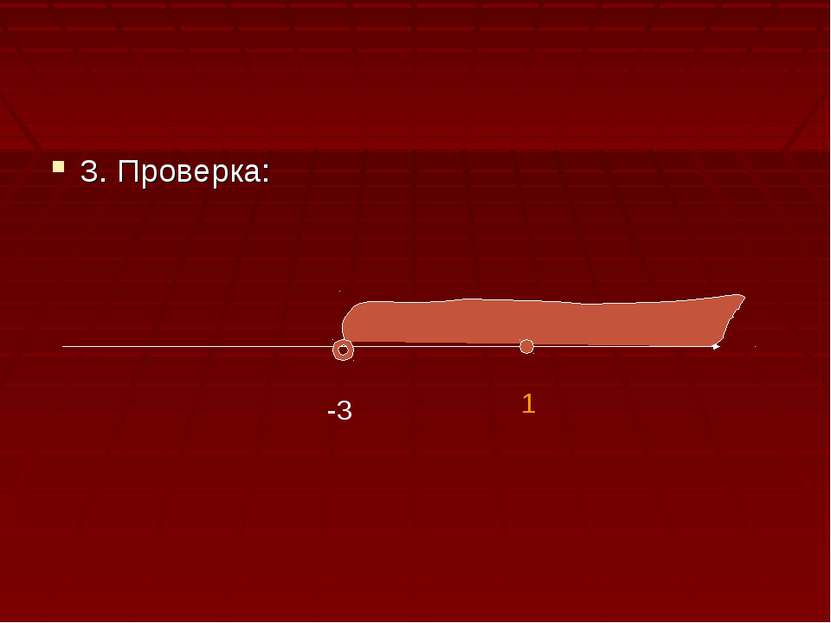
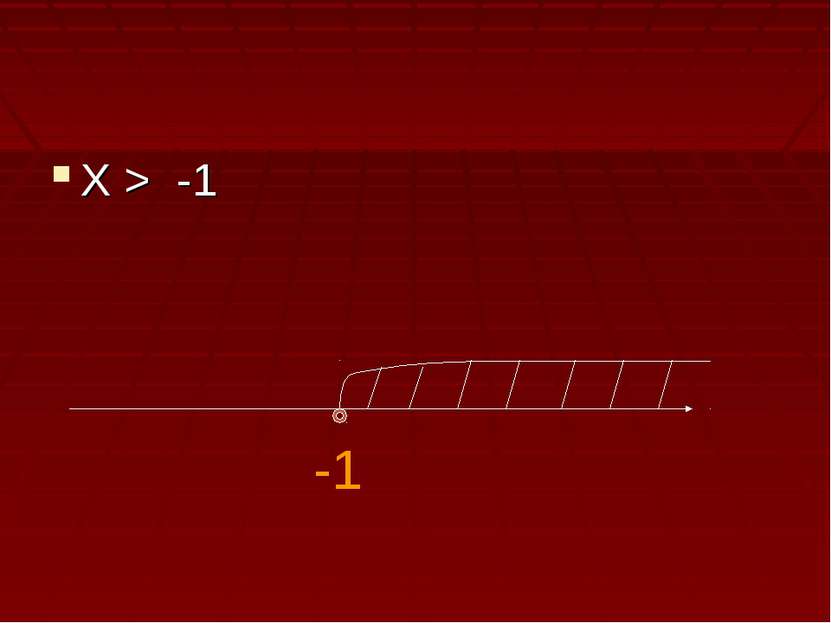
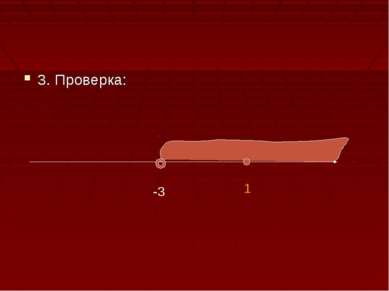
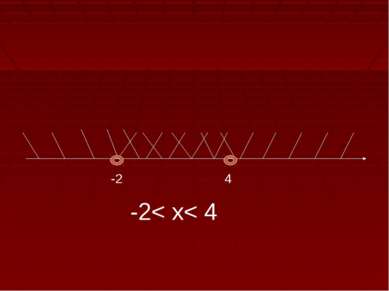
Решить уравнение: Log2 (x+3)=2 1.Найдём ОДЗ, учитывая , что логарифм определён только для положительных чисел. Х+3>0 X>-3 -3

Cлайд 3

2.Решим уравнение: Log2(x+3)=2 , 2 = Log222= Log2 4 Log2(x+3)=Log24 X+3=4 X=4-3 X=1

Cлайд 4

3. Проверка: -3 1

Cлайд 5

Ответ:1.

Cлайд 6

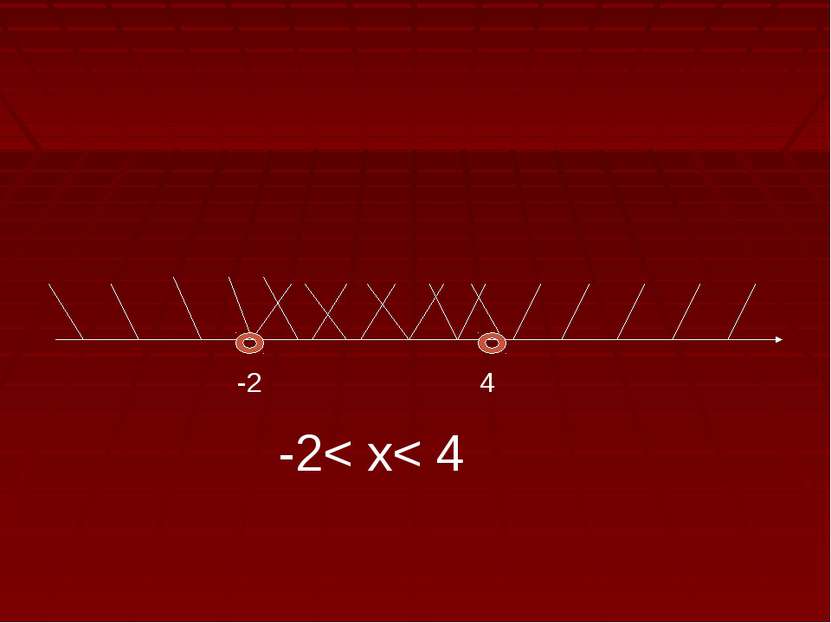
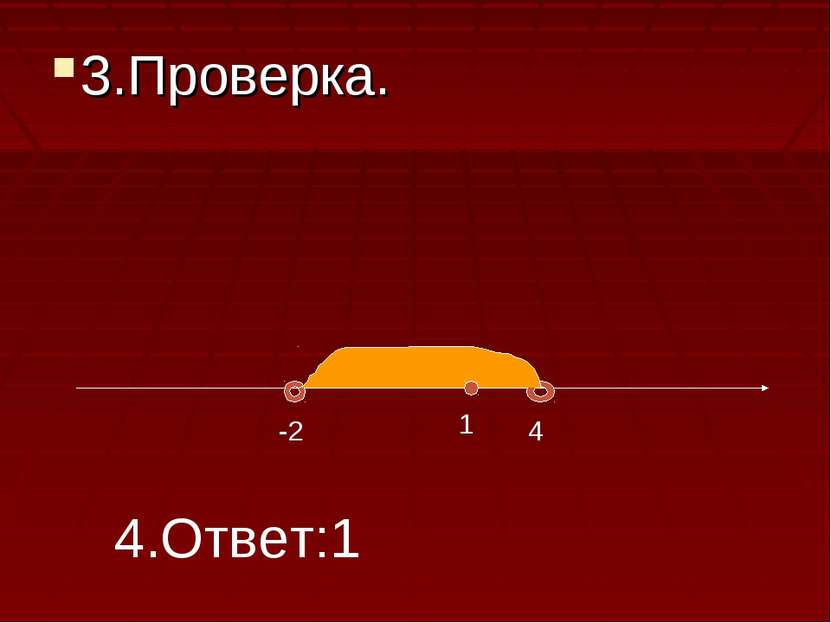
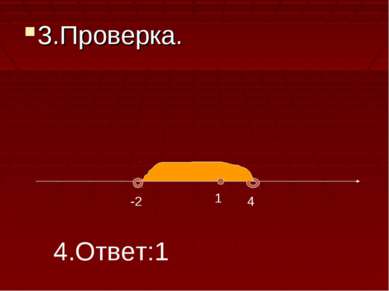
Решить уравнение: Log0,3(4-x)=Log0,3(x+2). 1. Найдём ОДЗ уравнения: Log0,3(4-x)=Log0,3 (x+2)

Cлайд 7

-2 4 -2< x< 4

Cлайд 8

2. Решаем уравнение: Log0,3(4-x)=Log0,3(2+x) 4 - x = 2+x -2x=2-4 -2x = -2 X=1

Cлайд 9

3.Проверка. -2 4 1 4.Ответ:1

Cлайд 10

Решить уравнение: Logе(3х+7)- 2Loge(x+1)=0.

Cлайд 11

1.Найдём ОДЗ: Logе(3х+7)- 2Loge(x+1)=0.

Cлайд 12

X > -1 -1

Cлайд 13

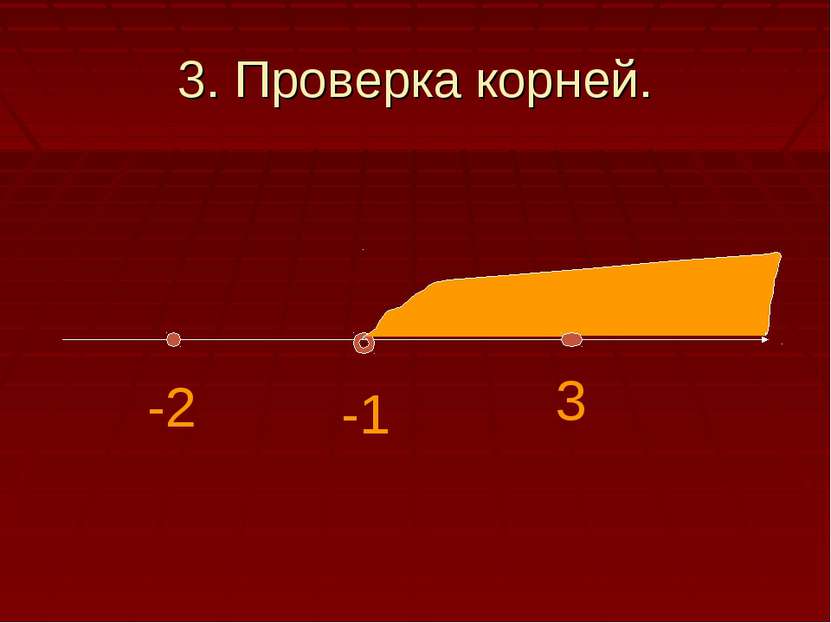
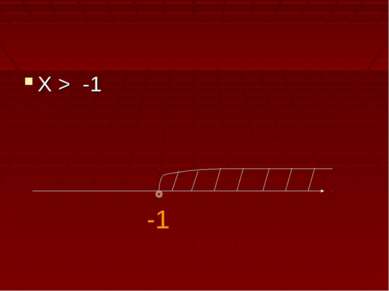
2.Решаем уравнение: Logе(3х+7)- 2Loge(x+1)=0. Logе(3х+7)= 2Loge(x+1), 2Loge(x+1)= Loge(x+1)2 Loge(3x+7)=Loge(x+1)2 3x+7=(x+1)2 3x+7=x2 +2x +1 X2 +2x +1-3x -7=0 X2 –x – 6 =0 По теореме обратной Виета:х1 =3, х2 =-2

Cлайд 14

3. Проверка корней. -1 3 -2

Cлайд 15

Ответ.3

Cлайд 16

Решить уравнение: 3Log3(1-x2)-Log3(1-x2)=4

Cлайд 17

1.Найдём ОДЗ: 3Log3(1-x2 ) - Log3(1-x2) =4. 1 - x2 >0, X2 < 1, |x|

Cлайд 18

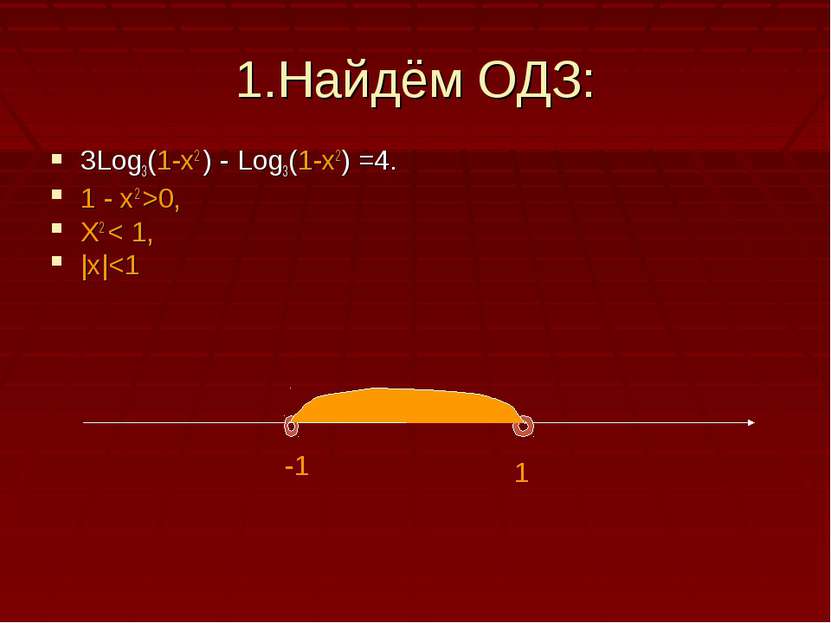
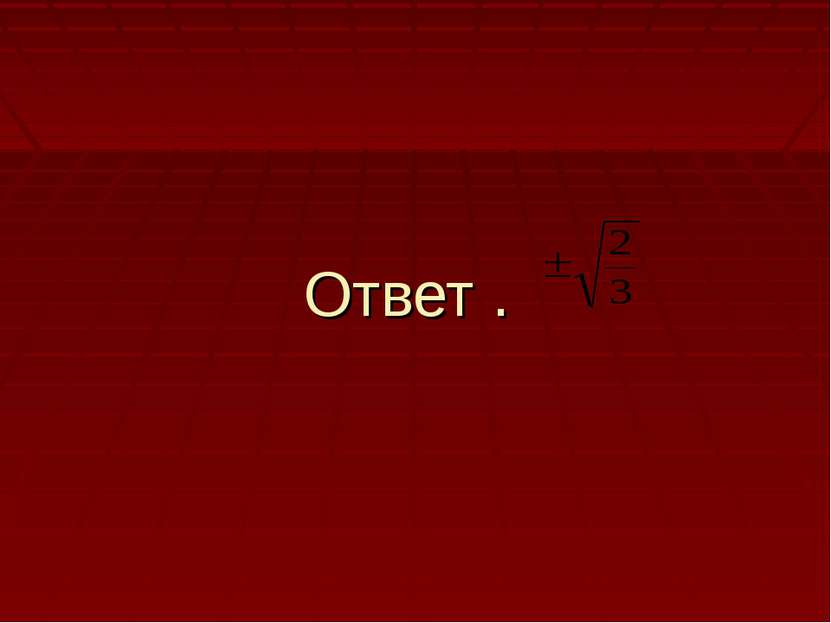
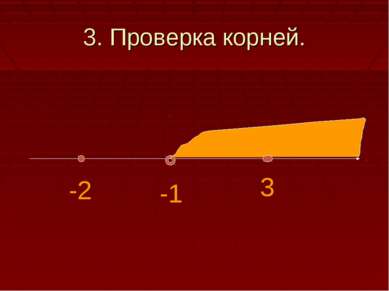
2.Решим уравнение: 3Log3 2(1-x2)+Log3(1-x2) – 4 = 0, Пусть Log3(1-x2)= t, тогда уравнение примет вид: 3t2 - t -4 =0, т.к. а+в+с=0 , то t1= -1, t2 =-c\a= 4\3. Получим: Log3(1-x2)=-1 или Log3(1-x2)=4/3 Log3(1-x2)=Log31/3 1- х2 = 34/3 1-x2 =1/3 х2 = 1-34/3

Cлайд 19

3.Проверка. -1 1

Cлайд 20

Ответ .

Cлайд 21

Уравнения для самостоятельного решения. Вариант 1. 1.log8(3x-2)=2 2.log0,99(5x-1)=log0,99(3x+7) 3.log54+log5(x-1)=log58 4.10lg(x-6)=x2 -12x +36 5. ln (x2-x)=ln(2x+4) Вариант 2. 1.log7(5x+2)=1 2.lg(6x+1)=lg(-x+8) 3.log49+log4(x+1)=log43 4.eln(x-2)=x2 +6x -8 5. log2 (x2+3x)=log 2(x+3)

Cлайд 22