X
Код презентации скопируйте его
Решение неравенств с одной переменной 8 класс
Скачать эту презентацию
Презентация на тему Решение неравенств с одной переменной 8 класс
Скачать эту презентациюCлайд 1
* учитель математики МОУ «Ворошиловоградская основная общеобразовательная школа» Колосов А.П. 2010 год
Cлайд 2
* 1) 0,5 < 0,7 на 4 Ответ: 2 < 2,8 1 > 1 на - 12 3 4 Ответ: -4 < -3 3) 3k< 10 на 2 Ответ: 6k < 20 4) -4d > -7 на -3 Ответ: 12d < 21
Cлайд 3
*
Cлайд 4
*
Cлайд 5
*
Cлайд 6
* 1. Если x > 2 и y > 3, то xy > 6 ? Ответ: Утверждение верно 2. Если x < -5 и y < 4 то x + y < 0 ? Ответ: Утверждение верно РЕШЕНИЕ: при сложении неравенств одинакового знака x
Cлайд 7
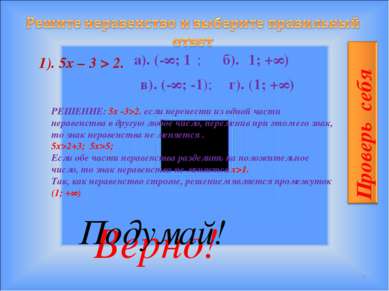* 1). 5x – 3 > 2. г). (1; +∞) РЕШЕНИЕ: 5х -3>2. если перенести из одной части неравенства в другую любое число, переменив при этом его знак, то знак неравенства не меняется . 5х>2+3; 5х>5; Если обе части неравенства разделить на положительное число, то знак неравенства не меняется x>1. Так, как неравенство строгое, решением является промежуток (1; +∞) Верно! Подумай!
Cлайд 8
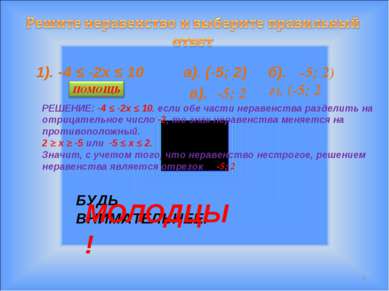* 1). -4 ≤ -2х ≤ 10 а). (-5; 2) б). ⦋-5; 2) г). (-5; 2⦌ в). ⦋-5; 2⦌ РЕШЕНИЕ: -4 ≤ -2х ≤ 10. если обе части неравенства разделить на отрицательное число -2, то знак неравенства меняется на противоположный. 2 ≥ х ≥ -5 или -5 ≤ х ≤ 2. Значит, с учетом того, что неравенство нестрогое, решением неравенства является отрезок ⦋-5; 2⦌ БУДЬ ВНИМАТЕЛЬНЕЕ! МОЛОДЦЫ!
Cлайд 9
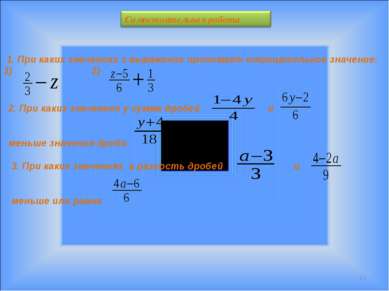
* 1). Докажите, что: Если (х-2)(х+3)> (х+2)(х-3), то х > 2; Если (х+1)(х+2)>(х+2)(х-3), то х < 0 2). Решите неравенство 7(х+1)+10>11-7(2-х) 5(1-х)-4>7-5х 3). Решите задачу Сторона прямоугольного пенала больше 5 см, вторая сторона больше первой в 3 раза. Правильно ли, что периметр пенала больше 40 см? Одна сторона треугольника равна 7 см, другая –10 см. какова наибольшая длина третьей стороны треугольника в целых числах?
Cлайд 10
* 1). Доказательство: (х-2)(х+3)>(х+2)(х-3); х2-2х+3х-6 > х2+2х-3х-6; х2+х-6 > х2-х-6; х2- х2+х+х > -6+6; 2х > 0; х > 0 Ответ: х > 0 2). Решение: 7(х+1)+10 > 11-7(2-х); 7х+7+10 > 11- 14 +7х; 7х+17 > -3+7х; 7х-7х > -3-17; 0х > -20 Последнее неравенство 0х > -20 является верным при любом значении х, т.к. его левая часть всегда равна 0 Ответ: любое число 3). Решение: Принимаем одну из сторон пенала за х. по условию задачи она должна быть больше 5 см, получаем неравенство х > 5. Другая сторона пенала больше первой в 3 раза, т.е. 3х > 15. периметр прямоугольного пенала равен 2(х+3х) > 2(5+15), при упрощении данного неравенства получаем 8х > 40, следовательно предположение, выдвинутое в задании верно. Ответ: предположение верно 3х х
Cлайд 11
* 1).Доказательство: (х+1)(х-6) > (х+7)(х-3); х2+х-6х-6 > х2+2х-3х-6; х2-5х-6 > х2-х-6; х2- х2+х-5х > -6+6; -4х > 0; х < 0. Ответ: х < 0 2). Решение: 5(1-х)-4 > 7-5х; 5-5х-4 > 7-5х; -5х +1 > 7-5х; -5х+5х>7-1; 0х > 6. Данное неравенство не имеет решений т.к. последнее неравенство 0х > 6 неверно. Ответ: решений нет 3).Решение . Сумма двух сторон треугольника должна быть больше третьей стороны. В данном случае третья сторона треугольника не должна быть длиннее суммы двух других его сторон. Обозначим длину неизвестной стороны за х. получим неравенство: х < 10+7 или х < 17. т.к. неравенство строгое число 17 не является решением неравенства. Значит наибольшая длина третьей стороны треугольника – 16 см Ответ: 16 сантиметров 10см 7см ?
Cлайд 12
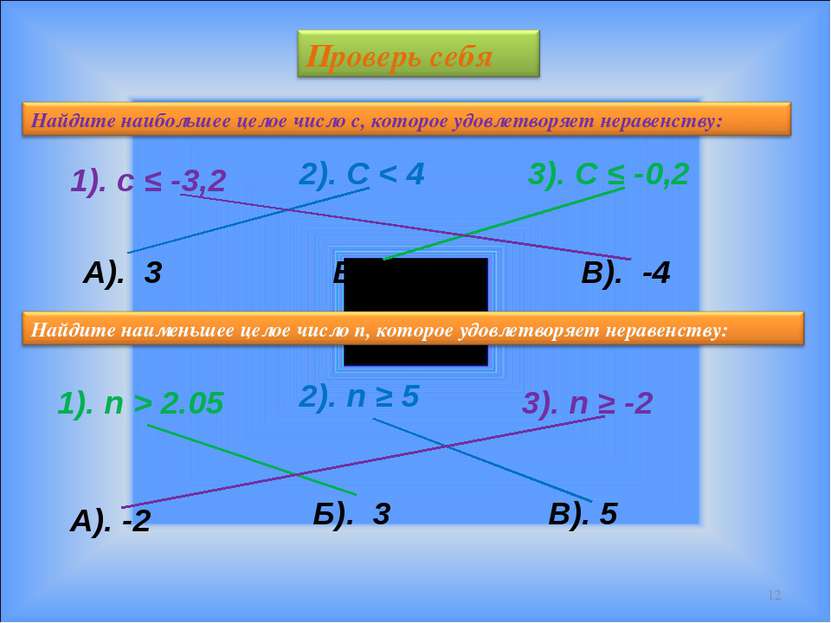
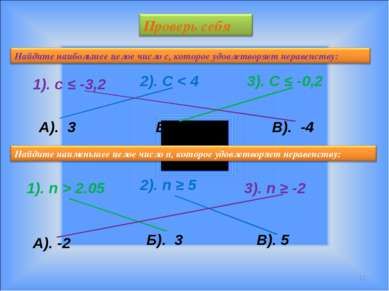* 1). с ≤ -3,2 2). С < 4 3). С ≤ -0,2 А). 3 В). -4 Б). -1 1). n > 2.05 2). n ≥ 5 3). n ≥ -2 А). -2 Б). 3 В). 5
Cлайд 13
* 1. При каких значениях z выражение принимает отрицательное значение: 2) 2. При каких значениях у сумма дробей и меньше значения дроби 3. При каких значениях a разность дробей и меньше или равна
Cлайд 14
*
