X
Код презентации скопируйте его
Многогранные углы
Скачать эту презентацию
Презентация на тему Многогранные углы
Скачать эту презентациюCлайд 1
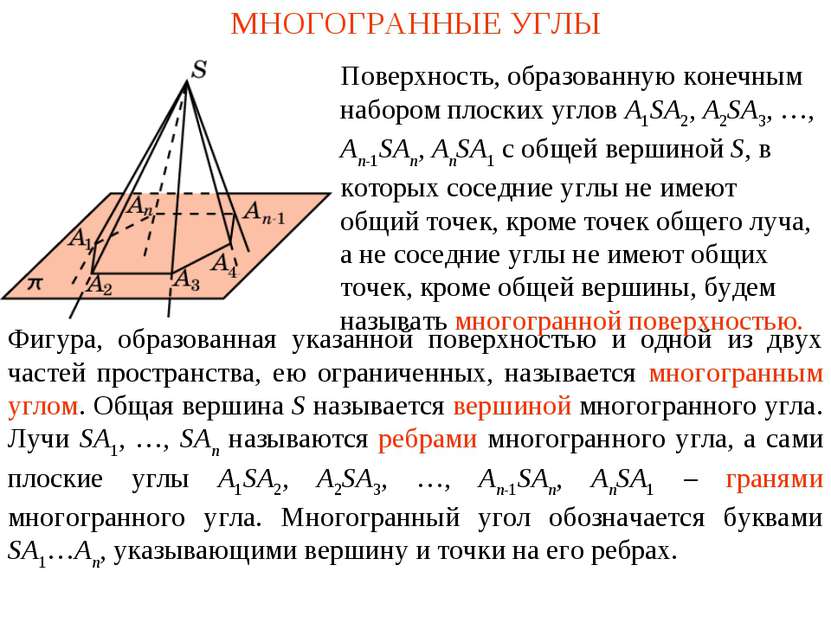
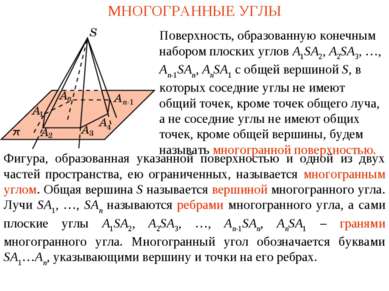МНОГОГРАННЫЕ УГЛЫ Фигура, образованная указанной поверхностью и одной из двух частей пространства, ею ограниченных, называется многогранным углом. Общая вершина S называется вершиной многогранного угла. Лучи SA1, …, SAn называются ребрами многогранного угла, а сами плоские углы A1SA2, A2SA3, …, An-1SAn, AnSA1 – гранями многогранного угла. Многогранный угол обозначается буквами SA1…An, указывающими вершину и точки на его ребрах. Поверхность, образованную конечным набором плоских углов A1SA2, A2SA3, …, An-1SAn, AnSA1 с общей вершиной S, в которых соседние углы не имеют общий точек, кроме точек общего луча, а не соседние углы не имеют общих точек, кроме общей вершины, будем называть многогранной поверхностью.
Cлайд 2
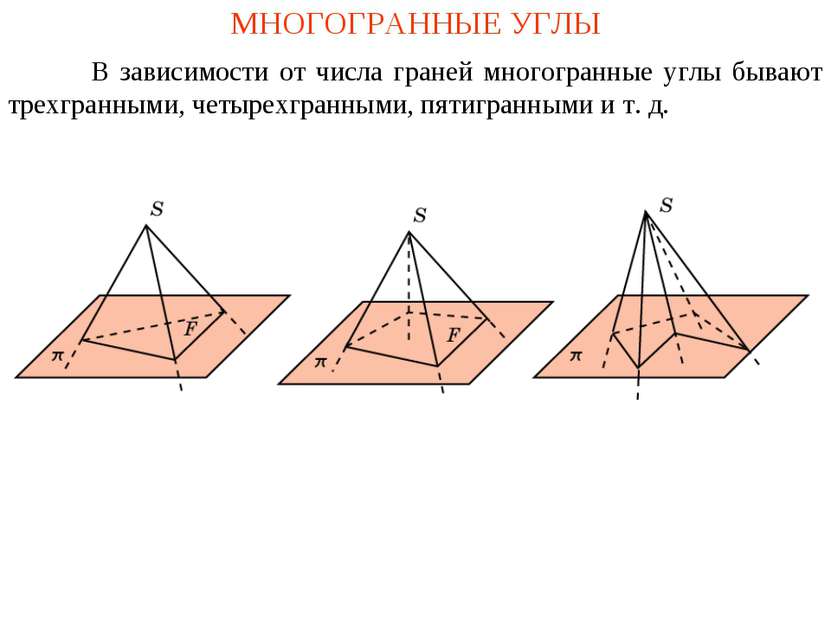
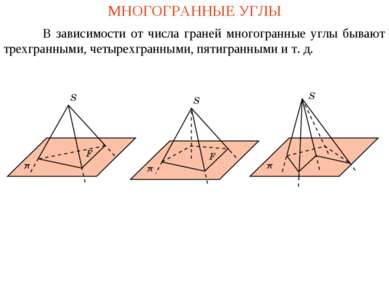МНОГОГРАННЫЕ УГЛЫ В зависимости от числа граней многогранные углы бывают трехгранными, четырехгранными, пятигранными и т. д.
Cлайд 3
ТРЕХГРАННЫЕ УГЛЫ Теорема. Всякий плоский угол трехгранного угла меньше суммы двух других его плоских углов. Доказательство. Рассмотрим трехгранный угол SABC. Пусть наибольший из его плоских углов есть угол ASC. Тогда выполняются неравенства ASB ASC
Cлайд 4
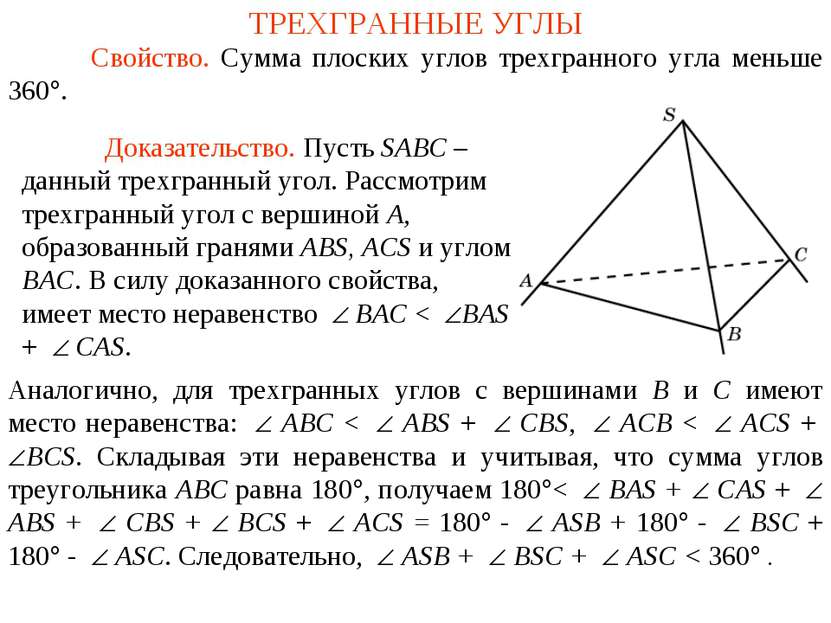
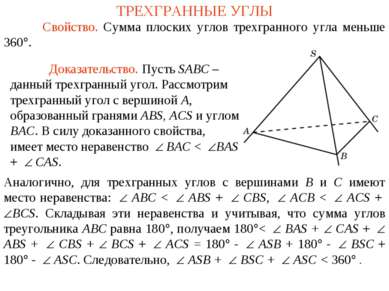ТРЕХГРАННЫЕ УГЛЫ Свойство. Сумма плоских углов трехгранного угла меньше 360°. Аналогично, для трехгранных углов с вершинами B и С имеют место неравенства: ABС
Cлайд 5
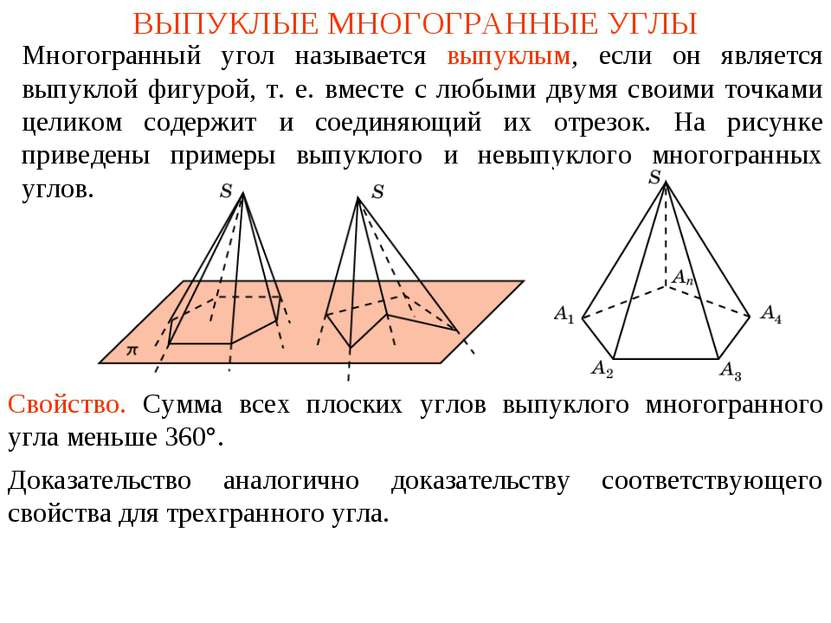
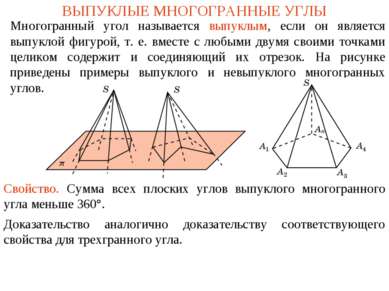ВЫПУКЛЫЕ МНОГОГРАННЫЕ УГЛЫ Многогранный угол называется выпуклым, если он является выпуклой фигурой, т. е. вместе с любыми двумя своими точками целиком содержит и соединяющий их отрезок. На рисунке приведены примеры выпуклого и невыпуклого многогранных углов. Свойство. Сумма всех плоских углов выпуклого многогранного угла меньше 360°. Доказательство аналогично доказательству соответствующего свойства для трехгранного угла.
Cлайд 6
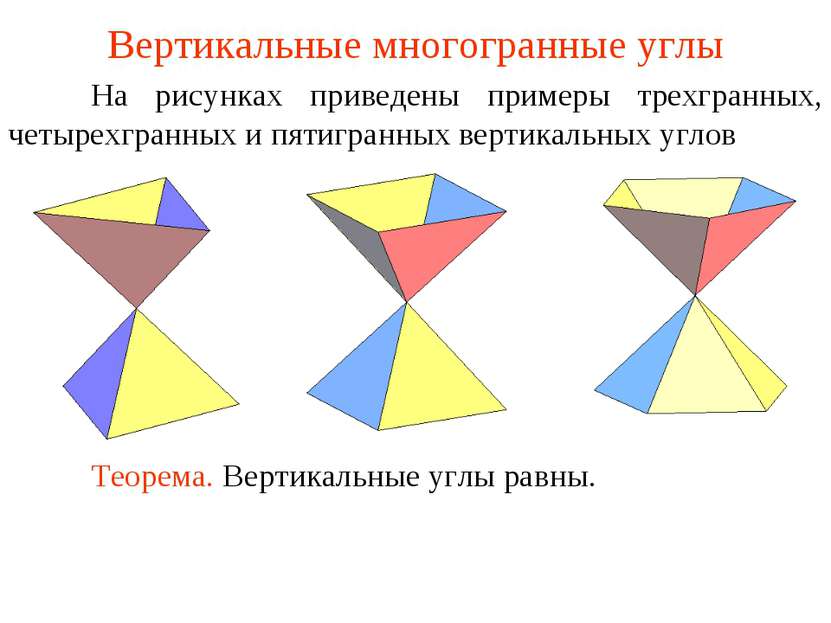
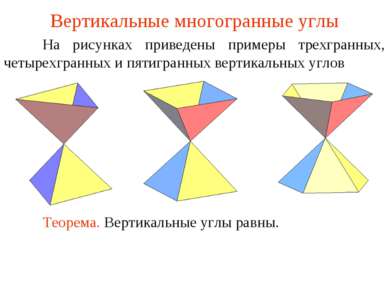Вертикальные многогранные углы На рисунках приведены примеры трехгранных, четырехгранных и пятигранных вертикальных углов Теорема. Вертикальные углы равны.
Cлайд 7
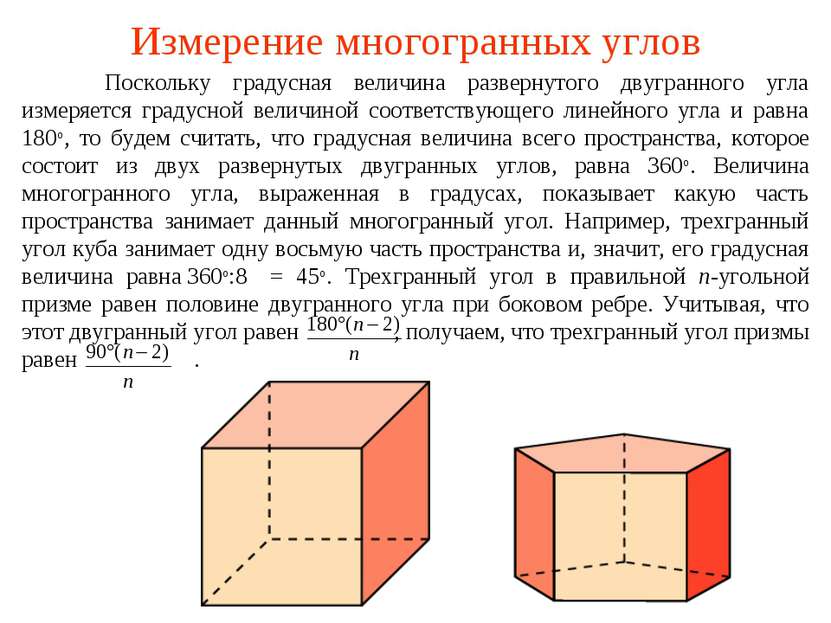
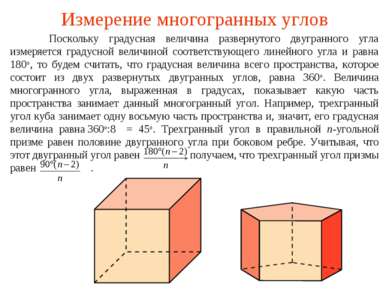Измерение многогранных углов Поскольку градусная величина развернутого двугранного угла измеряется градусной величиной соответствующего линейного угла и равна 180о, то будем считать, что градусная величина всего пространства, которое состоит из двух развернутых двугранных углов, равна 360о. Величина многогранного угла, выраженная в градусах, показывает какую часть пространства занимает данный многогранный угол. Например, трехгранный угол куба занимает одну восьмую часть пространства и, значит, его градусная величина равна 360о:8 = 45о. Трехгранный угол в правильной n-угольной призме равен половине двугранного угла при боковом ребре. Учитывая, что этот двугранный угол равен , получаем, что трехгранный угол призмы равен .
Cлайд 8
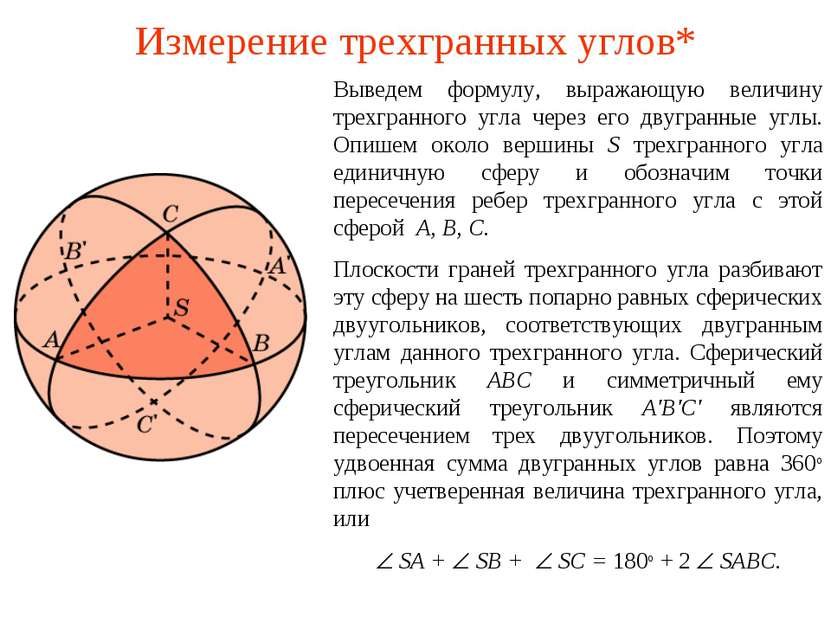
Измерение трехгранных углов* Выведем формулу, выражающую величину трехгранного угла через его двугранные углы. Опишем около вершины S трехгранного угла единичную сферу и обозначим точки пересечения ребер трехгранного угла с этой сферой A, B, C. Плоскости граней трехгранного угла разбивают эту сферу на шесть попарно равных сферических двуугольников, соответствующих двугранным углам данного трехгранного угла. Сферический треугольник ABC и симметричный ему сферический треугольник A'B'C' являются пересечением трех двуугольников. Поэтому удвоенная сумма двугранных углов равна 360о плюс учетверенная величина трехгранного угла, или SA + SB + SC = 180о + 2 SABC.
Cлайд 9
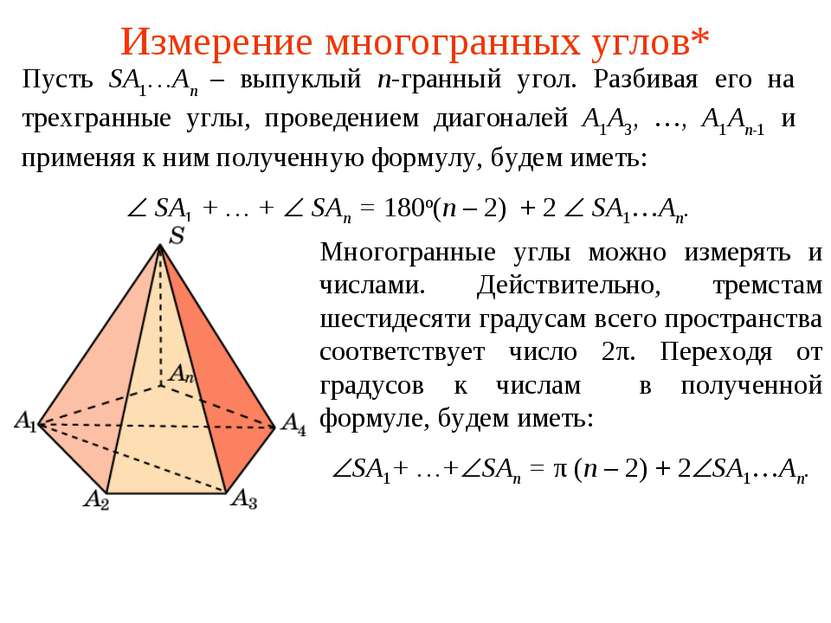
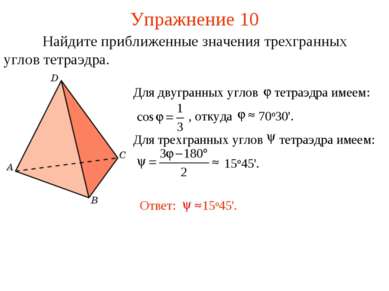
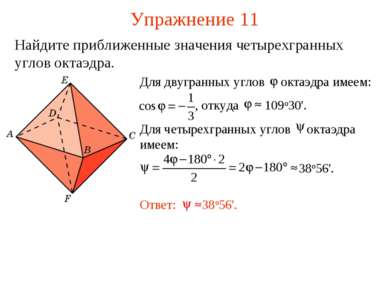
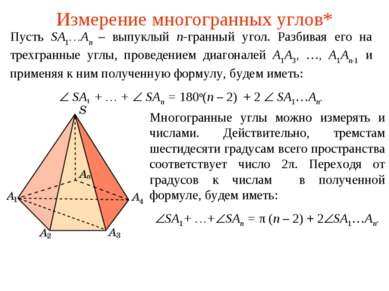Измерение многогранных углов* Пусть SA1…An – выпуклый n-гранный угол. Разбивая его на трехгранные углы, проведением диагоналей A1A3, …, A1An-1 и применяя к ним полученную формулу, будем иметь: SA1 + … + SAn = 180о(n – 2) + 2 SA1…An. Многогранные углы можно измерять и числами. Действительно, тремстам шестидесяти градусам всего пространства соответствует число 2π. Переходя от градусов к числам в полученной формуле, будем иметь: SA1+ …+ SAn = π (n – 2) + 2 SA1…An.
Cлайд 10
Упражнение 1 Может ли быть трехгранный угол с плоскими углами: а) 30°, 60°, 20°; б) 45°, 45°, 90°; в) 30°, 45°, 60°? Ответ: а) Нет; б) нет; в) да.
Cлайд 11
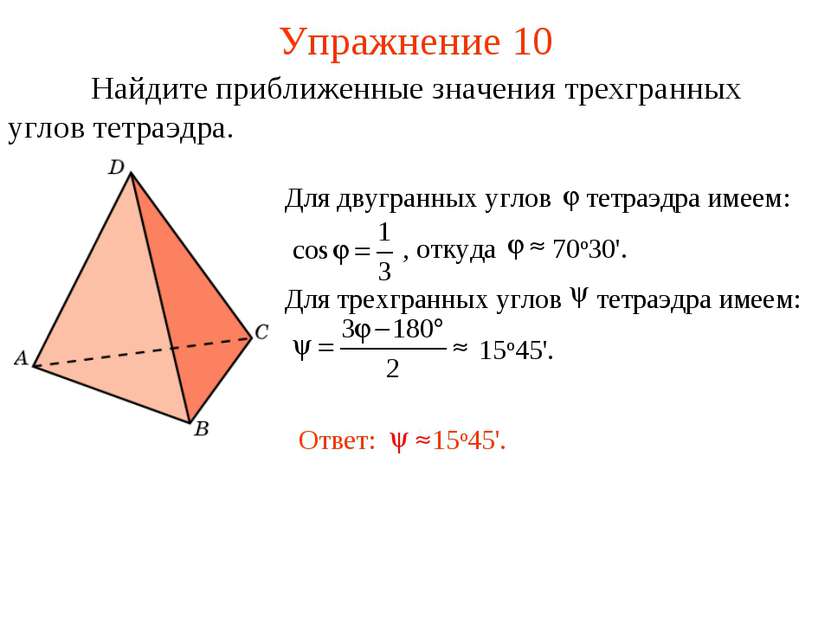
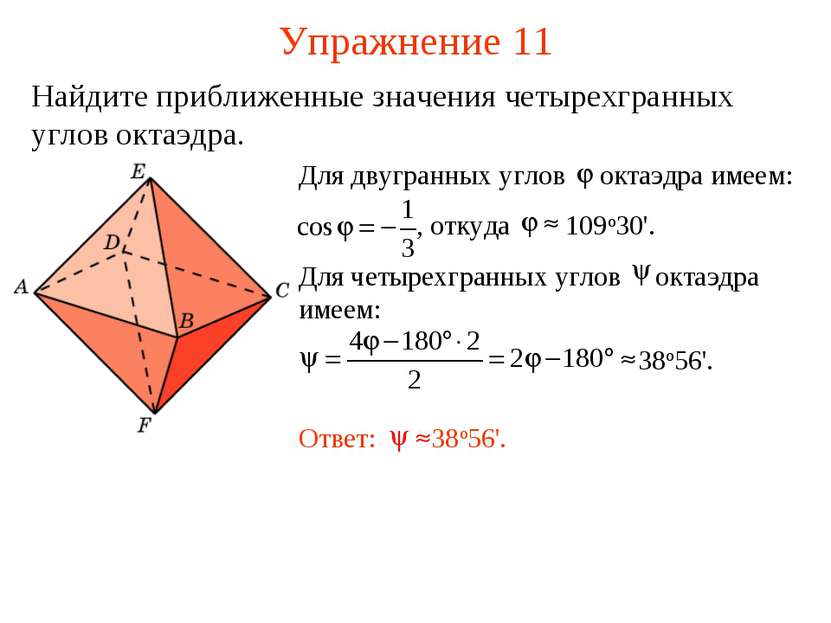
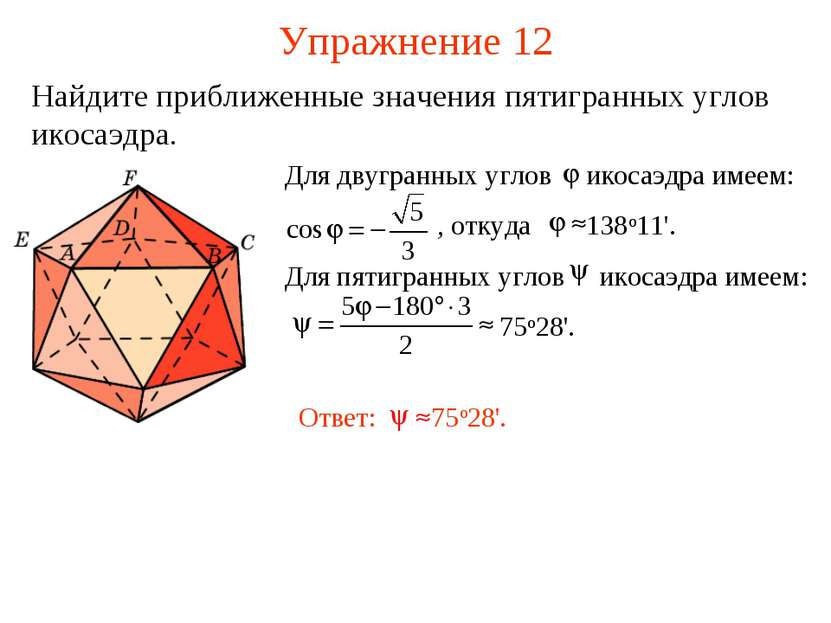
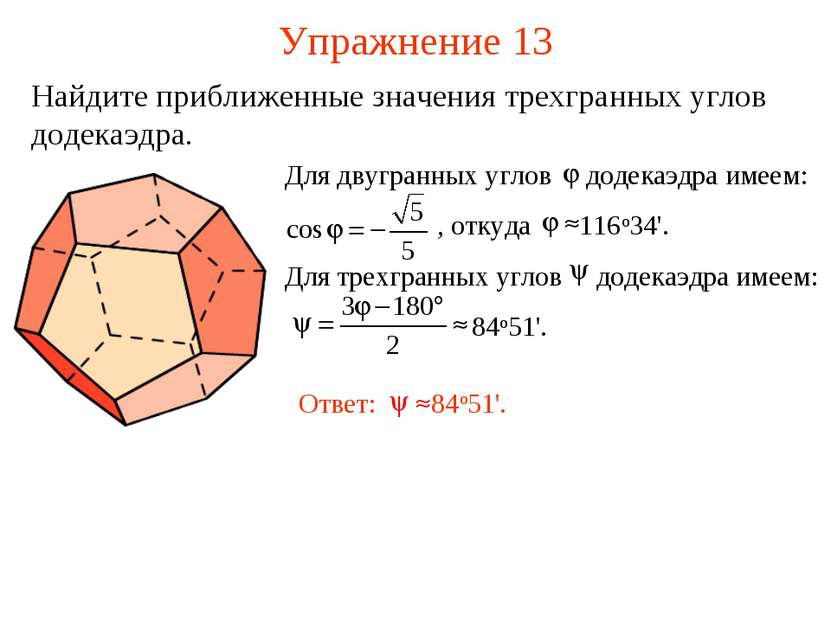
Упражнение 2 Приведите примеры многогранников, у которых грани, пересекаясь в вершинах, образуют только: а) трехгранные углы; б) четырехгранные углы; в) пятигранные углы. Ответ: а) Тетраэдр, куб, додекаэдр; б) октаэдр; в) икосаэдр.
Cлайд 12
Упражнение 3 Два плоских угла трехгранного угла равны 70° и 80°. В каких границах находится третий плоский угол? Ответ: 10о < < 150о.
Cлайд 13
Упражнение 4 Плоские углы трехгранного угла равны 45°, 45° и 60°. Найдите величину угла между плоскостями плоских углов в 45°. Ответ: 90о.
Cлайд 14
Упражнение 5 В трехгранном угле два плоских угла равны по 45°; двугранный угол между ними прямой. Найдите третий плоский угол. Ответ: 60о.
Cлайд 15
Упражнение 6 Плоские углы трехгранного угла равны 60°, 60° и 90°. На его ребрах от вершины отложены равные отрезки OA, OB, OC. Найдите двугранный угол между плоскостью угла в 90° и плоскостью ABC. Ответ: 90о.
Cлайд 16
Упражнение 7 Каждый плоский угол трехгранного угла равен 60°. На одном из его ребер отложен от вершины отрезок, равный 3 см, и из его конца опущен перпендикуляр на противоположную грань. Найдите длину этого перпендикуляра.
Cлайд 17
Упражнение 8 Найдите геометрическое место внутренних точек трехгранного угла, равноудаленных от его граней. Ответ: Луч, вершиной которого является вершина трехгранного угла, лежащий на линии пересечения плоскостей, делящих двугранные углы пополам.
Cлайд 18
Упражнение 9 Найдите геометрическое место внутренних точек трехгранного угла, равноудаленных от его ребер. Ответ: Луч, вершиной которого является вершина трехгранного угла, лежащий на линии пересечения плоскостей, проходящих через биссектрисы плоских углов и перпендикулярных плоскостям этих углов.
Cлайд 19
Упражнение 10 Найдите приближенные значения трехгранных углов тетраэдра.
Cлайд 20
Упражнение 11 Найдите приближенные значения четырехгранных углов октаэдра.
Cлайд 21
Упражнение 12 Найдите приближенные значения пятигранных углов икосаэдра.
Cлайд 22
Упражнение 13 Найдите приближенные значения трехгранных углов додекаэдра.
Cлайд 23
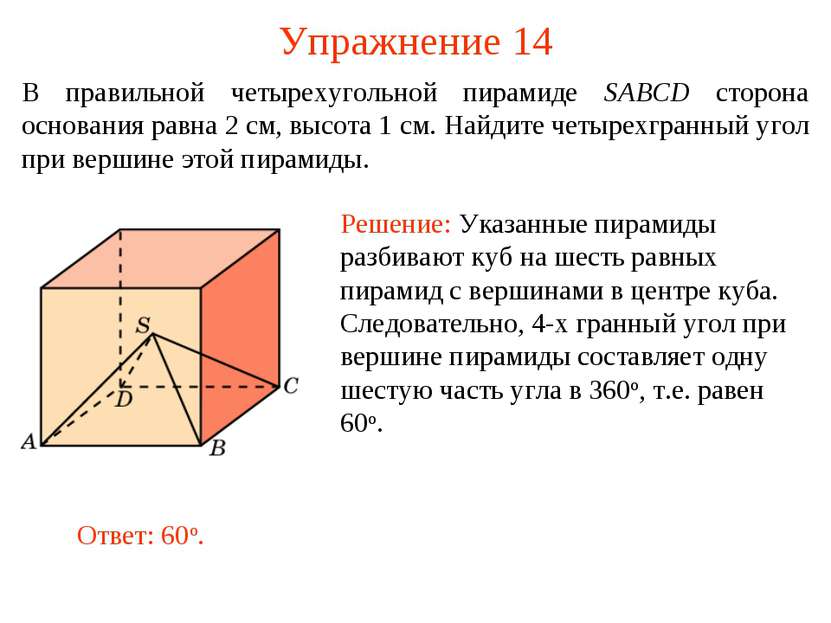
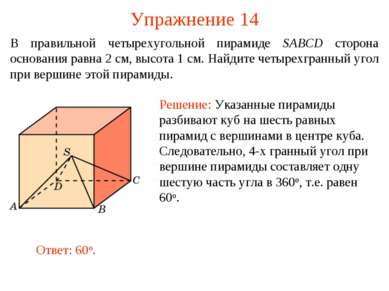Упражнение 14 В правильной четырехугольной пирамиде SABCD сторона основания равна 2 см, высота 1 см. Найдите четырехгранный угол при вершине этой пирамиды.
Cлайд 24
Упражнение 15 В правильной треугольной пирамиде боковые ребра равны 1, углы при вершине 90о. Найдите трехгранный угол при вершине этой пирамиды.
Cлайд 25
Упражнение 16 В правильной треугольной пирамиде боковые ребра равны 1, а высота Найдите трехгранный угол при вершине этой пирамиды.
