X
Код презентации скопируйте его
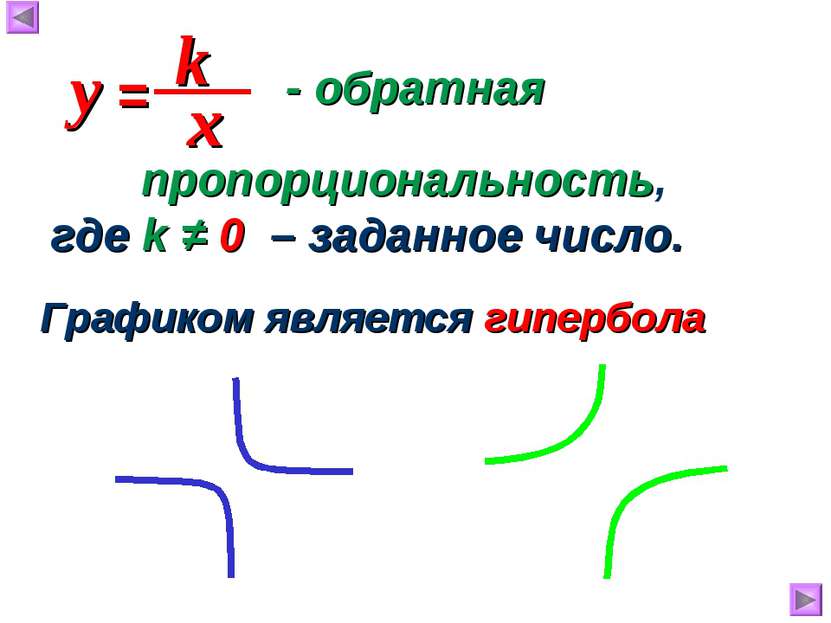
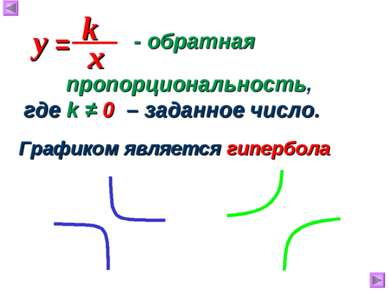
Функция у=к/х, её свойства и график
Скачать эту презентацию
Презентация на тему Функция у=к/х, её свойства и график
Скачать эту презентациюCлайд 1
Функция , её свойства и график. 8 класс учебник Мордковича А. Г. Ткаченко И. В. гимназия №5 г. Мурманск
Cлайд 2
Cлайд 3
Cлайд 4
- обратная Графиком является гипербола пропорциональность, где k ≠ 0 – заданное число.
Cлайд 5
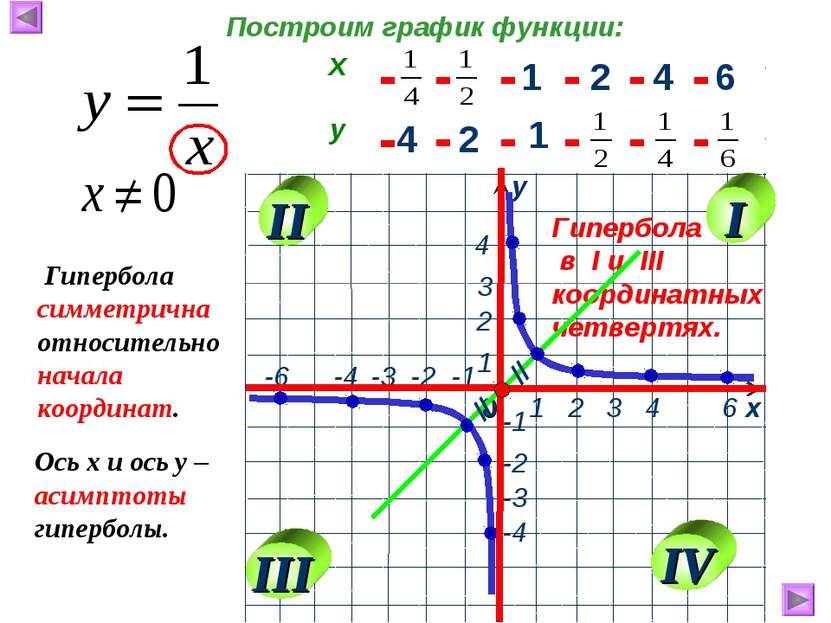
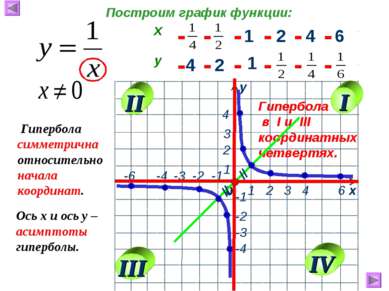1 2 4 6 4 2 1 - - - - - - - - - - - - Гипербола в I и III координатных четвертях. Построим график функции: Ось х и ось у – асимптоты гиперболы. // // Гипербола симметрична относительно начала координат. I II III IV х у
Cлайд 6
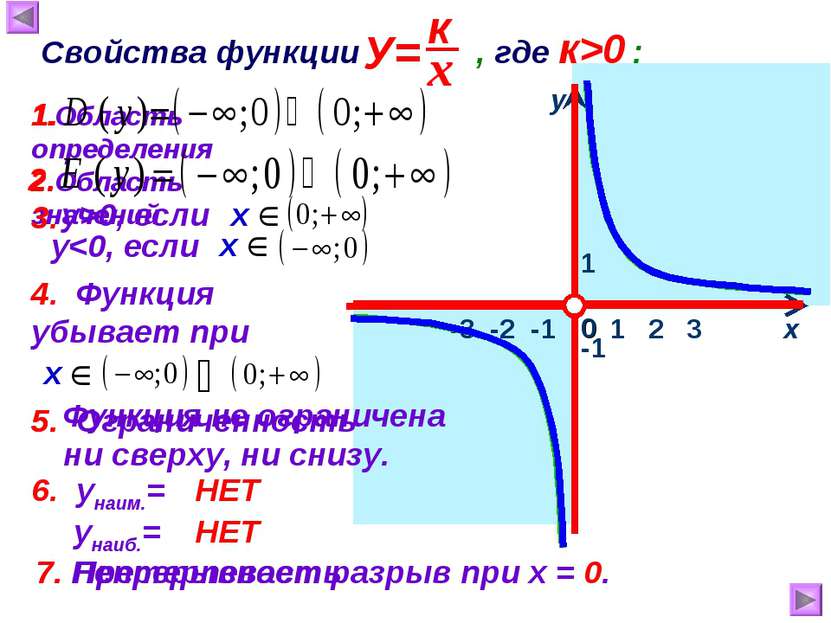
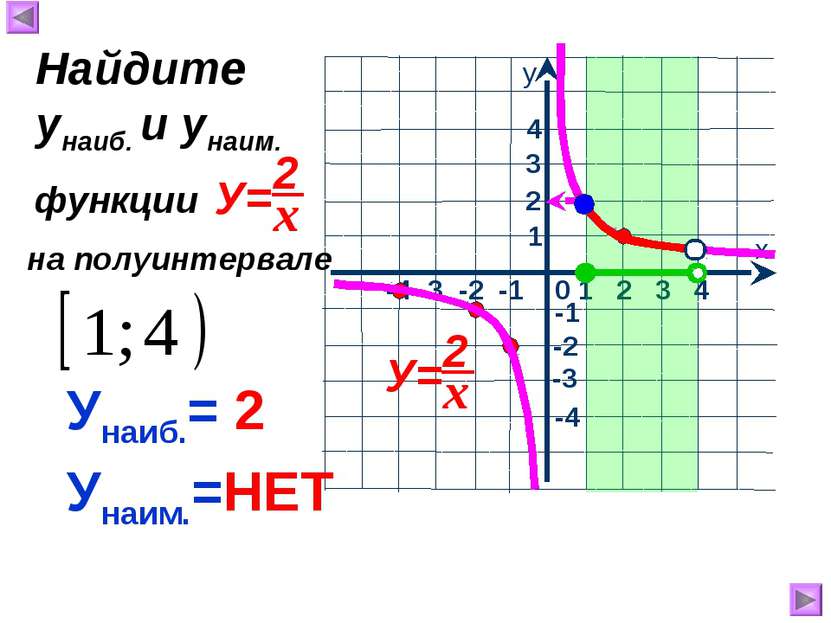
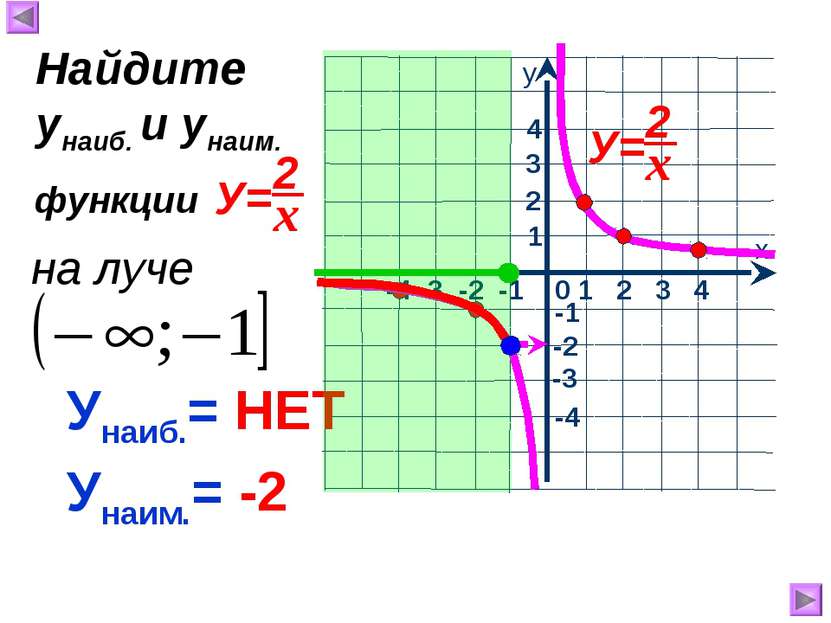
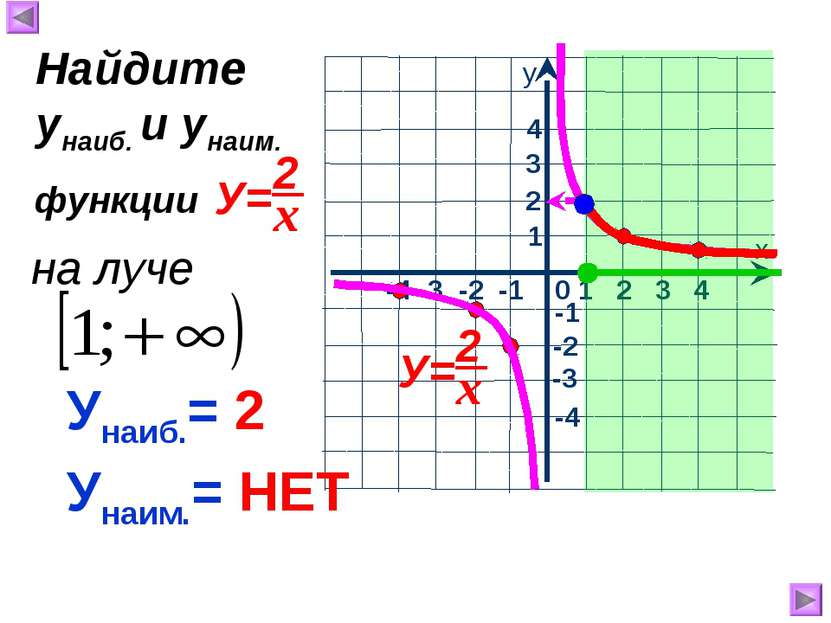
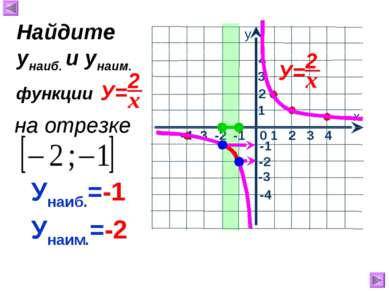
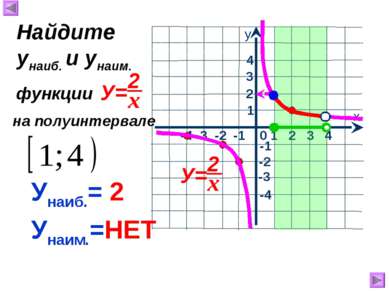
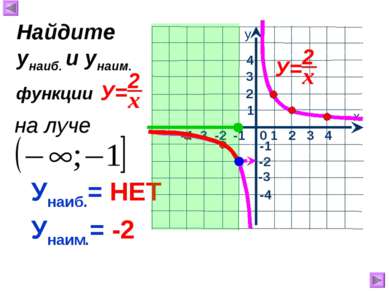
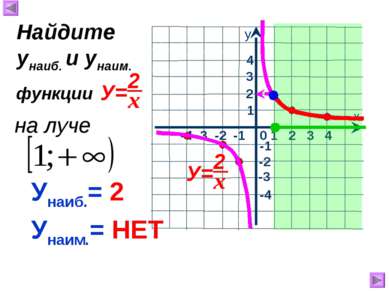
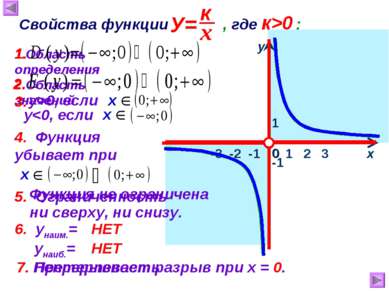1 х у 0 Свойства функции , где к>0 : 1.Область определения -1 2.Область значений 3. 1 2 3 у>0, если 4. Функция убывает при 5. Ограниченность 1. 2. 5. Функция не ограничена ни сверху, ни снизу. 6. унаим.= унаиб.= НЕТ НЕТ 7. Непрерывность 7. Претерпевает разрыв при х = 0. -3 -2 -1
Cлайд 7
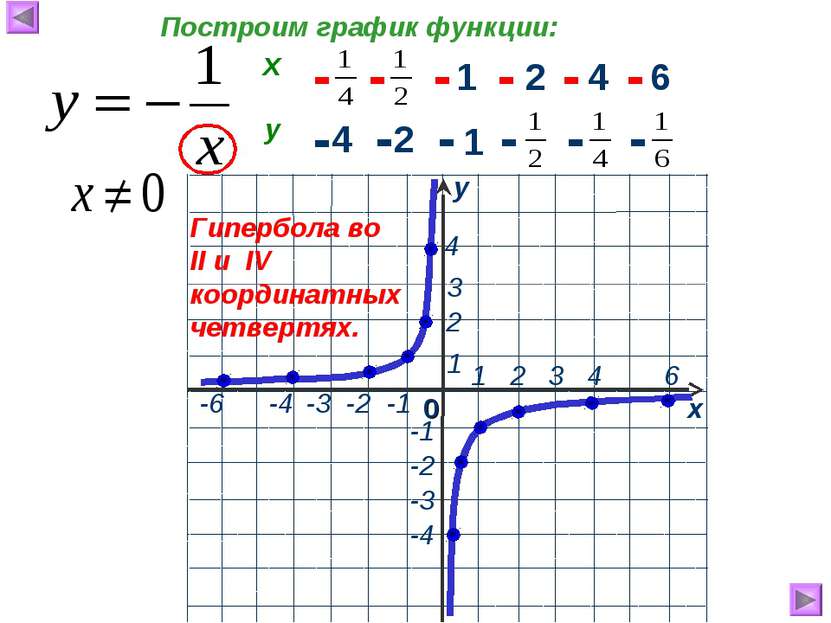
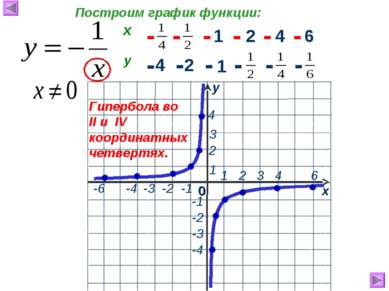1 2 4 6 4 2 1 - - - - - - - - - - - - Гипербола во II и IV координатных четвертях. Построим график функции: х у
Cлайд 8
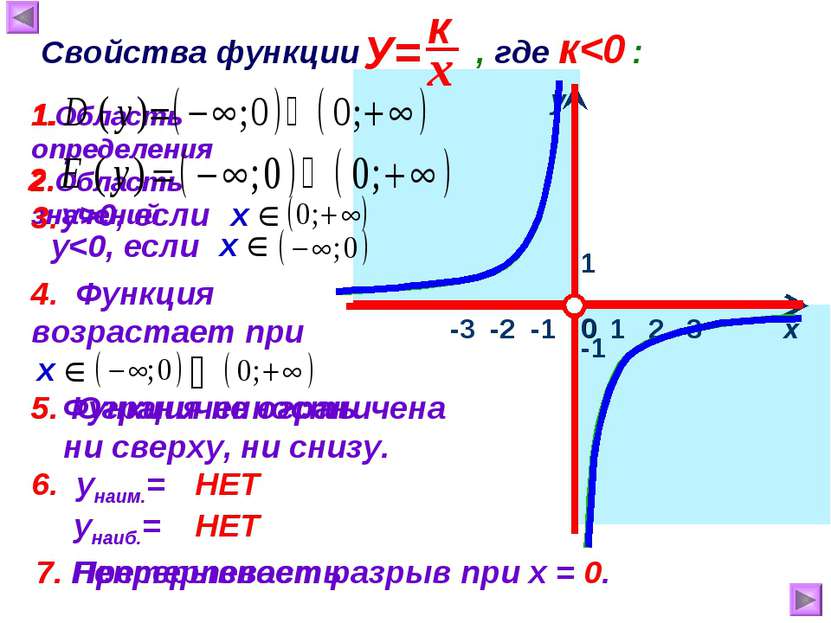
1 х у 0 Свойства функции , где к0, если 4. Функция возрастает при 5. Ограниченность 1. 2. 5. Функция не ограничена ни сверху, ни снизу. 6. унаим.= унаиб.= НЕТ НЕТ 7. Непрерывность 7. Претерпевает разрыв при х = 0. -3 -2 -1
Cлайд 9
Унаиб.=-1 Унаим.=-2 Найдите унаиб. и унаим. на отрезке функции
Cлайд 10
Унаиб.= 2 Унаим.=НЕТ Найдите унаиб. и унаим. на полуинтервале функции
Cлайд 11
Унаиб.= НЕТ Унаим.= -2 Найдите унаиб. и унаим. функции на луче
Cлайд 12
Унаиб.= 2 Унаим.= НЕТ Найдите унаиб. и унаим. функции на луче
Cлайд 13
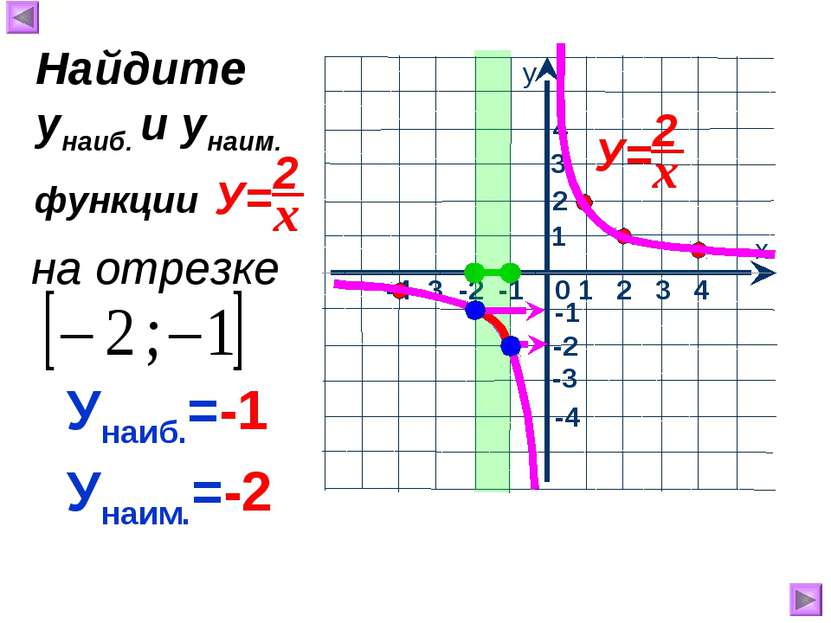
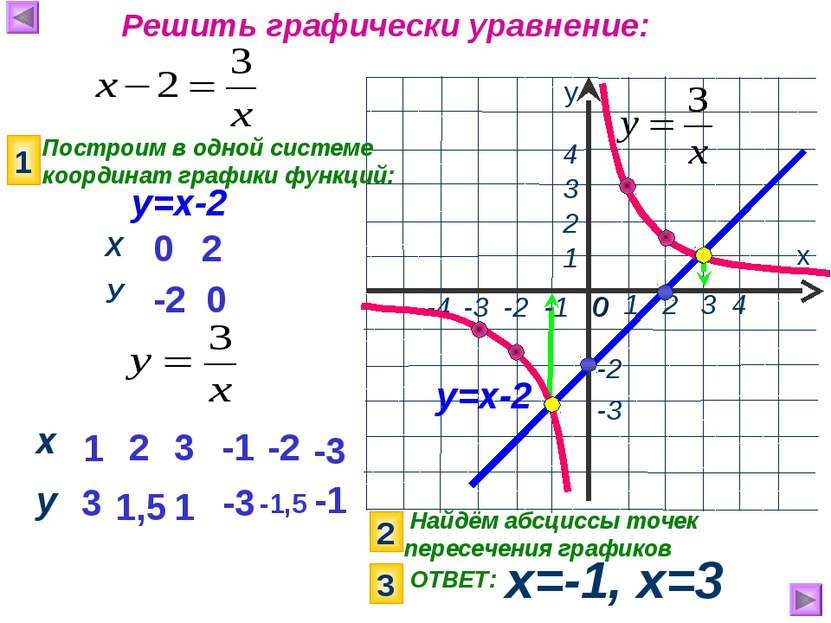
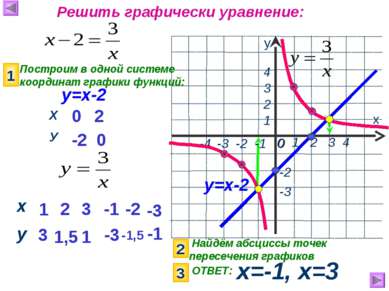Найдём абсциссы точек пересечения графиков х=-1, х=3 х у 1 2 3 4 0 -3 1 2 4 Решить графически уравнение: у=х-2 у=х-2 -4 -3 -2 -1 3 -2 Построим в одной системе координат графики функций: 1 0 -2 2 0 2 3 ОТВЕТ: 1 3 2 1,5 3 1 -1 -3 -2 -1,5 -3 -1 Х У х у
Cлайд 14
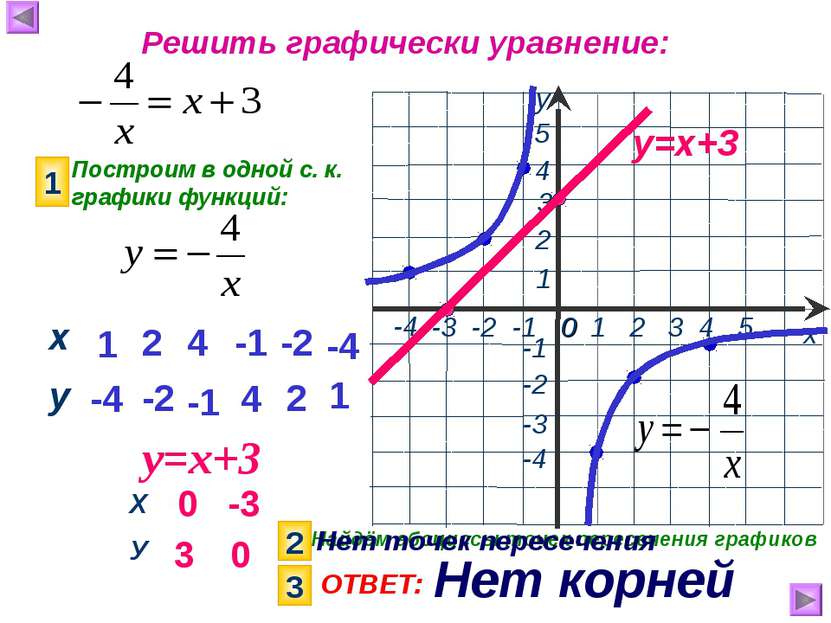
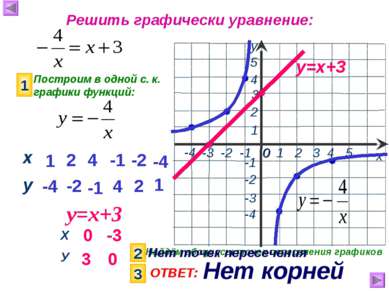Решить графически уравнение: Построим в одной с. к. графики функций: 1 у=х+3 1 -4 2 -2 4 -1 -1 4 -2 2 -4 1 0 3 -3 0 у=х+3 2 Найдём абсциссы точек пересечения графиков 3 ОТВЕТ: Нет корней Нет точек пересечения х у Х У
Cлайд 15
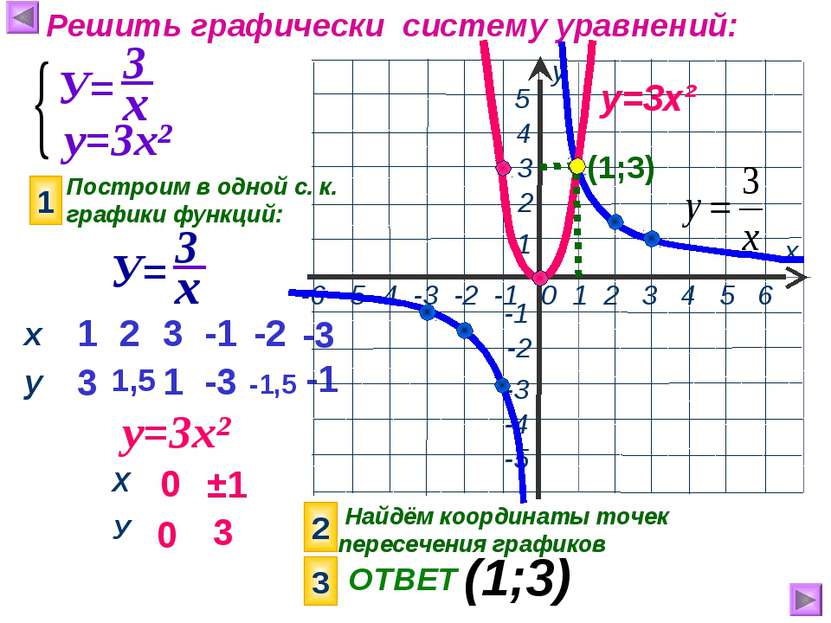
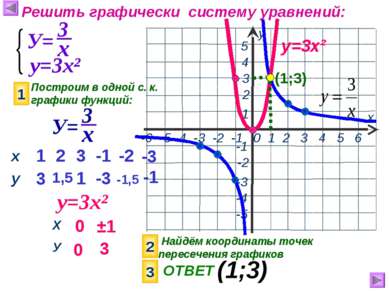Решить графически систему уравнений: у=3х² Построим в одной с. к. графики функций: 1 у=3х² 1 3 2 1,5 3 -1 1 -3 0 0 ±1 3 2 Найдём координаты точек пересечения графиков 3 ОТВЕТ (1;3) -2 -1,5 -3 -1 у=3х² (1;3) х у Х У
Cлайд 16
f(x)= -x²,если -2≤х≤1 ,если х>1 Постройте график функции и опишите её свойства.
Cлайд 17
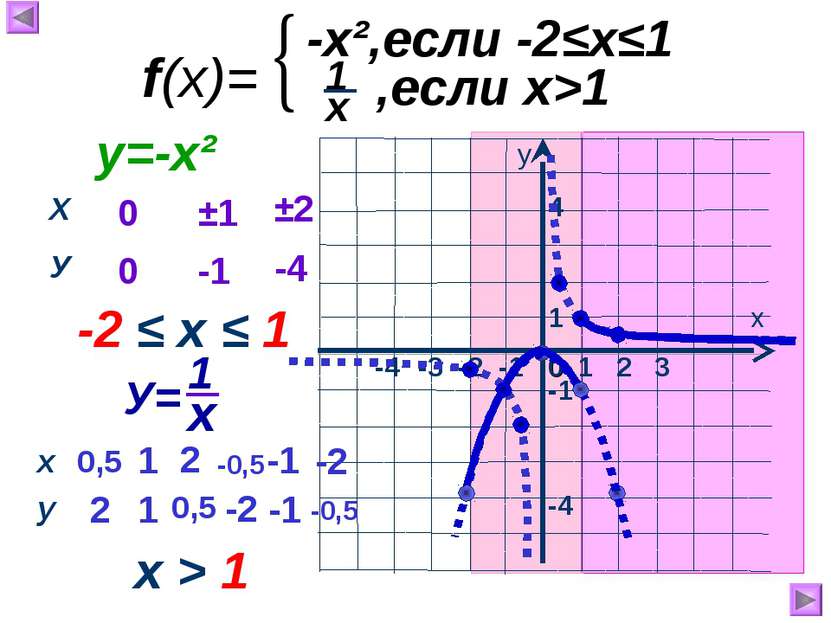
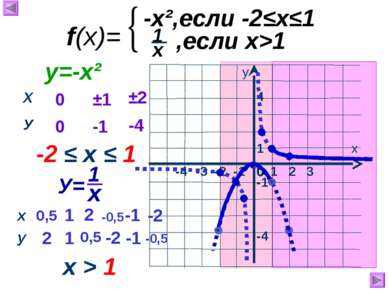1 х у 0 -3 -2 -1 -4 -1 -4 1 2 3 4 f(x)= -x²,если -2≤х≤1 ,если х>1 0 0 ±1 -1 ±2 -4 -2 ≤ х ≤ 1 у=-х² 1 1 2 0,5 -1 2 -2 -1 -0,5 -2 0,5 -0,5 х > 1 Х У х у
Cлайд 18
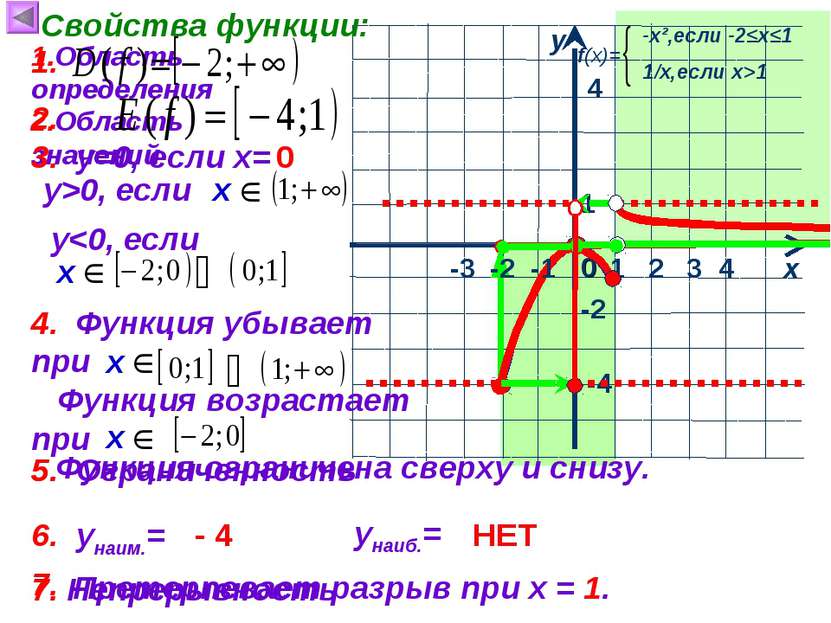
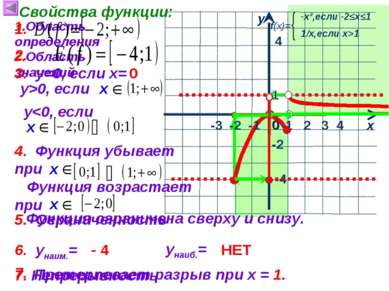1 х у 0 Свойства функции: 1.Область определения 4 4 -2 -4 2.Область значений 3. у=0, если х= 0 1 2 3 у>0, если 4. Функция убывает при Функция возрастает при 5. Ограниченность 1. 2. 5. Функция ограничена сверху и снизу. 6. унаим.= унаиб.= - 4 НЕТ 7. Непрерывность 7. Претерпевает разрыв при х = 1. -3 -2 -1
