Возрастание и убывание функции

Скачать эту презентацию

Получить код Увеличить

Возрастание и убывание функции. Рано или поздно всякая правильная математичес...

Числовые промежутки [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;...

Функция f(x) называется возрастающей на некотором промежутке, если большему з...

Функция f(x) называется убывающей на некотором промежутке, если большему знач...

Теорема Лагранжа Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцир...

y x A B касательная с A(α;f(α)) B(b;f(b)) y=f(x) угловой коэффициент секущей ...

Достаточные условия возрастания и убывания функции Пусть функция f(х) непреры...

доказательство: Пусть х1 и х2 - произвольные точки отрезка [α;b] , такие, что...

1 8

Презентация на тему Возрастание и убывание функции

Скачать эту презентацию

Cлайд 1

Возрастание и убывание функции. Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. А.Н. Крылов

Cлайд 2

Числовые промежутки [α;b] – отрезок (α;b) – интервал (α;b] – полуинтервал [α;b) - полуинтервал

Cлайд 3

Функция f(x) называется возрастающей на некотором промежутке, если большему значению аргумента соответствует большее значение функции. x1 > x2 f(x1 ) > f(x2)

Cлайд 4

Функция f(x) называется убывающей на некотором промежутке, если большему значению аргумента соответствует меньшее значение функции. x1 > x2 f(x1 ) < f(x2)

Cлайд 5

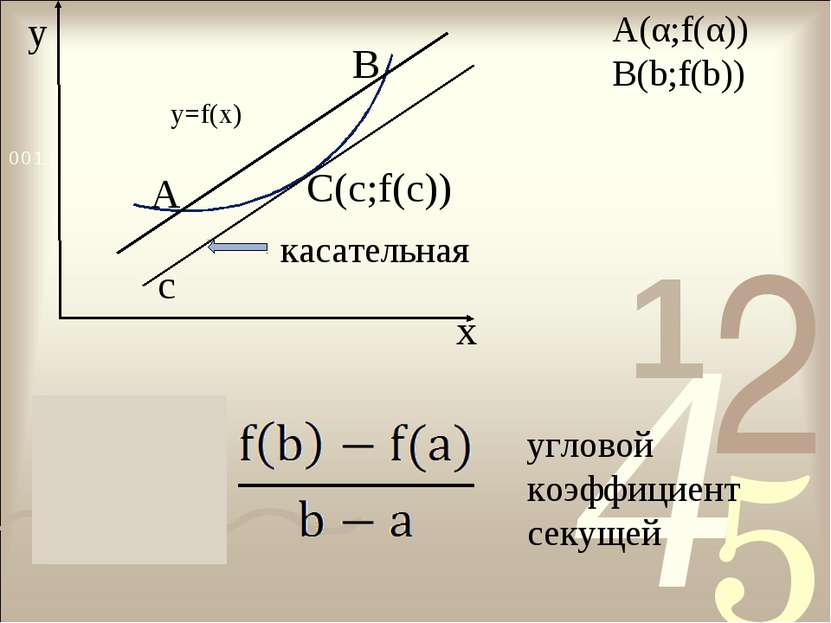
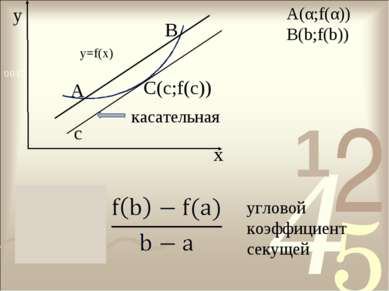
Теорема Лагранжа Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда существует точка с € (α;b), такая, что f(b) – f(α) = f ′(c) (b - α)

Cлайд 6

y x A B касательная с A(α;f(α)) B(b;f(b)) y=f(x) угловой коэффициент секущей C(c;f(с))

Cлайд 7

Достаточные условия возрастания и убывания функции Пусть функция f(х) непрерывна на отрезке [α;b] и дифференцируема на интервале (α;b). Тогда если f′(x)>0 для всех х € (α;b) , то функция f(x) возрастает на отрезке [α;b] , а если f′(x)

Cлайд 8

доказательство: Пусть х1 и х2 - произвольные точки отрезка [α;b] , такие, что х1 < х2 , т.е. х2- х1 >0 По теореме Лагранжа При f′(x)>0 f(х2) – f(х1) > 0 функция возрастает. При f′(x)