X
Код презентации скопируйте его
Применение свойств функций к решению уравнений и неравенств
Скачать эту презентацию
Презентация на тему Применение свойств функций к решению уравнений и неравенств
Скачать эту презентациюCлайд 1
Применим для задач в которых множества значений левой и правой частей уравнения или неравенства имеют единственную общую точку, являющуюся наибольшим значением для одной части и наименьшим для другой. Эту ситуацию хорошо иллюстрирует график. Как начинать решать такие задачи? МЕТОД МАЖОРАНТ Привести уравнение или неравенство к виду Сделать оценку обеих частей. Если существует число М, из области значений такое что , то Решить систему уравнений:
Cлайд 2
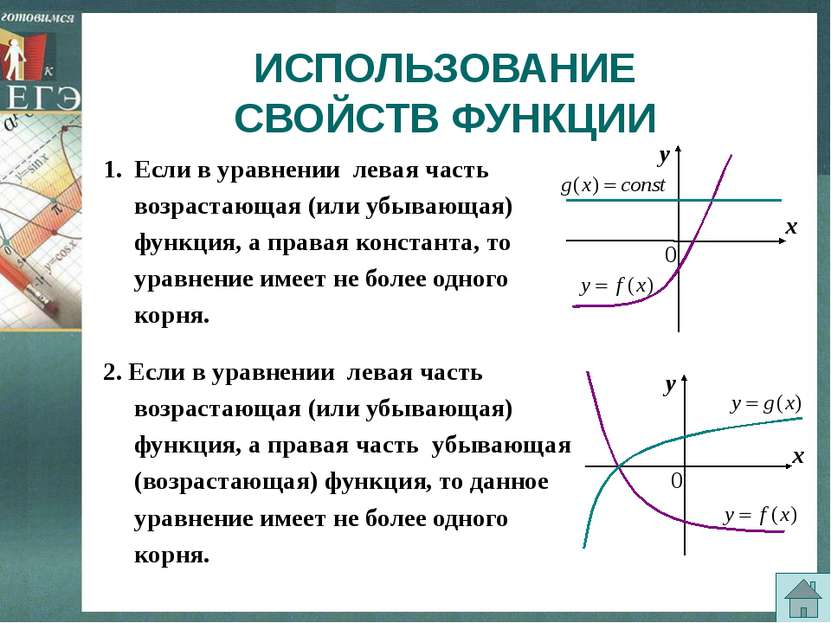
ИСПОЛЬЗОВАНИЕ СВОЙСТВ ФУНКЦИИ Если в уравнении левая часть возрастающая (или убывающая) функция, а правая константа, то уравнение имеет не более одного корня. 2. Если в уравнении левая часть возрастающая (или убывающая) функция, а правая часть убывающая (возрастающая) функция, то данное уравнение имеет не более одного корня. х у 0 х у 0
Cлайд 3
Пример 9. Решить уравнение Решение: Заметим, что х = 1 , является корнем данного уравнения. Левая часть уравнения представляет собой сумму двух возрастающих функций и, следовательно, сама является возрастающей функцией, принимающей каждое своё значение ровно один раз. Поэтому других корней данное уравнение не имеет. Ответ: 1.
Cлайд 4
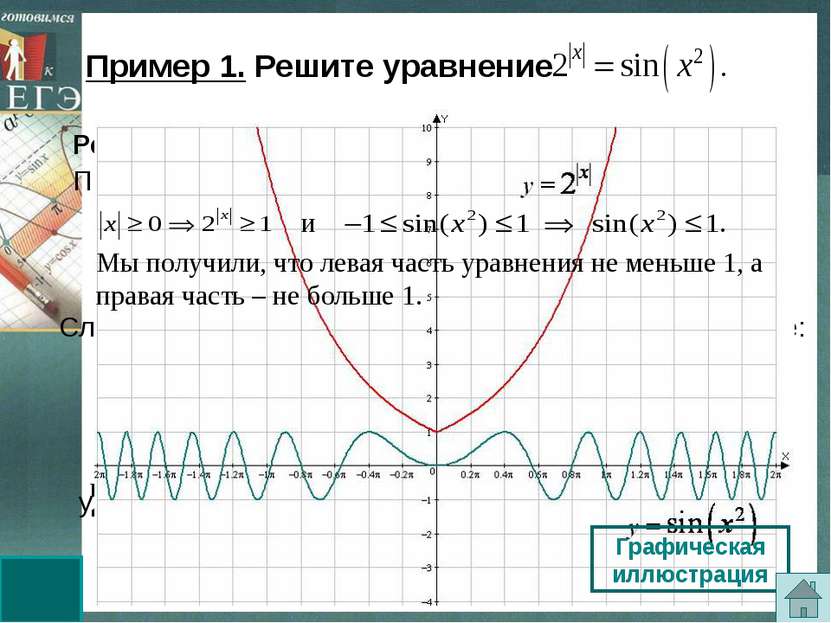
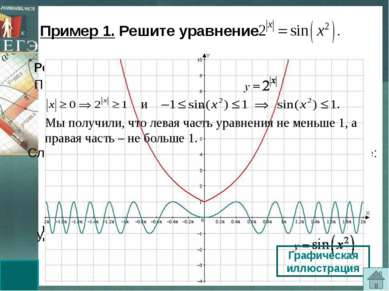удовлетворяет второму уравнению. Решение. Оценим обе части уравнения. При всех значениях х верны неравенства: Следовательно, данное уравнение равносильно системе: Графическая иллюстрация Мы получили, что левая часть уравнения не меньше 1, а правая часть – не больше 1. Ответ: . Пример 1. Решите уравнение Последняя система не имеет решений, так как не и
Cлайд 5
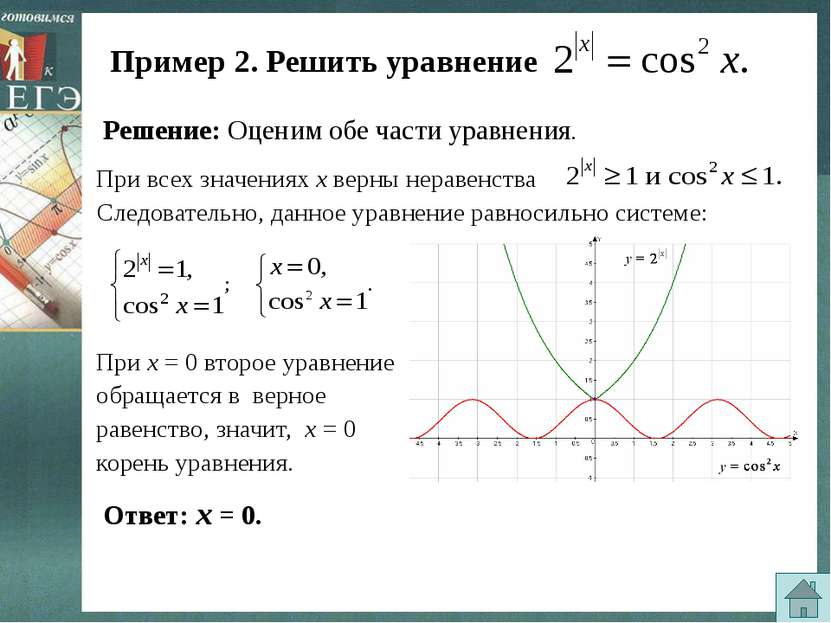
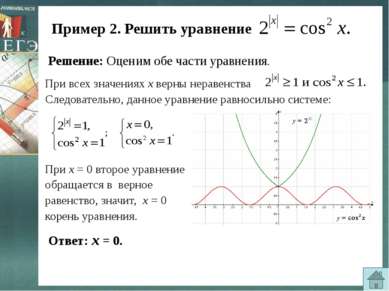Пример 2. Решить уравнение Решение: Оценим обе части уравнения. Следовательно, данное уравнение равносильно системе: При х = 0 второе уравнение обращается в верное равенство, значит, х = 0 корень уравнения. Ответ: х = 0. При всех значениях х верны неравенства
Cлайд 6
Сделаем оценку функций, входящих в неравенство. Пример 3. Решить неравенство Следовательно, исходное неравенство выполняется тогда и только тогда, когда оба множителя равны 1 одновременно. Ответ: - 1. Решение. Получаем х = -1 – единственное решение системы уравнений, а, значит, и данного неравенства. Очевидно что Так как , то данная функция принимает наибольшее значение равное 1 при х = -1, значит,
Cлайд 7
(так как: ). Пример 4. Решить уравнение Для правой части (в силу неравенства для суммы двух взаимно обратных чисел) выполнено Поэтому уравнение имеет решения, если и только если одновременно выполнены два условия принимает значение от 0,5 до 2 Решение. Оценим обе части уравнения. Так как то левая часть уравнения Решая последнюю систему, получаем Ответ:
Cлайд 8
Пример 5. Решить уравнение 2) Решая первое уравнение системы, находим : 3) Подставим найденные значения во второе уравнение: Решение. Оценим обе части уравнения. 1) Каждое слагаемое левой части уравнения не больше 1, следовательно их сумма будет равна 2, если они принимают своё наибольшее значение. Значит, уравнение равносильно системе: Следовательно, решение системы. Ответ:
Cлайд 9
Пример 6. Решить уравнение Решение. Оценим множители левой части уравнения. почленно эти неравенства, получаем: Следовательно, левая часть равна правой, лишь при условии: Значит, данное уравнение равносильно системе уравнений: Решая систему уравнений, получаем решения исходного уравнения: . Заметим, что перемножив Ответ: ? сумма двух положительных взаимообратных чисел ? ? сумма единицы и неотрицательного числа sin 3z [-1;1] 3 + sin3z [2; 4].
Cлайд 10
Содержание Метод мажорант (метод оценки) Использование свойств функций: Область определения Множество значений Четность и нечетность 3. Задачи с параметром 4. Задачи из сборника ЕГЭ, часть «С» 5. Использованные источники
Cлайд 11
Пример 10. Доказать, что уравнение не имеет решений: Арифметический корень не может быть отрицательным числом, поэтому уравнение решений не имеет. ? ? ? ? ? Находим ОДЗ уравнения: Не существует такого значения х, при котором оба выражения имеют смысл. Поэтому уравнение решений не имеет. Заметим,
Cлайд 12
ИСПОЛЬЗОВАНИЕ ОБЛАСТИ ОПРЕДЕЛЕНИЯ ФУНКЦИИ Итак, единственной точкой, в которой определены эти радикалы, является x = 1. Легко проверить, что это число – корень уравнения. Решить уравнение: Решение. Второй радикал определен при любых значениях х. Выражение под третьим радикалом неотрицательно если Ответ: 1. Первый радикал определен при х -3 -1 1
Cлайд 13
Решить уравнение 1) Выпишем, условие существования функции, стоящей в левой части: Решить данное неравенство довольно сложно. 3) Значит, исходное уравнение тоже не имеет решений, так как левая часть его – неотрицательная функция! Ответ: . Решение. 2) Проверим не отрицательность правой части: Последнее неравенство решений не имеет.
Cлайд 14
а = 1 а = 2 а = 3 а = -3 а = -2 а = -1 у = 1
Cлайд 15
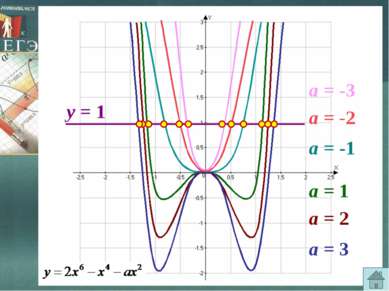
Может ли при каком-нибудь значении параметра а, уравнение Так как при замене х на –х данное уравнение не изменится, то множество его корней вместе с каждым корнем содержит противоположный корень. Следовательно, уравнение имеет четное число корней, отличных от нуля. Проверка показывает, что 0 – корень, значит, данное уравнение имеет нечетное число корней. иметь нечетное число корней? Решение. Ответ: да. ИСПОЛЬЗОВАНИЕ ЧЕТНОСТИ ФУНКЦИИ
Cлайд 16
Cлайд 17
Cлайд 18
Cлайд 19
Cлайд 20
Cлайд 21
