X
Код презентации скопируйте его
Построение графика функции методом ее исследования с помощью производной
Скачать эту презентацию
![Правильный ответ [-1;2] и [5;6)](https://bigslide.ru/images/32/31084/831/img29.jpg "Правильный ответ [-1;2] и [5;6)")
![Правильный ответ (-5;-1] и [2;5]](https://bigslide.ru/images/32/31084/831/img31.jpg "Правильный ответ (-5;-1] и [2;5]")
Презентация на тему Построение графика функции методом ее исследования с помощью производной
Скачать эту презентациюCлайд 1
НИПКиПРО КАФЕДРА МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ Проект урока по теме: «Построение графика функции методом ее исследования с помощью производной» г. Новосибирск 2008
Cлайд 2
доцент кафедры математического образования Батан Любовь Федоровна учитель математики первой квалификационной категории МОУ лицей № 176 Ткаченко Зоя Васильевна Автор: Научный руководитель:
Cлайд 3
Аннотация Урок алгебры рекомендован для учащихся 10 класса, обучающихся по учебнику «Алгебра и математический анализ» для углубленного изучения математики в общеобразовательных учреждениях авторов Н. Я. Виленкин, О. С. Ивашев-Мусатов, С. И. Шварцбурд. Программа соответствует обязательному минимуму среднего (полного) общего образования. Приказ №56 от 30. 06. 1999г. Издательство МНЕМОЗИНА Москва 2005
Cлайд 4
Актуальность Данная тема является очень важной и значимой, т. к. в материалах ЕГЭ большое внимание уделяется заданиям, связанным с исследованием функции с помощью графика, с построением графика заданной функции. Успешное изучение этой темы поможет вам хорошо сдать государственный экзамен по математике.
Cлайд 5
Тип урока Урок закрепления изученного материала в форме самостоятельной групповой работы по карточкам Оборудование: Smart-доска; Сканер; Персональный компьютер; Карточка с заданием на каждой парте.
Cлайд 6
Цели урока Для учителя Для ученика
Cлайд 7
Цели урока Обобщить и закрепить свои знания и умения при построении графика функции с помощью ее исследования. Применить (ИКТ) новые информационные технологии для проверки результатов построения с помощью программы MathCAD Воспитывать такие качества личности, как познавательная активность, самостоятельность, упорство в достижении цели
Cлайд 8
Цели урока Систематизировать, обобщить и расширить знания и умения учащихся при построении графиков функций. Развивать умения наблюдать, сравнивать, обобщать и анализировать математические ситуации с использованием ИКТ и программы MathCAD. Воспитывать такие качества личности, как познавательная активность, самостоятельность, упорство в достижении цели, коммуникативную и информационную культуру. Побуждать учеников к самоконтролю, взаимоконтролю и самоанализу своей деятельности.
Cлайд 9
Задачи урока Формировать устойчивый интерес к математике через дифференцированный подход к учащимся. Вовлекать каждого ученика в процесс активного учения через интерактивные методы обучения. Развивать познавательный интерес, графическую культуру, культуру речи, память, самостоятельность мышления.
Cлайд 10
Содержание урока Вводная беседа. Устная работа. Самостоятельная работа в группах. Обобщение. Итог. Историческая справка. Рефлексия.
Cлайд 11
На уроке мы должны закрепить и обобщить свои знания и умения при построении графика функции с помощью производной и убедиться в правильности своего построения с помощью программы MathCAD. Вводная беседа
Cлайд 12
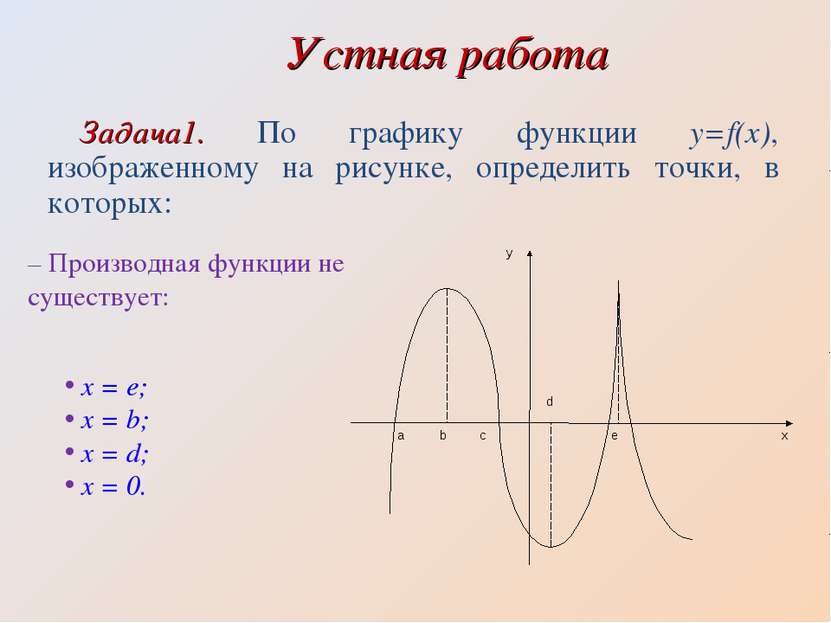
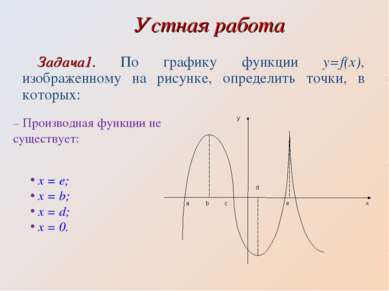Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить точки, в которых: – Производная функции не существует: x = e; x = b; x = d; x = 0.
Cлайд 13
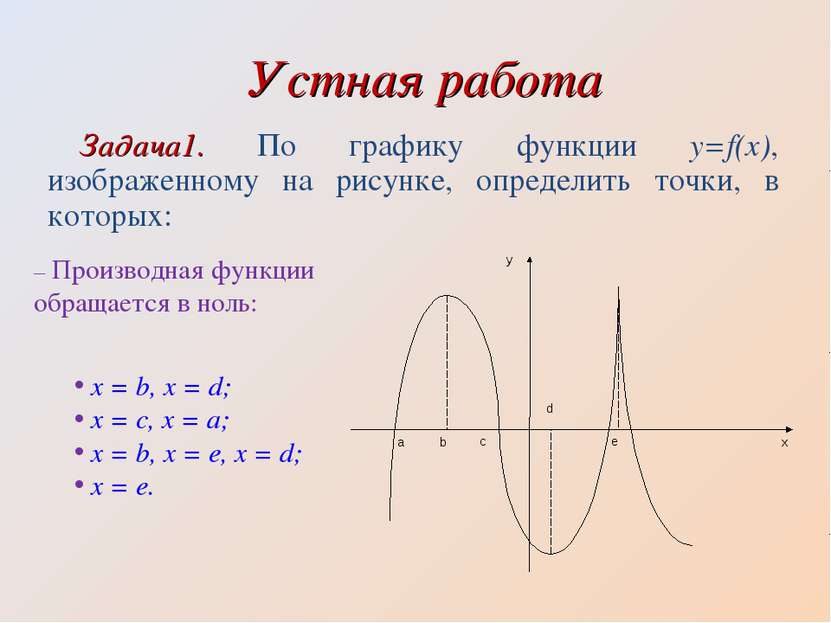
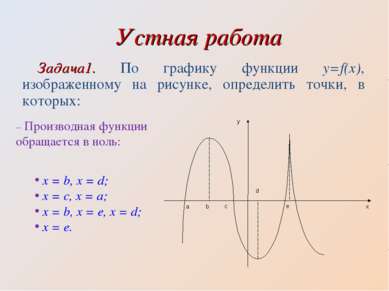Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить точки, в которых: – Производная функции обращается в ноль: x = b, x = d; x = c, x = a; x = b, x = e, x = d; x = e.
Cлайд 14
Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить: – Точки максимума функции: x = e; x = b; x = b, x = e; нет точек максимума.
Cлайд 15
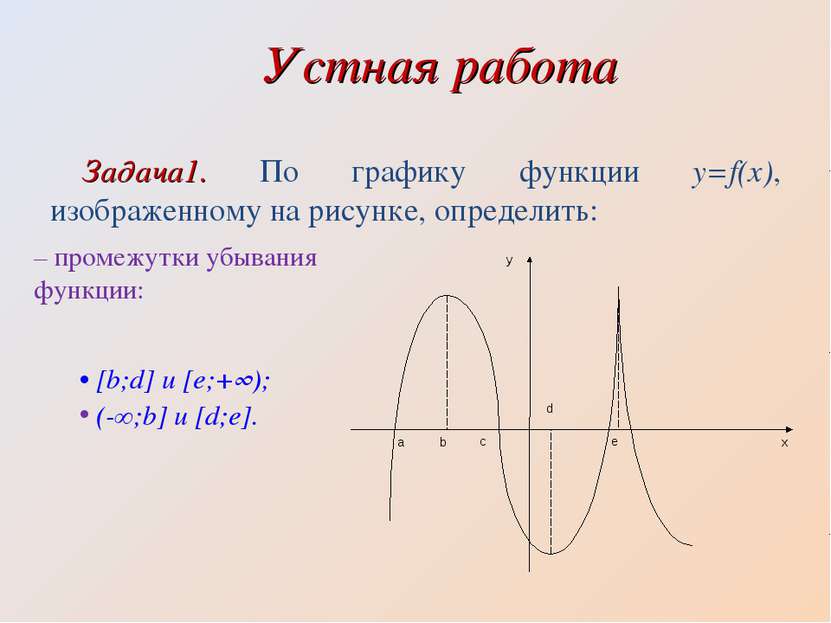
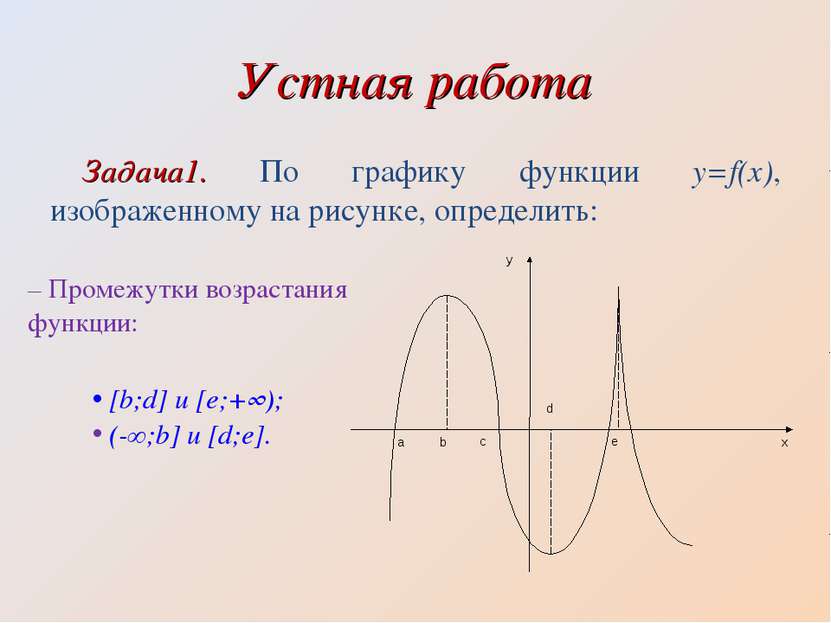
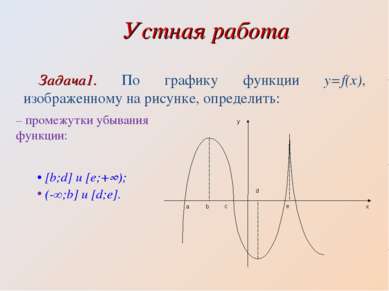Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить: – промежутки убывания функции: [b;d] и [e;+∞); (-∞;b] и [d;e].
Cлайд 16
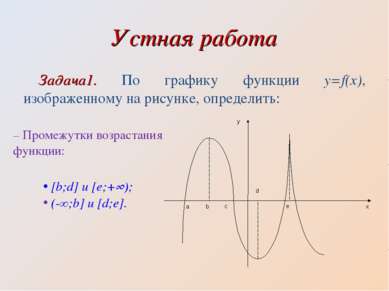Устная работа Задача1. По графику функции y=f(x), изображенному на рисунке, определить: – Промежутки возрастания функции: [b;d] и [e;+∞); (-∞;b] и [d;e].
Cлайд 17
Отлично! Далее
Cлайд 18
Подумай ещё!
Cлайд 19
Отлично! Далее
Cлайд 20
Подумай ещё!
Cлайд 21
Отлично! Далее
Cлайд 22
Подумай ещё!
Cлайд 23
Отлично! Далее
Cлайд 24
Подумай ещё!
Cлайд 25
Отлично! Далее
Cлайд 26
Подумай ещё!
Cлайд 27
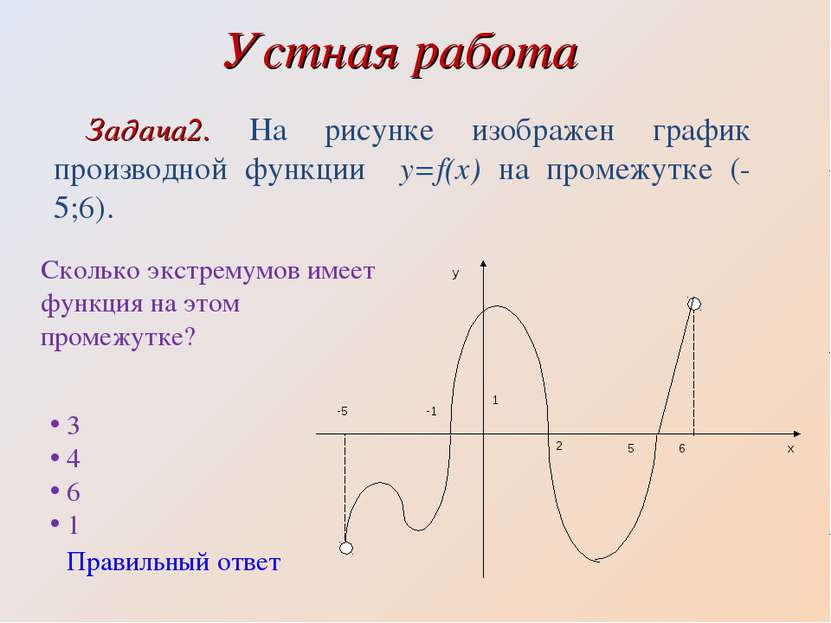
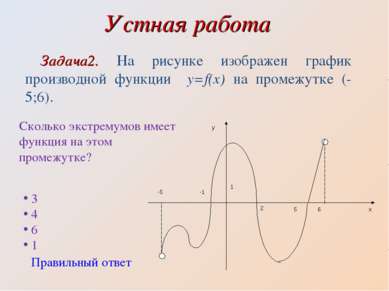Устная работа Задача2. На рисунке изображен график производной функции y=f(x) на промежутке (-5;6). Сколько экстремумов имеет функция на этом промежутке? 3 4 6 1 Правильный ответ
Cлайд 28
Правильный ответ 3
Cлайд 29
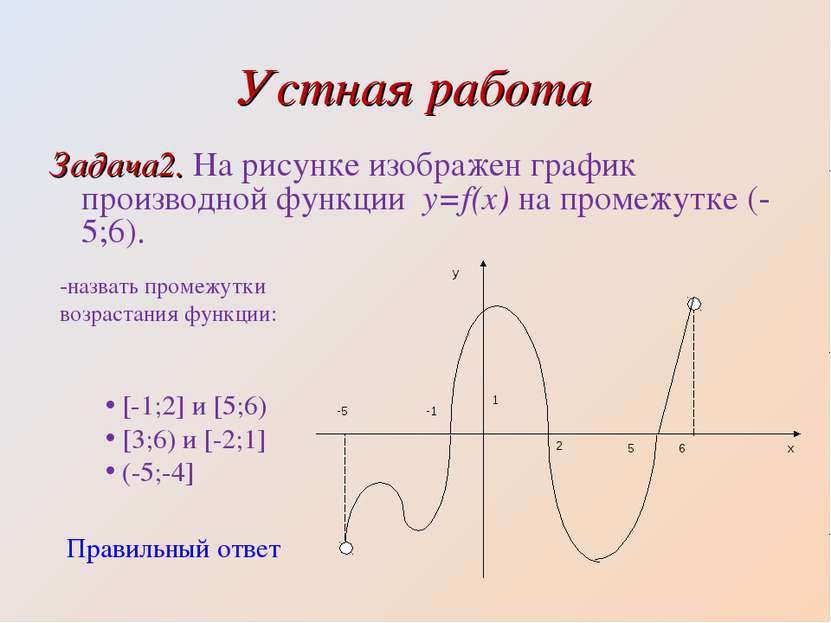
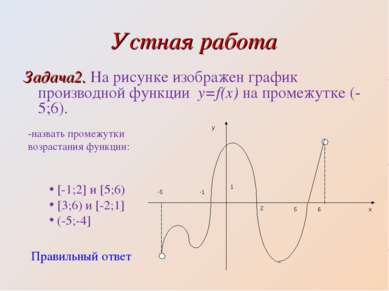Устная работа Задача2. На рисунке изображен график производной функции y=f(x) на промежутке (-5;6). -назвать промежутки возрастания функции: [-1;2] и [5;6) [3;6) и [-2;1] (-5;-4] Правильный ответ
Cлайд 30
![Правильный ответ [-1;2] и [5;6)](https://bigslide.ru/images/32/31084/960/img29.jpg "Правильный ответ [-1;2] и [5;6)")
Правильный ответ [-1;2] и [5;6)
Cлайд 31
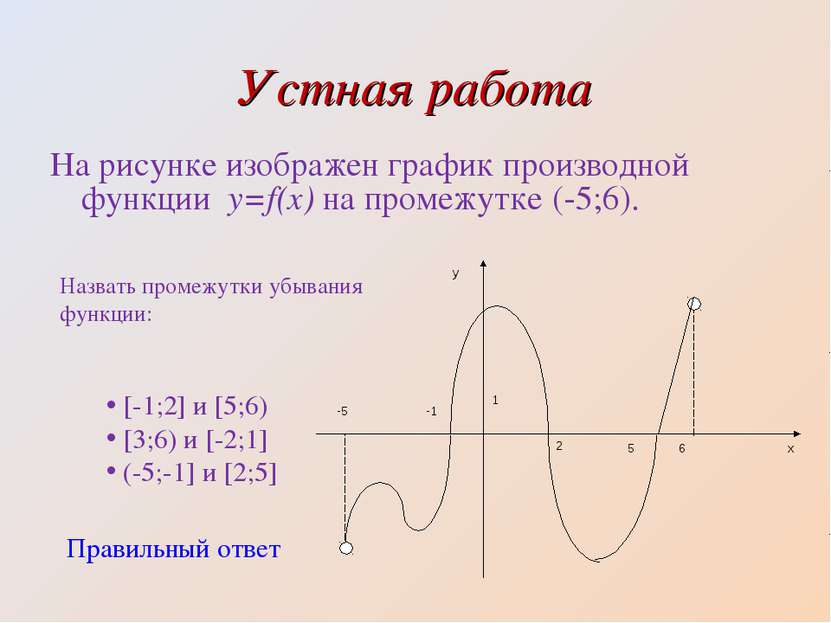
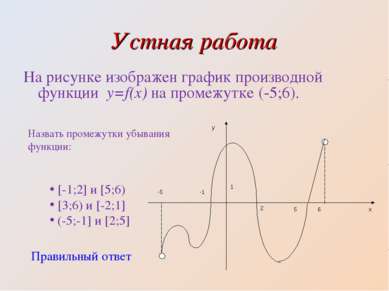Устная работа На рисунке изображен график производной функции y=f(x) на промежутке (-5;6). Назвать промежутки убывания функции: [-1;2] и [5;6) [3;6) и [-2;1] (-5;-1] и [2;5] Правильный ответ
Cлайд 32
![Правильный ответ (-5;-1] и [2;5]](https://bigslide.ru/images/32/31084/960/img31.jpg "Правильный ответ (-5;-1] и [2;5]")
Правильный ответ (-5;-1] и [2;5]
Cлайд 33
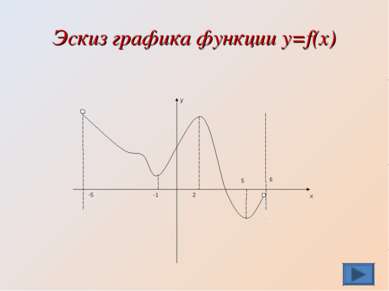
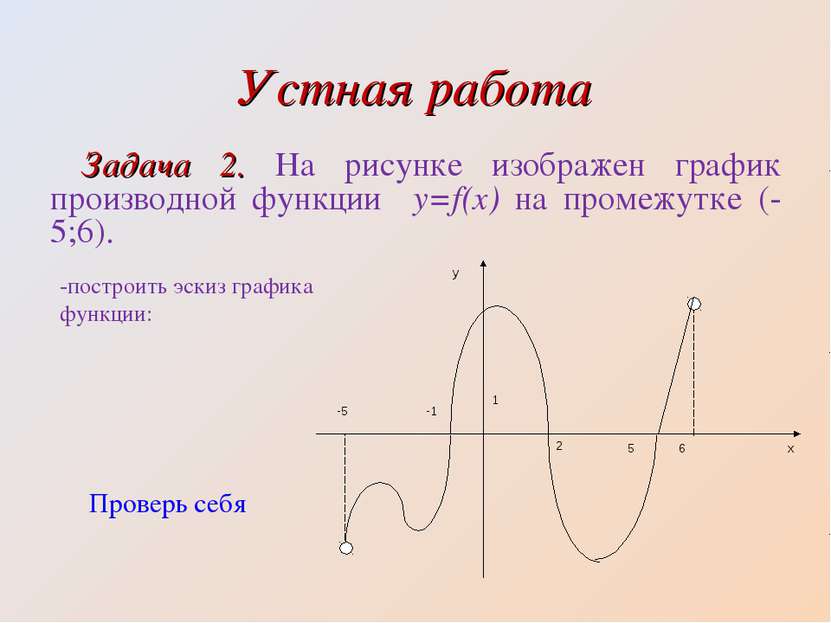
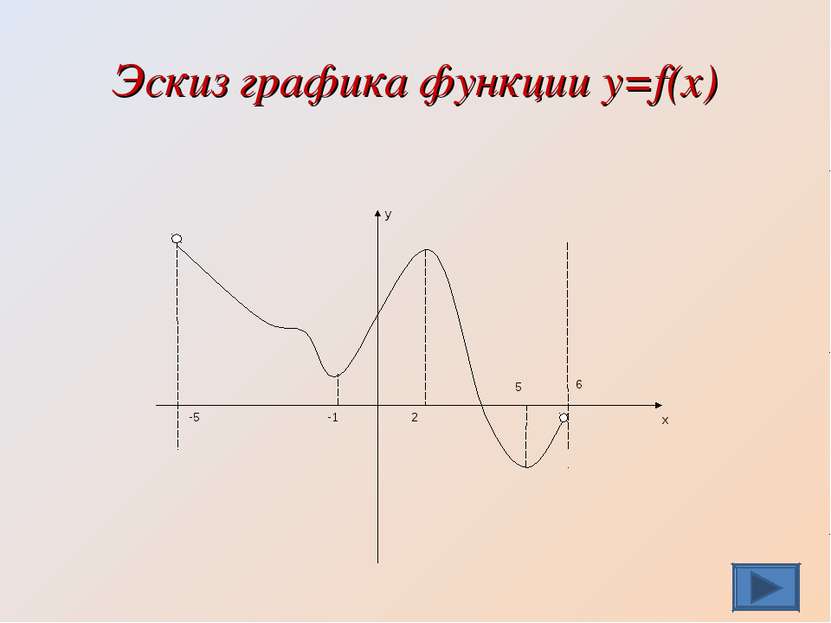
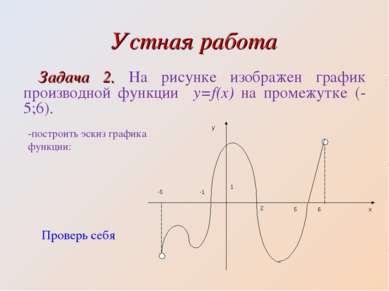Устная работа Задача 2. На рисунке изображен график производной функции y=f(x) на промежутке (-5;6). -построить эскиз графика функции: Проверь себя
Cлайд 34
Эскиз графика функции y=f(x)
Cлайд 35
Устная работа Задача3. Найти асимптоты графика функции Проверь себя
Cлайд 36
Ответ х=2 – вертикальная асимптота у=х – наклонная асимптота
Cлайд 37
Самостоятельная работа учащихся Класс делится на 3 группы. Каждая группа учащихся получает задание на карточке. Первая группа – задание базового уровня. Вторая группа – задание основного уровня. Третья группа – задание продвинутого уровня. Задание: Исследовать функцию с помощью производной и построить ее график. Исследовав функцию с помощью производной и построив ее график на листе бумаги, учащиеся сканируют свою работу и сохраняют ее на Smart – доске. Осуществляют самопроверку с помощью программы МаthCAD. Уровни
Cлайд 38
Уровни базовый уровень основной уровень продвинутый уровень
Cлайд 39
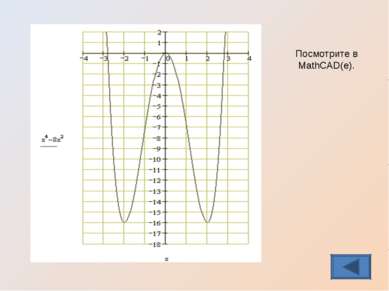
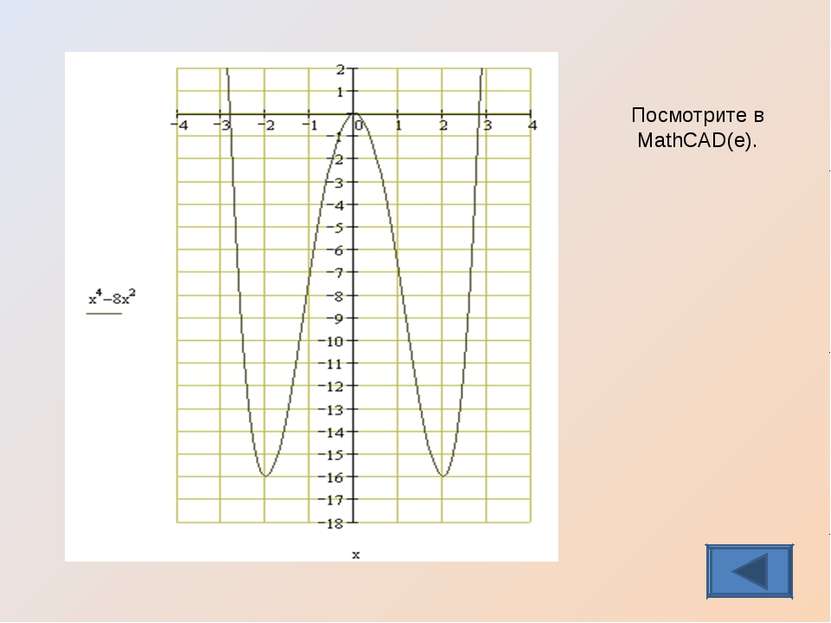
Задание группе 1 Базовый уровень: Исследовать функцию и построить ее график у = x4 – 8x2 Проверь себя Назад Справка
Cлайд 40
Задание группе 2 Основной уровень: Исследовать функцию и построить ее график Проверь себя Назад Справка
Cлайд 41
Задание группе 3 Продвинутый уровень: Исследовать функцию и построить ее график Проверь себя Назад Справка
Cлайд 42
Вспомните план исследования: 1.Область определения функции. 2.Множество значений функции. 3.Чётность. 4.Периодичность. 5.Первая производная: по ней определяются участки монотонности и точки экстремума. 6.Вторая производная: по ней определяются участки выпуклости и вогнутости и точки перегиба. 7.Точки пересечения с осями координат. 8.Таблица значений. . Назад
Cлайд 43
Вспомните план исследования: 1.Область определения функции. 2.Множество значений функции. 3.Чётность. 4.Периодичность. 5.Первая производная: по ней определяются участки монотонности и точки экстремума. 6.Вторая производная: по ней определяются участки выпуклости и вогнутости и точки перегиба. 7.Точки пересечения с осями координат. 8.Таблица значений. . Назад
Cлайд 44
Вспомните план исследования: 1.Область определения функции. 2.Множество значений функции. 3.Чётность. 4.Периодичность. 5.Первая производная: по ней определяются участки монотонности и точки экстремума. 6.Вторая производная: по ней определяются участки выпуклости и вогнутости и точки перегиба. 7.Точки пересечения с осями координат. 8.Таблица значений. . Назад
Cлайд 45
Проверь себя Замечаем, что функция четная и ее график симметричен оси ОУ, достаточно исследовать ее на интервале от 0 до +∞ . Данные исследования заносим в таблицу: График х ( -∞ , -2) -2 ( -2, 0 ) 0 ( 0, 2 ) 2 ( 2, +∞) f’ (x) - 0 + 0 - 0 + f (x) убывает -16 возрастает 0 убывает -16 возрастает
Cлайд 46
Посмотрите в MathCAD(е).
Cлайд 47
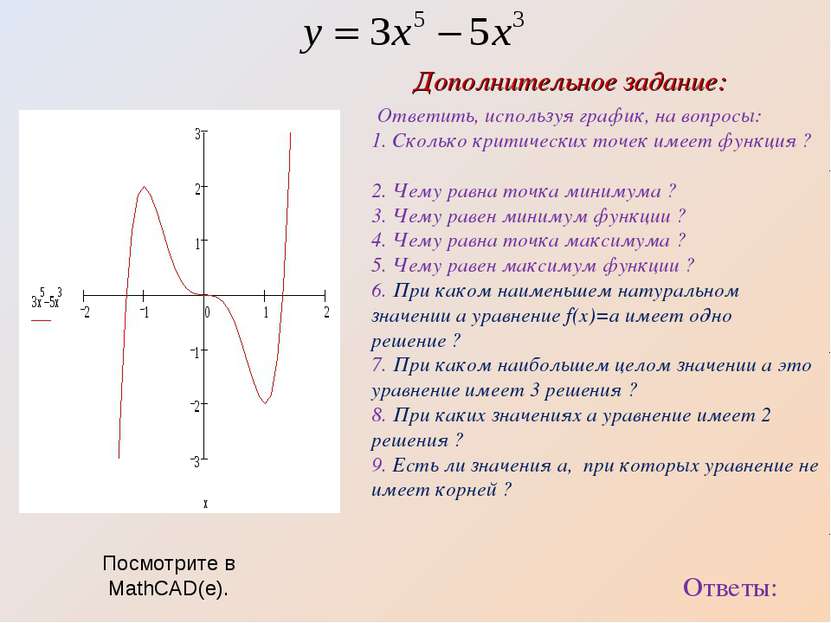
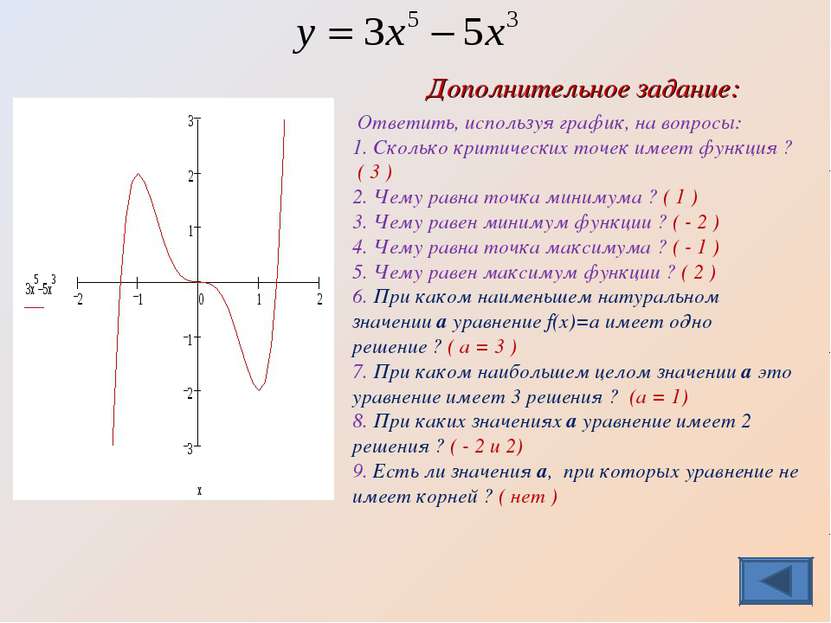
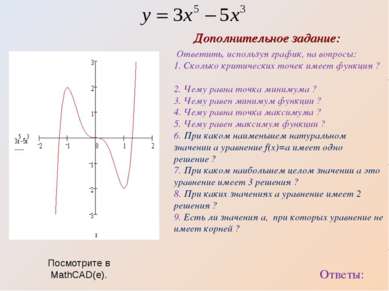Ответить, используя график, на вопросы: 1. Сколько критических точек имеет функция ? 2. Чему равна точка минимума ? 3. Чему равен минимум функции ? 4. Чему равна точка максимума ? 5. Чему равен максимум функции ? 6. При каком наименьшем натуральном значении а уравнение f(x)=a имеет одно решение ? 7. При каком наибольшем целом значении а это уравнение имеет 3 решения ? 8. При каких значениях а уравнение имеет 2 решения ? 9. Есть ли значения а, при которых уравнение не имеет корней ? Ответы: Дополнительное задание: Посмотрите в MathCAD(е).
Cлайд 48
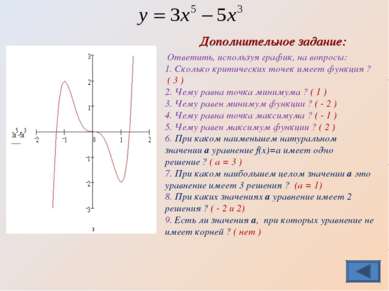Ответить, используя график, на вопросы: 1. Сколько критических точек имеет функция ? ( 3 ) 2. Чему равна точка минимума ? ( 1 ) 3. Чему равен минимум функции ? ( - 2 ) 4. Чему равна точка максимума ? ( - 1 ) 5. Чему равен максимум функции ? ( 2 ) 6. При каком наименьшем натуральном значении а уравнение f(x)=a имеет одно решение ? ( а = 3 ) 7. При каком наибольшем целом значении а это уравнение имеет 3 решения ? (а = 1) 8. При каких значениях а уравнение имеет 2 решения ? ( - 2 и 2) 9. Есть ли значения а, при которых уравнение не имеет корней ? ( нет ) Дополнительное задание:
Cлайд 49
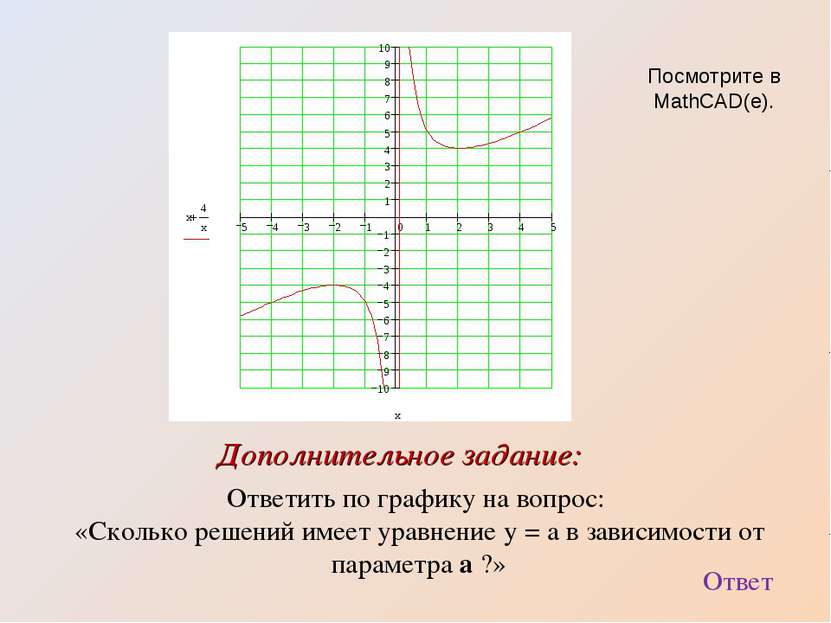
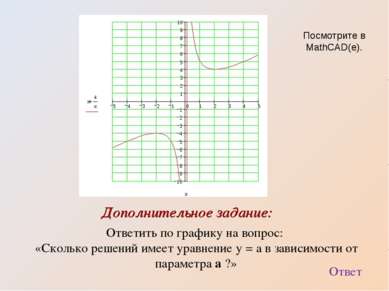Ответить по графику на вопрос: «Сколько решений имеет уравнение у = а в зависимости от параметра а ?» Дополнительное задание: Ответ Посмотрите в MathCAD(е).
Cлайд 50
Ответ: Если а = ± 4, то одно решение. Если |а| > 4, то два решения. Если -4
Cлайд 51
Обобщение Графики функций можно строить «по точкам». Однако при таком способе построения можно пропустить важные особенности графика. Можно строить график функции с помощью преобразований: сдвига прямой на а единиц; растяжения прямой от точки О с коэффициентом k; центральной симметрии относительно точки О; симметрии относительно оси абсцисс и оси ординат. А можно строить график методом исследования функции с помощью производной. Ход урока Далее
Cлайд 52
Итог Вот что сказал Декарт по поводу методов: «Под методом же я разумею точные и простые правила, строгое соблюдение которых всегда препятствует принятию ложного за истинное, и без излишней траты умственных силах, но постепенно и непрерывно увеличивая знания, способствует тому, что ум достигает истинного познания всего, что доступно.» Далее Методы математического анализа позволяют строить достаточно точный график заданной функции, если только удается хорошо изучить свойства этой функции.
Cлайд 53
Математика развивалась стремительно, но без понятия производной многие исследования не имели смысла. В 1679 году Пьер Ферма находил экстремумы функции, касательные, наибольшие и наименьшие значения функций. Но в своих записях он использовал сложнейшую символику Виета, и поэтому эти исследования не привели к созданию теории интегральных и дифференциальных исчислений. В 1736 году Исаак Ньютон получил теорию интегральных и дифференциальных исчислений методом флюксий (производных). Но вся теория была осмыслена с точки зрения физики. Математики хотели строгих логических обоснований. Современник Ньютона Лейбниц предложил новый подход к математическому анализу. Он ввёл обозначения дифференциала, интеграла, функции, такие понятия как ордината, абсцисса, координата. Но в его теории было много “тёмных мест”. И вот в 18 веке величайший математик Леонард Эйлер создал теорию дифференциальных и интегральных исчислений, и в таком виде она изучается и по сей день. Историческая справка Ход урока Далее
Cлайд 54
Исследуя функцию с помощью производной, я научился находить : Область определения функции; Определять четность функции; Критические точки и выделять из них точки экстремума; Промежутки монотонности функции; Точки перегиба; Промежутки выпуклости; Строить график функции Рефлексия Ответив на вопросы, оцените свои умения.
Cлайд 55
Спасибо за урок До свидания!!! Удачи вам!!!
Cлайд 56
Литература Программы для общеобразовательных школ, гимназий, лицеев. Математика, 5-11 классы; М. : Дрофа 2004. Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд . Алгебра и математический анализ 11. Учебник для углубленного изучения математики в общеобразовательных учреждениях. М.: Мнемозина, 2005. И.Н. Галицкий. Дидактические материалы по алгебре для 10 класса, учебное пособие для учащихся школ и классов с углубленным изучением математики. М.: Просвещение, 1998. И.Н. Галицкий и др. Методическое пособие для учителя «Углубленное изучение алгебры и математического анализа в 10 классе». М.: Просвещение, 2000.
