X
Код презентации скопируйте его
Построение графика неявно заданной функции на примере лемнискаты Бернулли
Скачать эту презентацию
Презентация на тему Построение графика неявно заданной функции на примере лемнискаты Бернулли
Скачать эту презентациюCлайд 1
Тема: «Построение графика неявно заданной функции на примере лемнискаты Бернулли» Проект Гузь Ольги
Cлайд 2
Содержание. 1.Определение функции заданной неявно. 2.Определение лемнискаты. 3.Вывод уравнения лемнискаты. 4.Преобразование уравнения лемнискаты. 5.Уравнение лемнискаты в полярной системе координат. 6.Исследование уравнения лемнискаты. 7.Построение лемнискаты. 8. Применение лемнискаты. 9.Краткая историческая справка.
Cлайд 3
Определение неявно заданной функции Рассмотрим функцию, заданную неявно уравнением F(x ,y)=0. В зависимости от того, какой является функция F(x ,y)-алгебраической или трансцендентной,- кривые также делятся на алгебраические и трансцендентные. Примеры, лемниската Бернулли.
Cлайд 4
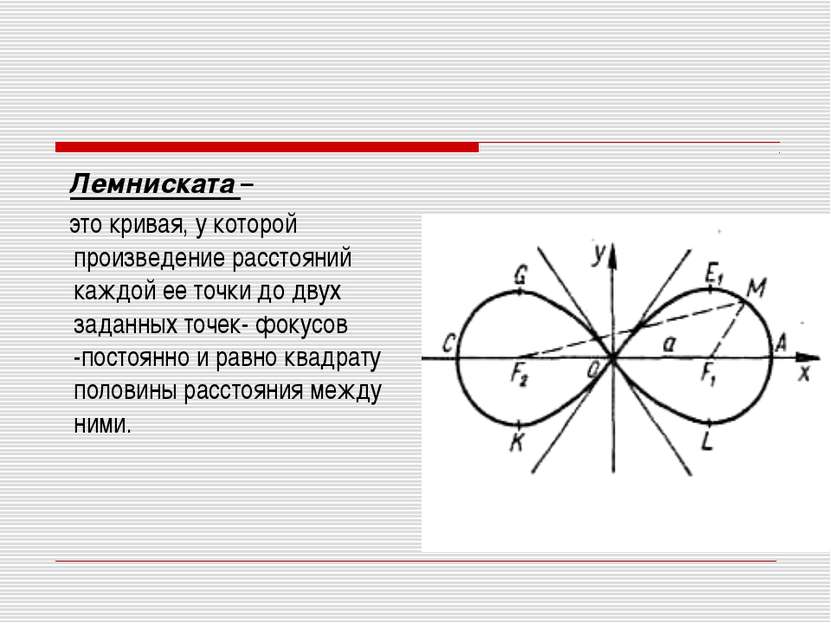
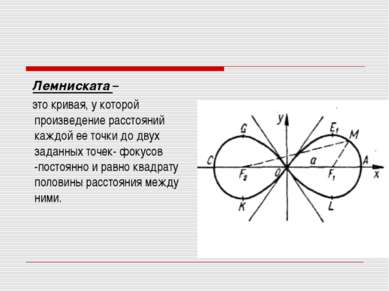Лемниската – это кривая, у которой произведение расстояний каждой ее точки до двух заданных точек- фокусов -постоянно и равно квадрату половины расстояния между ними.
Cлайд 5
Пусть фокусы имеют координаты: F1(-a;0) и F2 (а;0); М(х, у) - произвольная точка геометрического места, то по условию Подставляя в это равенство выражения получим искомое уравнение данного геометрического места
Cлайд 6
Дальнейшая цель- получить уравнение лемнискаты Бернулли в более простом виде. Возводя в квадрат обе части уравнения и группируя члены, находим отсюда
Cлайд 7
Преобразуя последнее уравнение, имеем: или в окончательном виде Мы получили уравнение лемнискаты в декартовой системе координат.
Cлайд 8
Т.к х и у входят в это уравнение только в чётных степенях, то лемниската симметрична относительно координатных осей. Построить график данной функции затруднительно. Запишем это же уравнение в полярной системе координат.
Cлайд 9
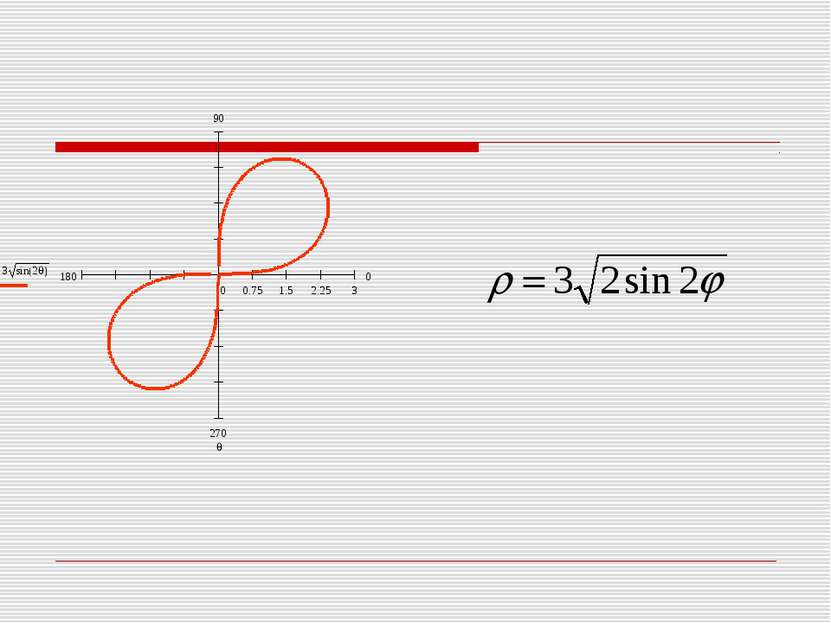
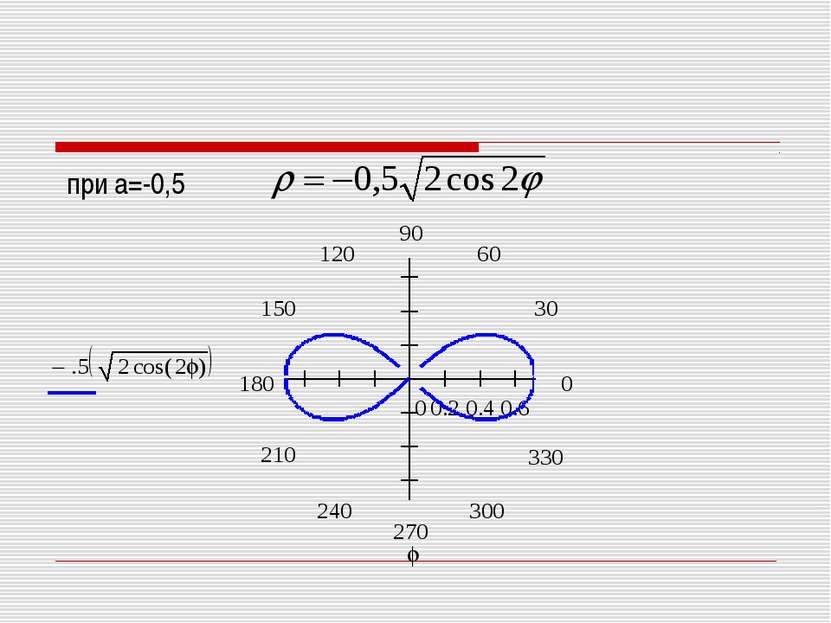
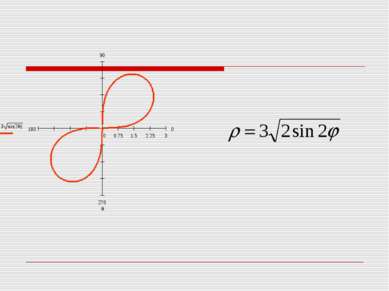
Поскольку х =ρ cos φ, у = ρ sinφ, х2+у2= ρ2, то уравнение лемнискаты в полярных координатах примет вид ρ 4=2а2 ρ(cos2φ- sin2φ) или ρ 2=2а2 cos2φ.
Cлайд 10
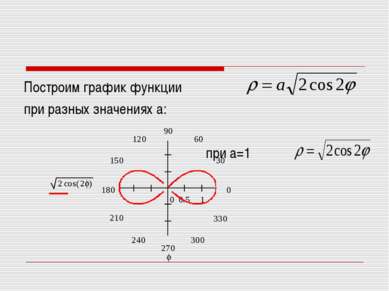
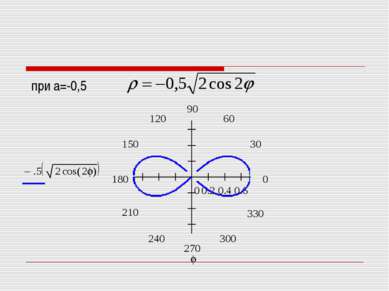
ρ 2=2а2 cos2φ Из этого уравнения видно, что при φ=0. Если φ увеличивается в пределах от 0 до , то ρ уменьшается от до ρ=0. Если , то ρ принимает мнимые значения. Это означает, что на лемнискате нет точек, для которых φ меняется в указанных пределах.
Cлайд 11
Построим график функции при разных значениях а: при а=1
Cлайд 12
Cлайд 13
при а=-0,5
Cлайд 14
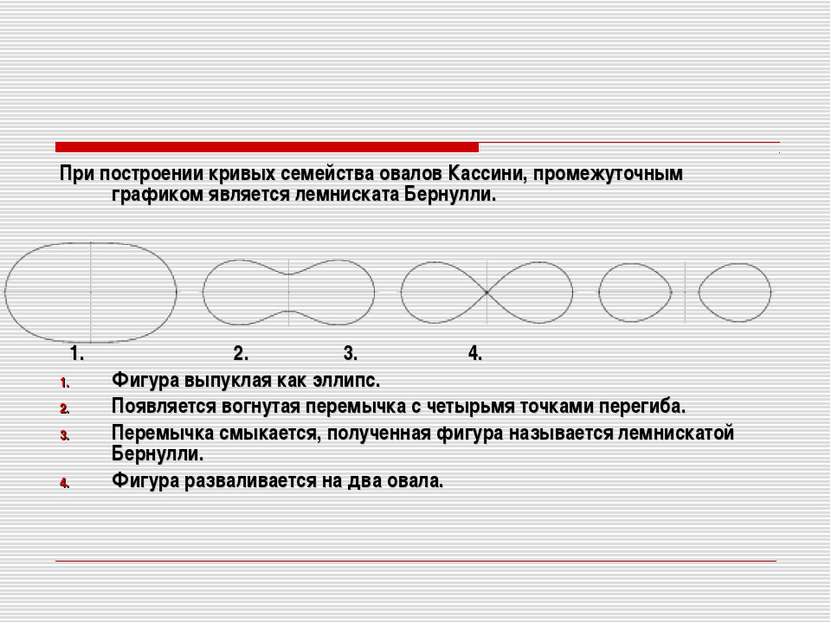
При построении кривых семейства овалов Кассини, промежуточным графиком является лемниската Бернулли. 1. 2. 3. 4. Фигура выпуклая как эллипс. Появляется вогнутая перемычка с четырьмя точками перегиба. Перемычка смыкается, полученная фигура называется лемнискатой Бернулли. Фигура разваливается на два овала.
Cлайд 15
В технике лемниската применяется, в частности, в качестве переходной кривой на закруглениях малого радиуса, как это имеет место на железнодорожных линиях в горной местности и на трамвайных путях.
Cлайд 16
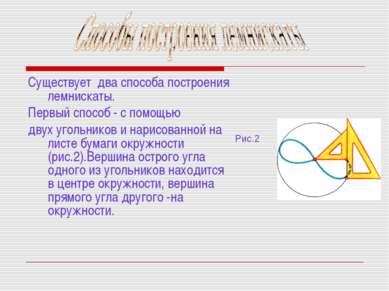Существует два способа построения лемнискаты. Первый способ - с помощью двух угольников и нарисованной на листе бумаги окружности (рис.2).Вершина острого угла одного из угольников находится в центре окружности, вершина прямого угла другого -на окружности. Рис.2
Cлайд 17
Второй способ - с помощью шарнирного устройства, две точки которого закреплены на плоскости (рис.3). Рис.3
Cлайд 18
Лемниската Бернулли. Ее автор – швейцарский математик Якоб Бернулли. Он дал этой кривой поэтическое название «лемниската». В античном Риме так называли бантик, с помощью которого прикрепляли венок к голове победителя на спортивных играх.
Cлайд 19
БЕРНУЛЛИ Якоб I (1654-1705). Швейцарский математик. Работал в Базельском университете. Работы посвящены математическому анализу, теории вероятностей и механике. В 1687 познакомился с первым мемуаром Лейбница по дифференциальному исчислению и применил его идеи к изучению ряда кривых, встречающихся в математике, механике, и выводу формулы радиуса кривизны плоской кривой. Ввел термин «интеграл».
Cлайд 20
♣ Вирченко Н.А. и др.Справочник «Графики функций»; Киев: Наук. думка, 1979г; ♣ И.И.Валуцэ «Математика для техникумов»; Москва, Издательство «Наука», 1980г; ♣ Маркушевич А.И. «Замечательные кривые»; Москва 1978 г.
Cлайд 21
Internet-ресурсы: WWW.Colledg.Ru; WWW.5ballov.Ru; WWW.bankreferatov.Ru; WWW.rubricon.com. Программное обеспечение: MS Word; MS Power Point;Windows Media; Nero Wave Editor; Сканер.
