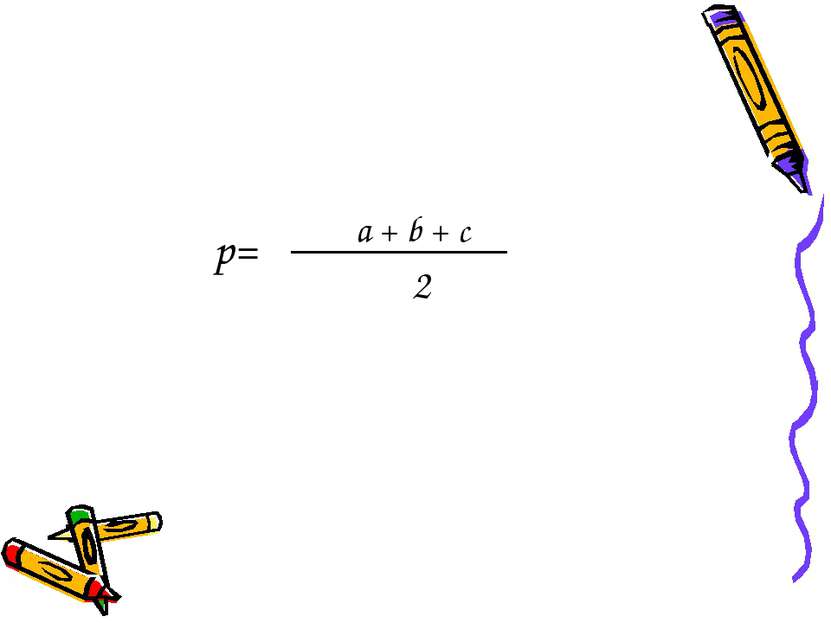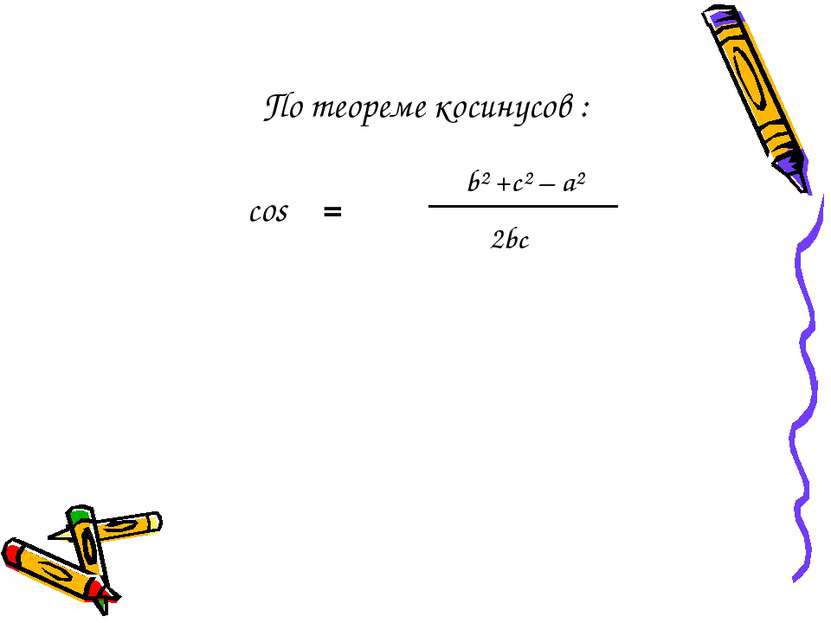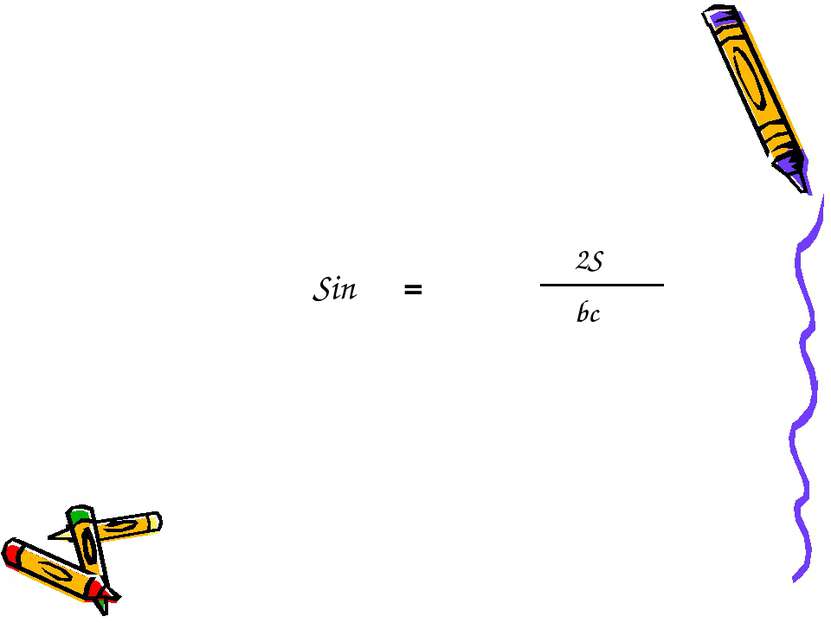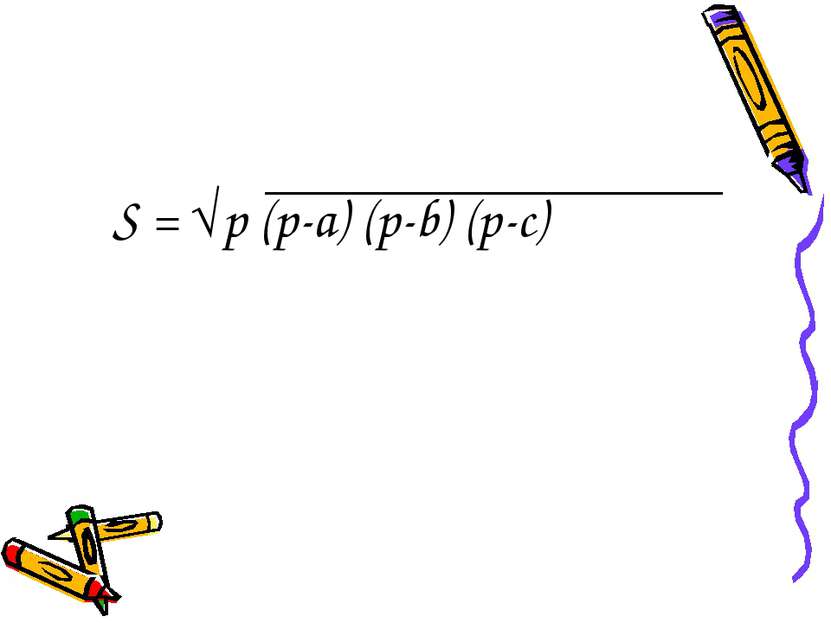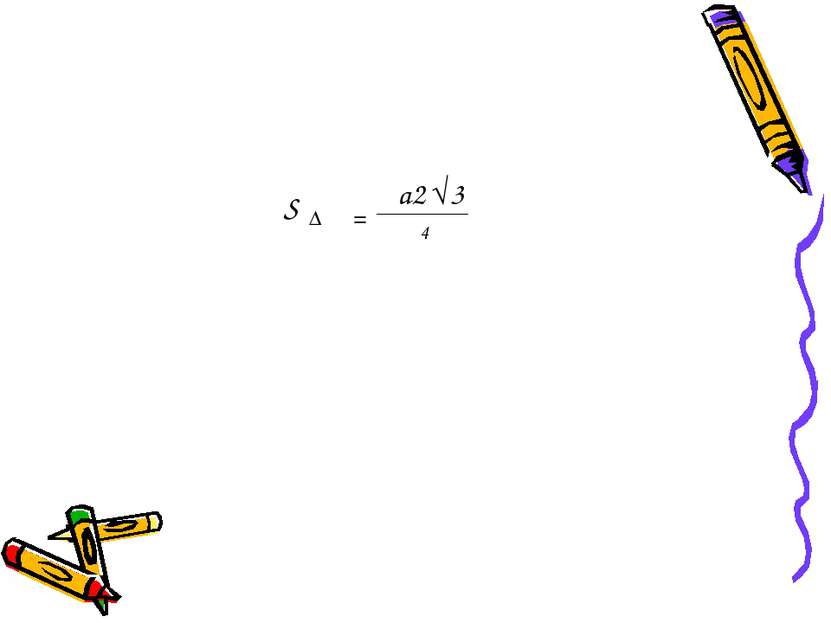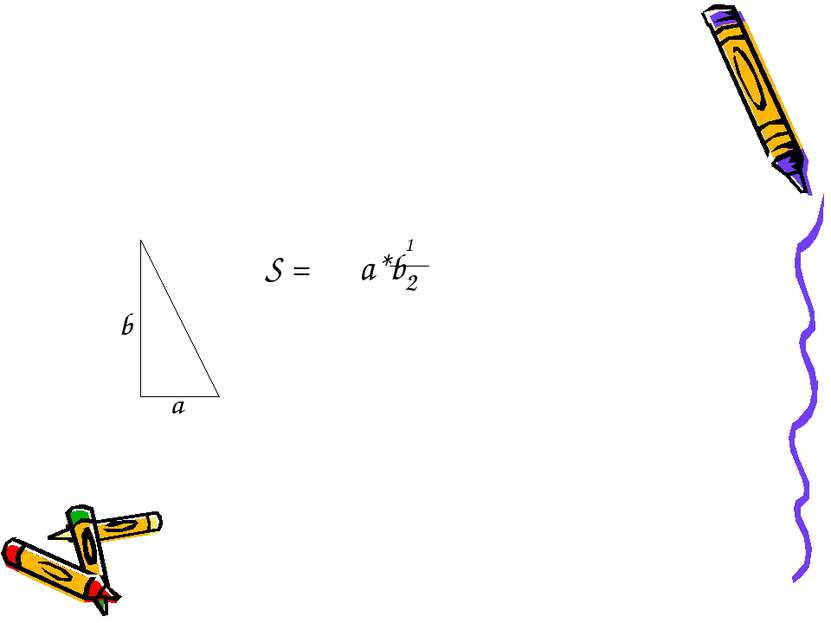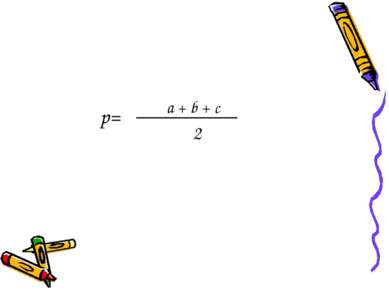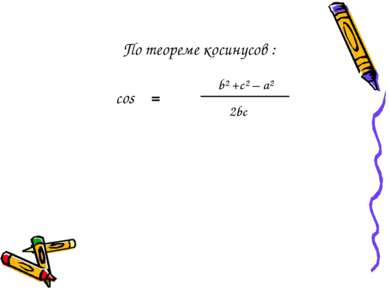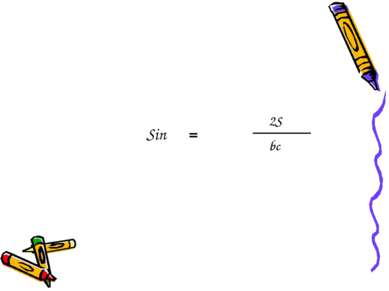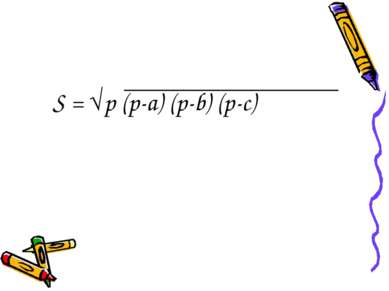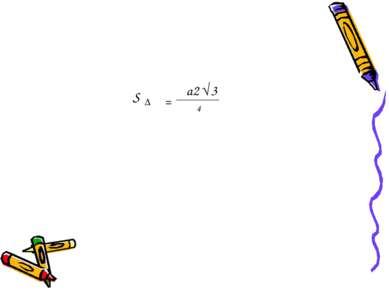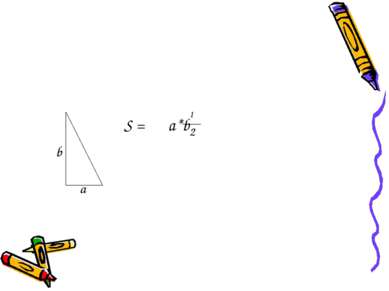X
Код презентации скопируйте его
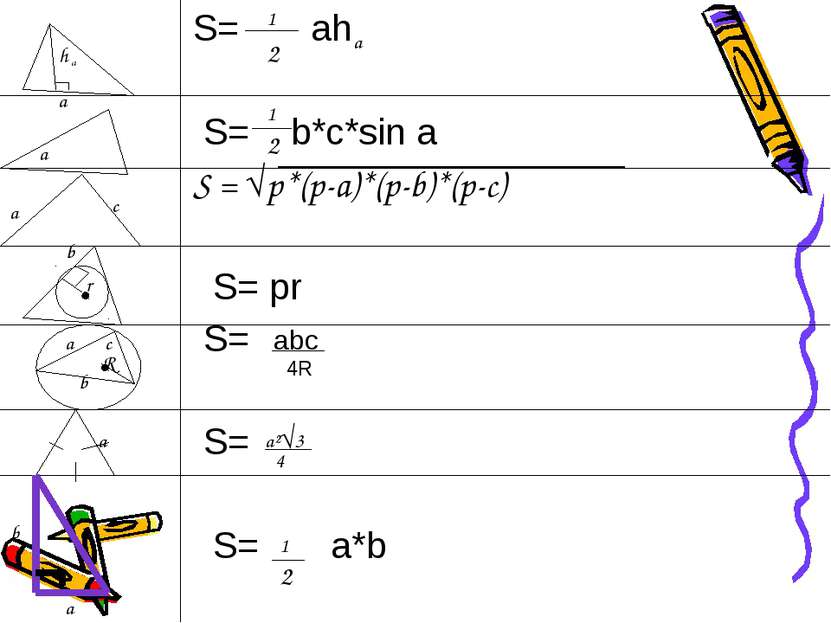
Формулы для вычисления площади треугольника
Скачать эту презентацию
Презентация на тему Формулы для вычисления площади треугольника
Скачать эту презентациюCлайд 1
Формулы для вычисления площади треугольника 9 класс
Cлайд 2
Цель урока: Познакомится с формулами для вычисления площадей треугольника: а) по стороне и высоте, проведенной к этой стороне; б) по двум сторонам и углу между ними; в) формулой Герона г ) Через радиус вписанной окружности и описанной окружности
Cлайд 3
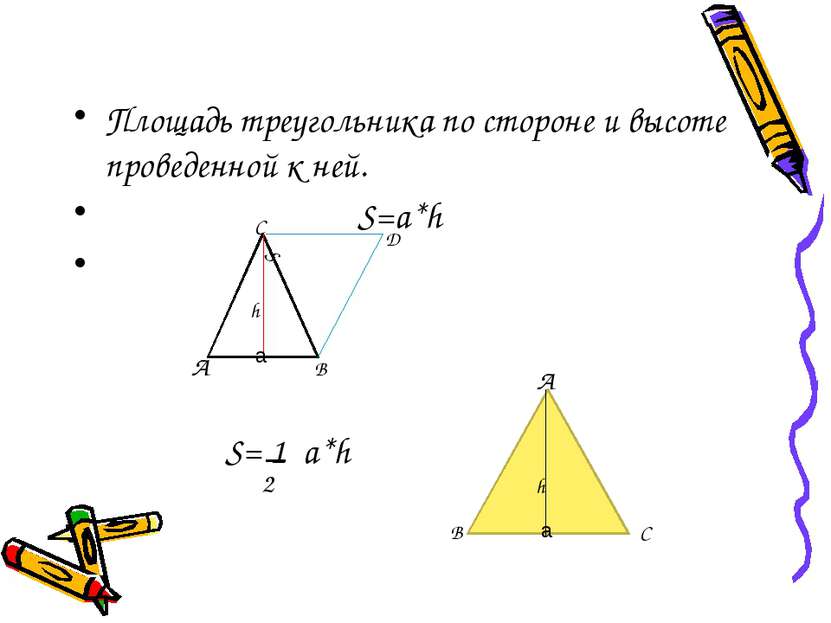
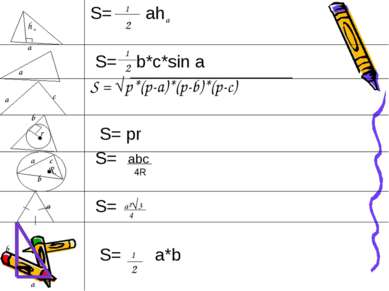
Площадь треугольника по стороне и высоте проведенной к ней. S=a*h А В С Д S h а а h А В С S= 1 a*h 2
Cлайд 4
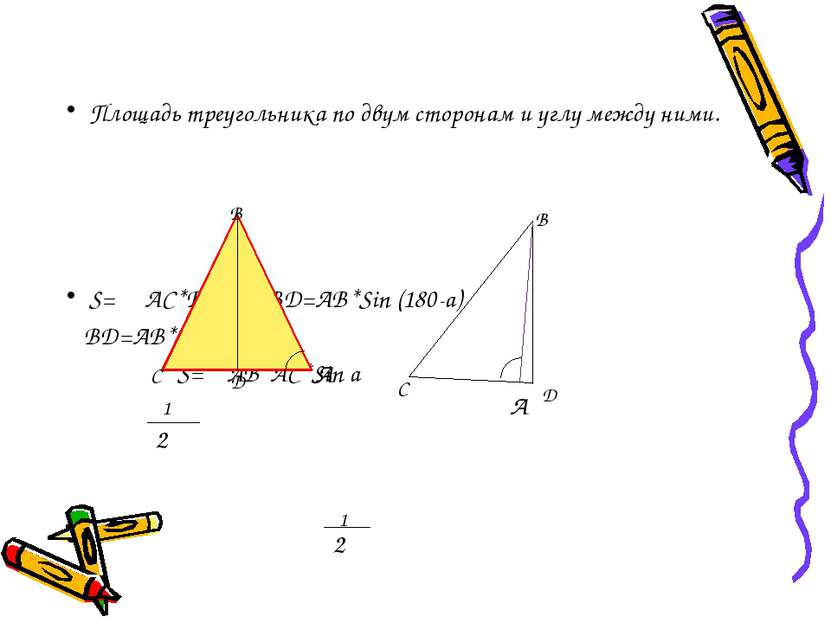
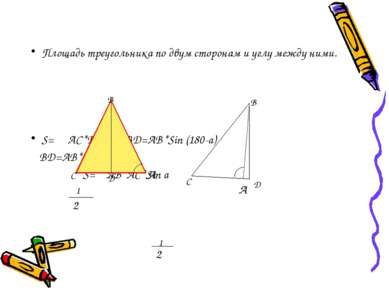Площадь треугольника по двум сторонам и углу между ними. S= АС*ВД ВД=АВ*Sin (180-a) ВД=АВ*Sin a S= АВ*АС*Sin a А А С С В В Д Д α α 1 2 1 2
Cлайд 5
Древнегреческий математик Герон Александрийский (I в. н.э.) Получил формулу для вычисления площади треугольника по его трём сторонам: S = √p (p-a) (p-b) (p-c)
Cлайд 6
Краткий вывод формулы Герона
Cлайд 7
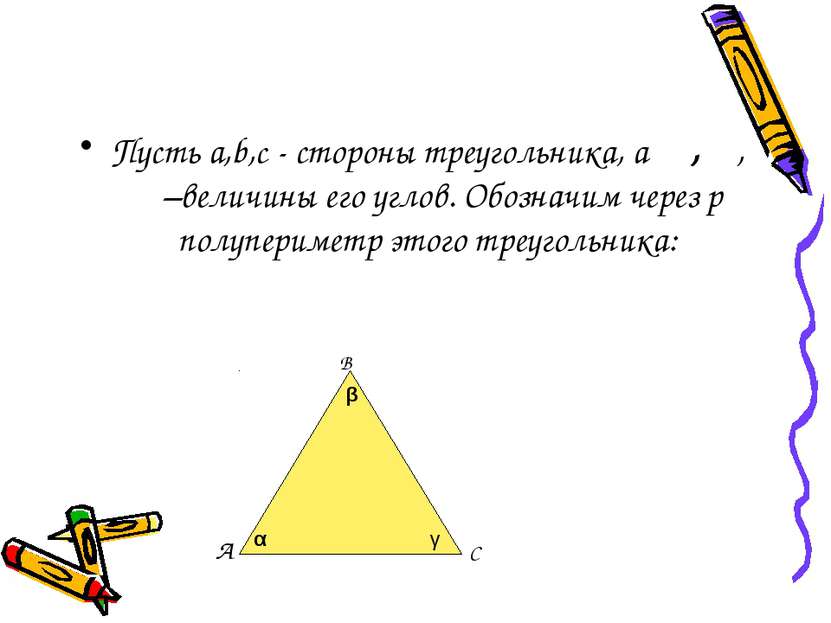
Пусть a,b,c - стороны треугольника, а α, β, γ –величины его углов. Обозначим через p полупериметр этого треугольника: С В А α β γ
Cлайд 8
p= a + b + c 2
Cлайд 9
По теореме косинусов : cos α= b² +c² – a² 2bc
Cлайд 10
Sin α = 2S bc
Cлайд 11
Подставляя найденные выражения Sin α и Cos α в формулу Sin² α + Cos² α = 1, получим: 2S bc ² b² + c² - a² 2bc ² + =1
Cлайд 12
Отсюда, применяя формулу разности квадратов, имеем: a + b + c 2 . b + c- a 2 . a + b - c 2 . a + c- b 2 = = p ( p – a )( p – b )( p - c)
Cлайд 13
S = √p (p-a) (p-b) (p-c)
Cлайд 14
Дано: АВС –треугольник АВ=ВС=АС=а Вывести:формулу площади треугольника S = a*h h= √ - =a √3 S= * a* a √3 а а а h 2 a 2 1 a² a² 4 2 1 2 2
Cлайд 15
∆ a2 √3 4 = S
Cлайд 16
S = a*b a b 1 2
Cлайд 17
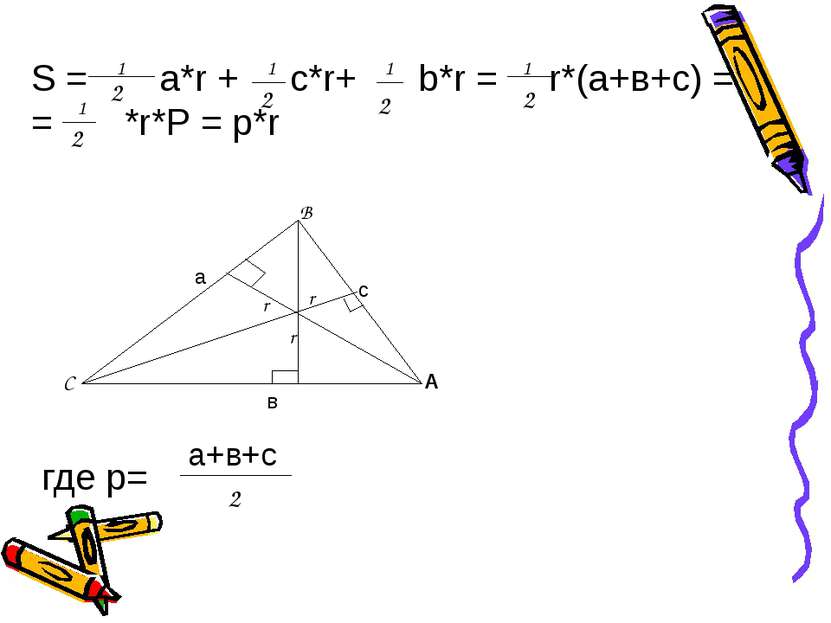
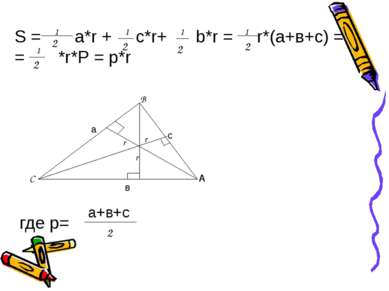В С S = a*r + c*r+ b*r = r*(а+в+с) = = *r*Р = р*r где p= А а в с r r r 1 2 2 1 1 2 1 2 1 2 а+в+с 2
Cлайд 18
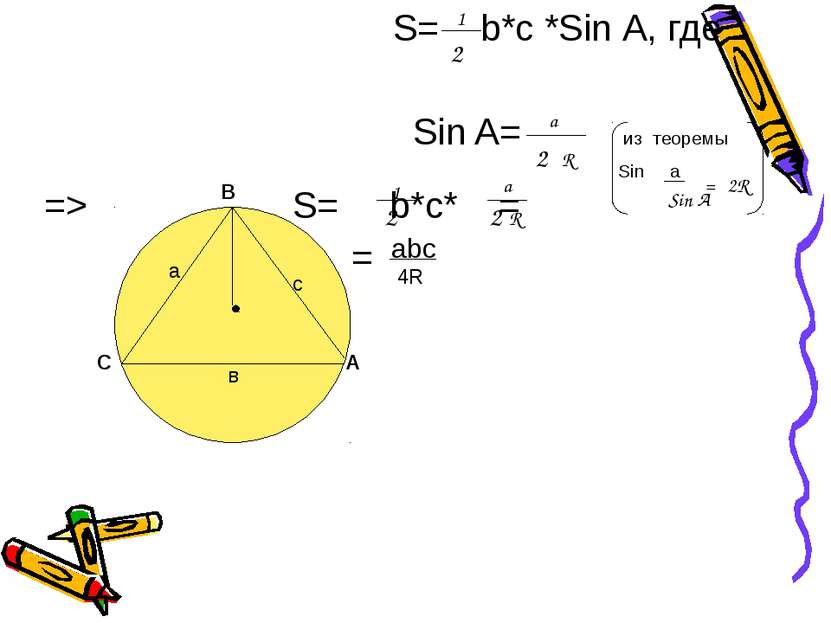
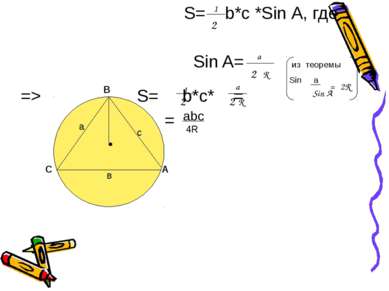S= b*с *Sin А, где Sin A= из теоремы Sin a => S= b*с* = = А в а с С В 2 1 a 2 R Sin A = 2R 1 2 a R 2 аbс 4R
Cлайд 19
S= ah S= b*c*sin a S = √p*(p-a)*(p-b)*(p-c) S= pr S= S= S= a*b 1 2 h a a a a 1 2 a b c r R a c b аbс 4R a a² √ 3 4 a b 1 2
Cлайд 20
Закрепление
Cлайд 21
№1 Дано: а=1,4см h=0,9см Найти: S -? ∆
Cлайд 22
№2 Дано: а=5см b=6см α = зо ° Найти: S -? ∆
Cлайд 23
№3 Дано: а=5 b=5 с=6 Найти: S -? ∆
Cлайд 24
Д/ З: п.124,125 №30(1), №27
Cлайд 25
Cлайд 26
Cлайд 27
