X
Код презентации скопируйте его
Геометрические задачи 7 класса в заданиях ОГЭ
Скачать эту презентацию
Презентация на тему Геометрические задачи 7 класса в заданиях ОГЭ
Скачать эту презентациюCлайд 1
Cлайд 2
Геометрические задачи 7 класса в вариантах ОГЭ
Cлайд 3
Цели урока: Сегодня мы с вами разберём несколько примеров по геометрии 7 класса, которые даются в ОГЭ-2015. Ведь действительно, Основной Государственный Экзамен — ОГЭ, рассчитан не только на знания 9 класса, но и на те знания, которые ученики получают в 7 и 8 классах по геометрии, и, начиная с 5 класса, по математике и алгебре. Поэтому, в модуле «Геометрия» есть задачи из курса 7 класса.
Cлайд 4
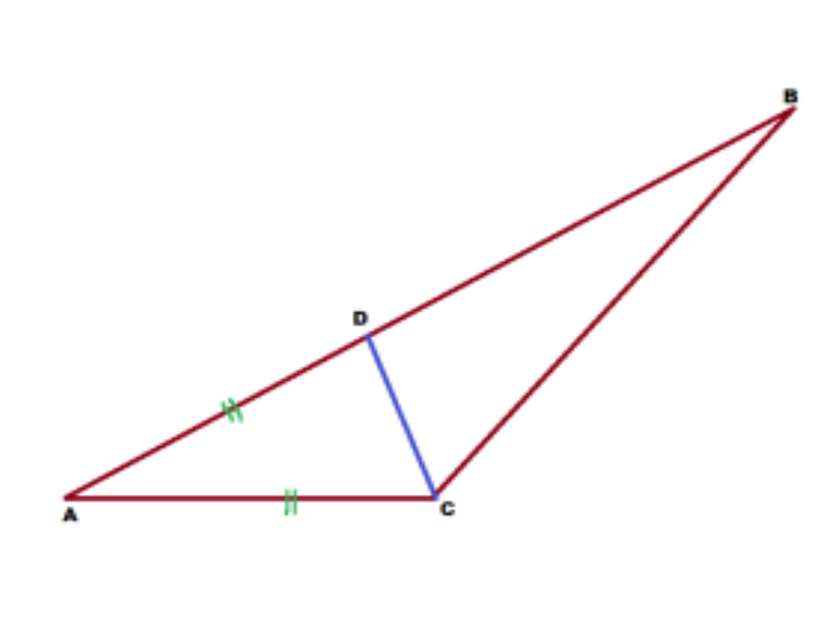
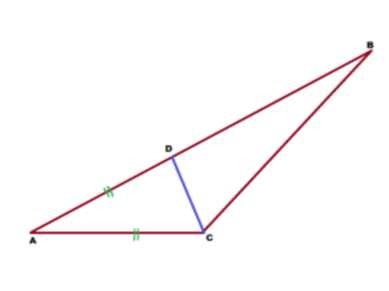
Задача 1. В треугольнике АВС точка D на стороне АВ выбрана так, что АС=AD. Угол А треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB.
Cлайд 5
Cлайд 6
Решение: Из треугольника ADC видно, что он равнобедренный, поскольку 2 боковые стороны его равны. А в равнобедренном треугольнике углы при основании равны. Значит, угол ADC равен углу АСВ. Но сумма внутренних углов треугольника равна 180°. Отсюда, сумма двух углов при основании равна 180-16=164°. Углы, как мы уже сказали, равны. Поэтому, каждый из них равен 164:2 = 82°. Угол АСВ по условию равен 134°. А если внутри угла провести луч, то он разделит угол на 2 угла, сумма градусных мер которых будет равна градусной мере первоначального угла. Т.е. Угол АСВ равен сумме углов АCD и DCB. Отсюда, угол DCB равен 134 — 82 = 52°. Ответ: угол DCB равен 52°.
Cлайд 7
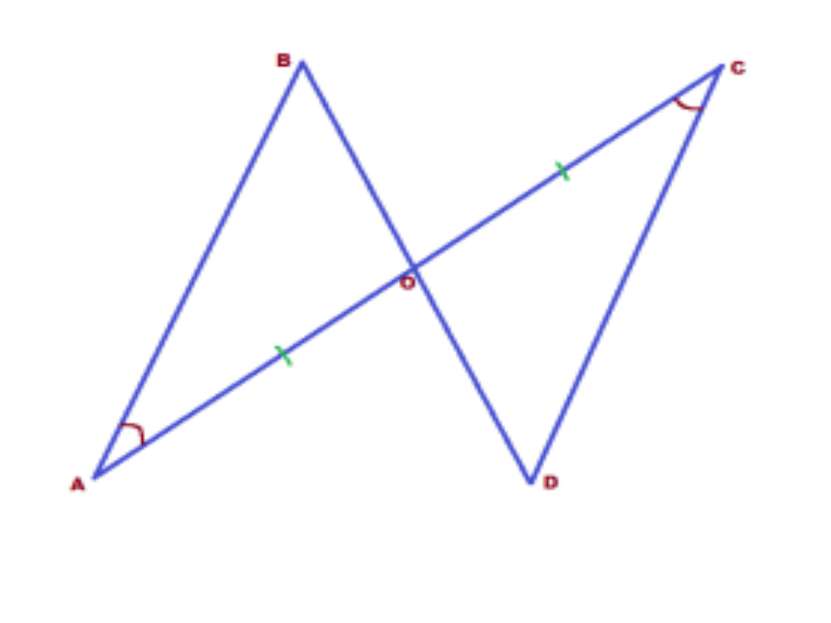
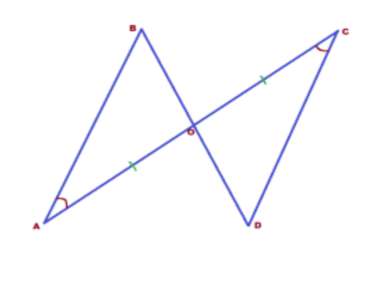
Задача 2. Два отрезка АС и BD пересекают в точке О. Причём, АО=СО и ∠А=∠С. Доказать, что треугольники АОВ и OC равны.
Cлайд 8
Cлайд 9
Доказательство: В искомых треугольниках есть по одной равной стороне и одному равному углу. Значит, согласно признакам равенства треугольников, нам необходимо ещё либо по одной равной стороне, либо по одному равному углу. Стороны как-то не проглядываются, а вот по равному углу можно ещё найти. Углы АОВ и DOC — вертикальные. А вертикальные углы, как мы знаем, равны. В каждом из треугольников мы имеем по равной стороне и двум равным углам, прилежащим к ней. Треугольники равны по 2 признаку.
Cлайд 10
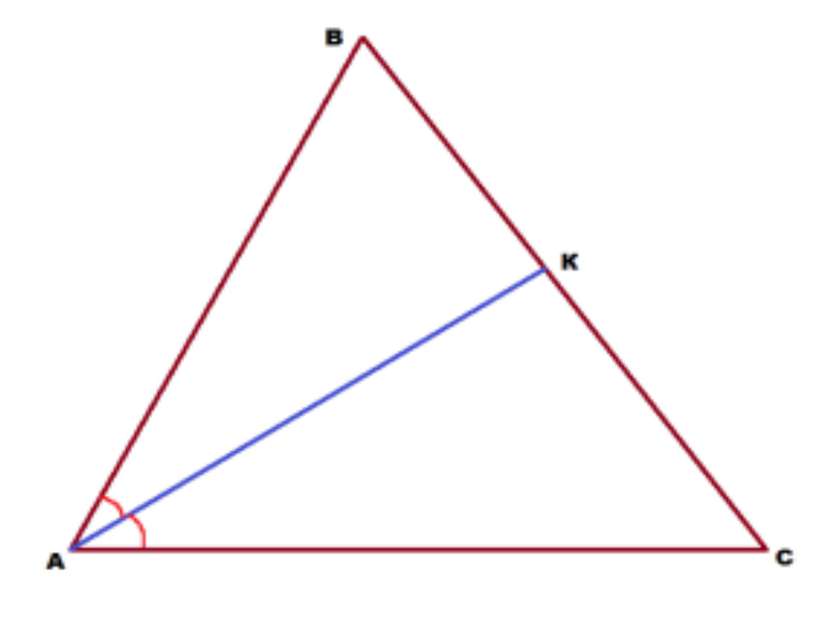
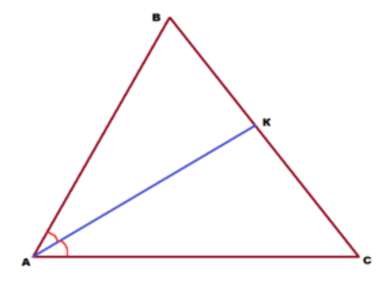
Задача 3. В треугольнике АВС проведена биссектриса АК. Угол АКС равен 94°, а угол АВС равен 62°. Найти угол С треугольника АВС.
Cлайд 11
Cлайд 12
Решение: Угол АКС является внешним для треугольника АВК и равным сумме двух внутренних углов, не смежных с ним, т.е. сумме углов В и ВАК. Отсюда мы можем найти угол ВАК. Он равен 94 — 62 = 32°. Поскольку АК — биссектриса угла А, то угол КАС тоже равен 32°. А теперь, рассматривая треугольник АКС и зная в нём 2 угла, можно найти третий. ∠С = 180 — 32 — 94 = 54°. Ответ: угол С равен 54°.
Cлайд 13
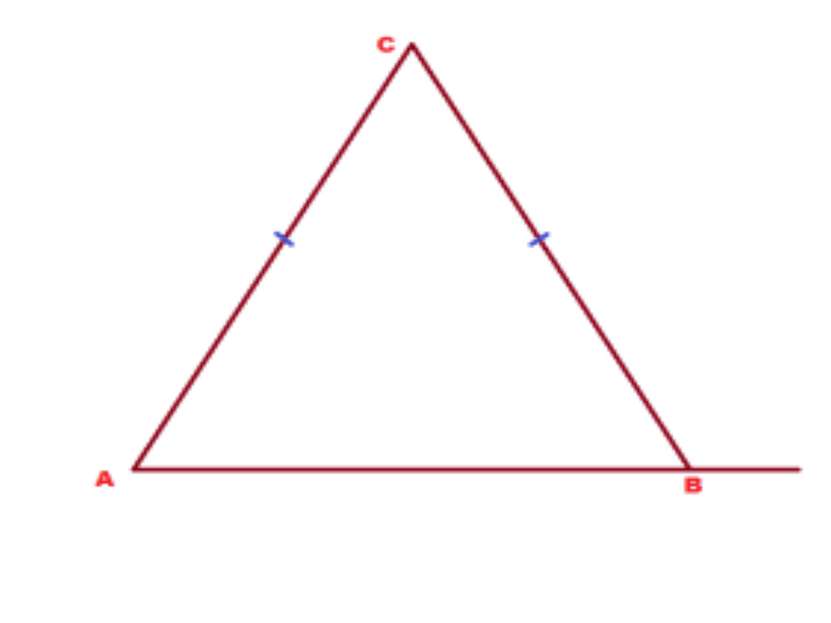
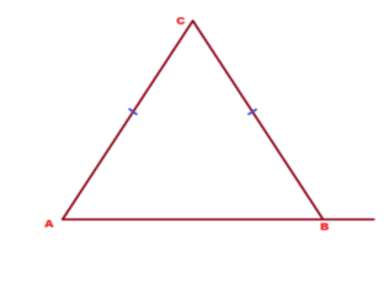
Задача 4. В треугольнике АВС боковые стороны АС и АВ равны между собой. Внешний угол при вершине В равен 110°. Найти угол С.
Cлайд 14
Cлайд 15
Решение: Внешний угол В равен 110°, значит, смежный с ним внутренний угол в треугольнике равен 180-10 = 70°. Но внутренний угол В равен углу А, как углы при основании равнобедренного треугольника. Значит, угол А равен 70°. А сумма внутренних углов треугольника равна 180°. И если 2 из них равны по 70, то на долю третьего угла С приходится 180 — 70 — 70 = 40°. Ответ: угол с равен 40°.
Cлайд 16
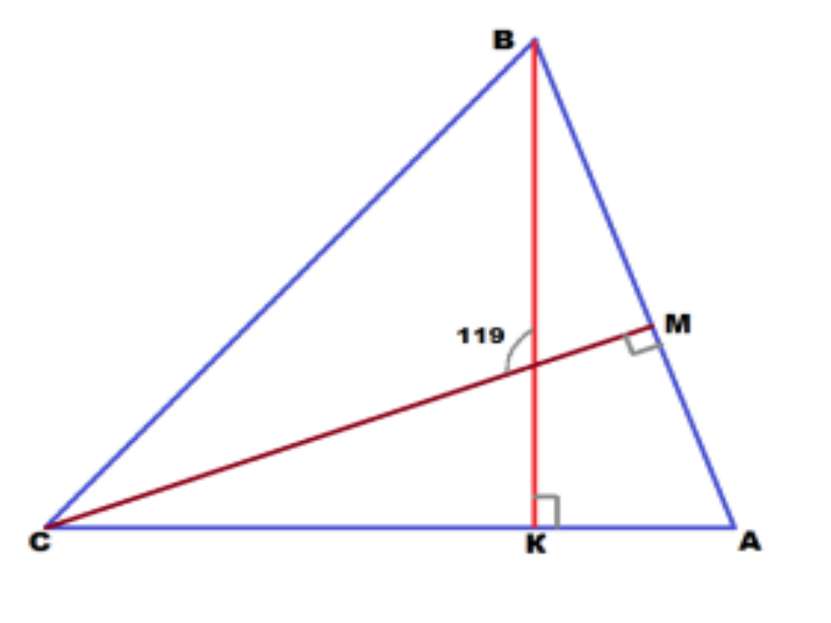
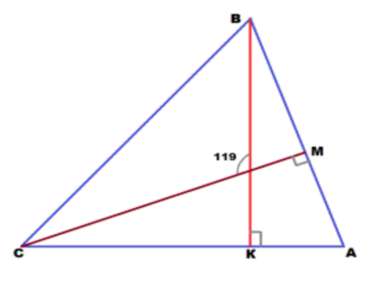
Задача 5. В треугольнике АВС проведены высоты, которые пересекаются в точке О. Угол СОВ равен 119°. Найти угол А.
Cлайд 17
Cлайд 18
Решение: Угол ВОМ смежный углу СОМ и равен 180-119 = 61°. Угол СМА внешний в треугольнике СМВ и равен сумме двух внутренних, не смежных с ним. Отсюда, угол ОВМ равен 90-61 = 29°. А из прямоугольного треугольника ВКА можно найти угол А, т.к. сумма острых углов в прямоугольном треугольнике равна 90°. Значит, угол А равен 90 — 29 = 61°. Ответ: угол А равен 61°.
Cлайд 19
