X
Код презентации скопируйте его
Задачи практического содержания
Скачать эту презентацию
Презентация на тему Задачи практического содержания
Скачать эту презентациюCлайд 1
ЗАДАЧИ ПРАКТИЧЕСКОГО СОДЕРЖАНИЯ Учитель математики Кидалова Лариса Леонидовна, МАОУ ЦО №47, Г. Иркутск
Cлайд 2
Решение задач практического содержания — один из способов повышения мотивации к изучению математике. Важное значение в процессе обучения математике имеет понимание школьниками практической значимости учебного материала, перспективы его использования. Для привития интереса к предмету необходимо, чтобы каждое новое понятие или положение находило применение в задачах практического характера, в реальной жизни. Именно это убеждает школьников в том, что математика наука полезная, необходимая во всех видах деятельности.
Cлайд 3
Под задачей с практическим содержанием понимается математическая задача, которая раскрывает приложения математики в окружающей нас действительности, в смежных дисциплинах, знакомит с ее использованием в организации, технологии и экономике современного производства, в сфере обслуживания, в быту, при выполнении трудовых операций. Задачи с практическим содержанием целесообразно использовать в процессе обучения для раскрытия многообразия применений математики в жизни, своеобразия отражения ею реального мира и достижения таких дидактических целей как: мотивация введения новых математических понятий и методов; иллюстрация учебного материала; закрепление и углубление знаний по предмету; формирование практических умений и навыков.
Cлайд 4
№1. В детском оздоровительном центре делают бассейн цилиндрической формы. Длина окружности его основания равна 36 м, высота – 1,2 м. Стены бассейна выкладывают плиткой. Сколько кг клея нужно приобрести, если на 1 м2 расходуется 2 кг клея? Решение. Развертка боковой поверхности цилиндра представляет прямоугольник со сторонами 36 м и 1,2 м. 36 · 1,2 = 43,2 (м2) – площадь боковой поверхности бассейна 43,2 · 2 = 46,4 (кг) – масса клея Ответ: 46,4 кг
Cлайд 5
№2. Решено стены учебной комнаты покрасить краской. Высота комнаты – 2,5 м, длина 8 м, ширина 6 м. Дверь имеет размеры: высота – 2 м, ширина – 0,9м. Найти стоимость работ, если действует сезонная скидка 10%. Стоимость приведена в таблице: Решение. 6 · 2,5 = 18 (м2) – площадь боковой стены; 8 · 2,5 = 20 (м2) – площадь задней стены; 18 · 2 + 20 · 2 = 36 + 40 = 76 (м2) – площадь всех стен; 2 · 0,9 = 1,8 (м2) – площадь двери; 76 – 1,8 = 74,2 (м2) – площадь для покраски; 74,2 · 55 = 4081 руб.; 4081 : 100 · 10 = 4081 · 0,1 = 408,1 (руб.) – скидка; 4081 – 408,1 = 3672,9 (руб.) – стоимость работ Ответ: 3672,9 руб. Цена в руб. за 1м2 от 1 до от 21 до свыше до свыше 70 65 60 55
Cлайд 6
№3. На дне аквариума прямоугольной формы лежит куб с ребром 15 см. При этом уровень воды в аквариуме 32,25 см. Каким будет уровень воды в аквариуме после того, как куб вынули? Длина аквариума 50 см, ширина 30см. Решение. 15 · 15 · 15 = 3375 (см3) – объем куба; 50 · 30 · 32,25 = 48375 (см3) - V воды в аквариуме; 48375 – 3375 = 45000 (см3) – объем без куба; т.к. V = a·b·c, 45000 = 15 · 30 · с, с = 30 Ответ: 30 см.
Cлайд 7
№4. Хозяйка квартиры решила покрасить стены чулана на высоту 1,5 м от пола. Какое количество краски (кг) нужно приобрести, если на 1 м2 расходуется 300 граммов краски (дверь 0,8 м на 2 м не красится). Длина чулана 3 м, ширина 2 м, высота 2,5. Решение. 2 · (2+3) · 1,5 = 2· 5· 1,5 = 15 (м2) – площадь боковой поверхности; 0,8 · 1,5 = 1,2 (м2) – площадь двери; 15 – 1,2 – 13,8 (м2) – площадь под покраску; 13,8 · 0,3 = 4,14 (кг) – масса краски; Ответ: 4,14 (кг)
Cлайд 8
№5. Стены и потолок ванной комнаты решили выложить кафельной плиткой. Какое количество клея нужно приобрести, если на 1 м2 расходуется 1,4 кг клея. Размеры комнаты: длина 3 м, ширина 2 м, высота 2,5 м. Дверь 0,8 м на 2 м. Решение. 2 · 3 = 6 (м2) – площадь потолка; 2 · 0,8 = 1,6 (м2) – площадь двери; 3 · 2 · 2,5 + 2 · 2,5 · 2 = 15 + 10 = 25 (м2) – площадь стен; 25 + 6 – 1,6 = 31 – 1,6 = 29,4 (м2) – площадь под покраску; 29,4 · 1,4 = 41,16 (кг) – масса клея. Ответ: 41,16 (кг)
Cлайд 9
№6. В детской школе искусств для класса хореографии оклеивают стены обоями, зал имеет форму прямоугольного параллелепипеда. С целью гигиены, обои начинают клеить на расстоянии 1,2 м от пола. Длина зала 15 м, высота 3,4 м, ширина 7,5 м. Сколько рулонов обоев шириной 1 м, длиной 10 м, нужно купить, если дверь шириной 0,8 м, высотой 2 м не оклеивают? На подбор рисунка берут обои с 15% запасом от необходимого количества. Решение. (15 + 7,5) · 2 · 2,2 = 99 (м2) – площадь боковых стен; 0,8 · 0,5 = 0,40 (м2) – площадь двери; 99 – 0,4 = 98,6 (м2) – площадь под заклейку; 1 · 10 = 10 (м2) – площадь 1-го рулона; 98,6 : 10 = 9,86 (рулонов); 9,86 · 1,15 = 11,339 рулонов ≈ 12 рулонов; Ответ: 12 рулонов
Cлайд 10
№7. Металлический гараж в форме прямоугольного параллелепипеда требуется окрасить снаружи краской. Расход краски 120 г на 1 м2. Стоимость 1 банки краски 240 руб. Каковы затраты на приобретение краски для окраски гаража, если длина его 5,5 м, ширина 4,2 м; высота – 2 м? Решение. 4,2 · 5,5 = 23,1 (м2) – площадь потолка; 5,5 · 2 · 2 + 4,2 · 2 · 2 = 22 + 16,8 = 38,8 (м2) – площадь стен; 23,1 + 38,8 = 61,9 (м2) – общая площадь для покраски; 61,9 · 0,12 = 7,428 (кг) – масса краски; 7,428 : 2 = 3,714 (банок), т.е. 4 банки; 4 · 240 = 960 (руб.) – затраты на краску. Ответ: 960 рублей
Cлайд 11
№8. Сколько рулонов обоев (0,5 х 10 м) потребуется для оклейки стен детской комнаты, размеры которой 4 х 2,5 м. Высота комнаты 2,5 м. Дверь имеет размеры: ширина 0,8 м, высота 1,9 м. Окно: высота 1,4 м; ширина 1,55 м. Решение. 0,8 · 1,9 = 1,52 (м2) – площадь двери; 1,4 · 1,55 = 2,17 (м2) – площадь окна; 1,52 + 2,17 = 4,34 (м2) – площадь двери и окна; (4+2,5) · 2 · 2,5 = 6,5 · 5 = 32,5 (м2) – площадь стен; 32,5 – 4,34 = 28,16 (м2) – площадь для оклеивания; 0,5 · 10 = 5 (м2) – площадь 1-го рулона; 28,16 : 5 = 5,632 ≈ 6 рулонов. Ответ: 6 рулонов
Cлайд 12
№9. Решено стены, пол, потолок обложить плиткой по цене 600 руб. за 1 м2. Дверь имеет размеры 0,8 х 2 м. Сколько будет стоить вся плитка, если ее надо купить с запасом в 10%. Длина комнаты 1,8 м, ширина 2 м, высота 2,5м. Решение. 1,8 · 2 · 2 = 7,2 (м2) – площадь пола и потолка; (1,8 + 2) · 2 · 2,5 = 3,8 · 5 = 19 (м2) – площадь стен; 0,8 · 2 = 1,6 (м2) – площадь двери; 7,2 + 19 – 1,6 = 24,6 (м2) – площадь для укладки плиты; 24,6 · 0,1 = 2,46 (м2) – запас; 24,6 + 2,46 = 27,06 (м2) – общая площадь плитки; 27,06 · 600 = 16236 (руб.) – стоимость всей плитки. Ответ: 16236 рублей
Cлайд 13
№10. Длина спортзала 10 м, ширина 20 м, высота 5 м. Сколько кг кислорода содержится в этом зале, если 1 м3 воздуха весит 1,3 кг, а вес кислорода составляет 0,21 веса воздуха? Решение. 10 · 20 · 5 = 1000 (м3) – объем зала; 1000 · 1,3 = 1300 (кг) – вес воздуха; 1300 · 0,21 = 273 (кг) – вес кислорода. Ответ: 273 кг.
Cлайд 14
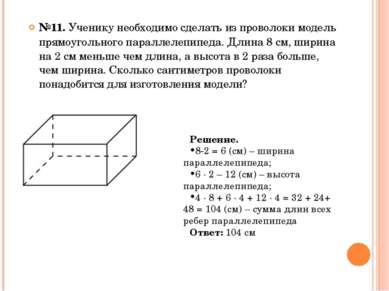№11. Ученику необходимо сделать из проволоки модель прямоугольного параллелепипеда. Длина 8 см, ширина на 2 см меньше чем длина, а высота в 2 раза больше, чем ширина. Сколько сантиметров проволоки понадобится для изготовления модели? Решение. 8-2 = 6 (см) – ширина параллелепипеда; 6 · 2 – 12 (см) – высота параллелепипеда; 4 · 8 + 6 · 4 + 12 · 4 = 32 + 24+ 48 = 104 (см) – сумма длин всех ребер параллелепипеда Ответ: 104 см
Cлайд 15
Используемая литература 1. Колягин Ю.М. и Пикан В.В. О прикладной и практической направленности обучения математике // Математика в школе. 1985. © 6. 2. Тихонов А.Н., Костомаров Д.П. Рассказы о прикладной математике. М.: Наука, 1974. 3. Шапиро И. М. Использование задач с практическим содержанием в обучении математике. М.: Просвещение, 1990. 4. http://www.math-on-line.com/olympiada-math/logic-problems.html 5. http://www.math-on-line.com/olympiada-edu/kenguru-math-56-geometria.html
Cлайд 16
Решайте задачи практического содержания с удовольствием!
