X
Код презентации скопируйте его
Задания с параметром ЕГЭ C5
Скачать эту презентацию
Презентация на тему Задания с параметром ЕГЭ C5
Скачать эту презентациюCлайд 1
Решение заданий ЕГЭ. С – 5. Муниципальное общеобразовательное бюджетное учреждение «Красномайская средняя общеобразовательная школа». Учитель первой квалификационной категории Лысак Ольга Викторовна
Cлайд 2
№1. Найдите все значения a, при каждом из которых система не имеет решений. Решение: Рассмотрим второе неравенство системы Произведение должно быть положительным. Если а = 1, то неравенство, а значит и система не имеет решений. (0 > 8) Если а < 1, то решение неравенства – луч Если а > 1, то решение неравенства – луч
Cлайд 3
При а 1 первое неравенство системы принимает вид: Или при условии
Cлайд 4
Рассмотрим решение системы в которую преобразовалось 1 неравенство. Если а < 1, то получаем: 1 а > 0. тогда знак неравенства зависит от знаков 2 и 3 множителей. Из которых получаем: Решением системы в этом случае получаем:
Cлайд 5
Если а > 1, то получаем: 1 а < 0, значит произведение 2 и 3 множителей должно быть отрицательным. Решение в этом случае – полуинтервал : Отметим, что .
Cлайд 6
Для того , чтобы система не имела решений, при а 1, необходимо и достаточно найти решение системы неравенств. Ответ:
Cлайд 7
№ 2. Найти все значения а, при каждом из которых график функции пересекает ось абсцисс более чем в двух различных точках. Решение. Рассмотрим вспомогательную функцию . График функции f(x) пересекает ось абсцисс в трёх или более точках, если уравнение g(x) = а имеет более двух различных корней. Построим график функции g(x) .
Cлайд 8
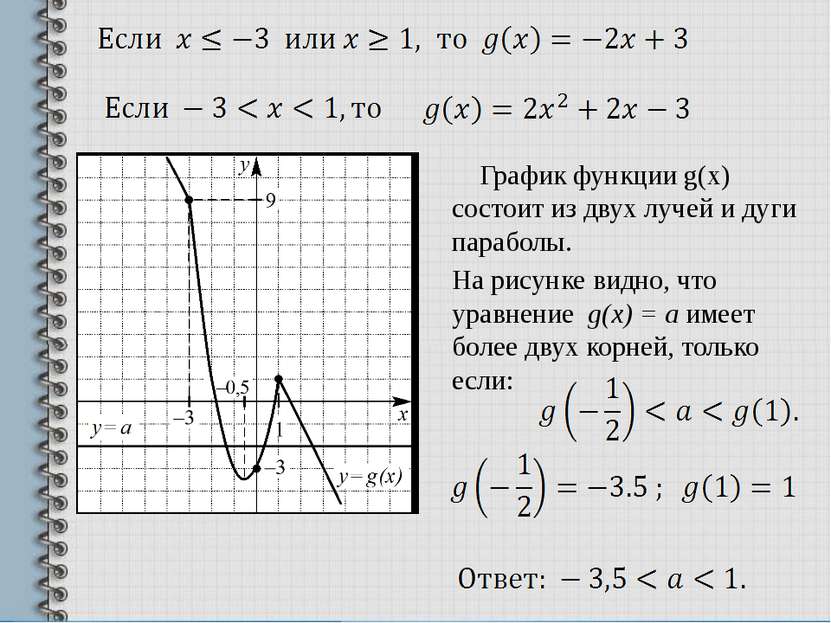
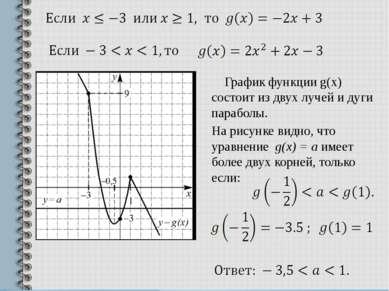График функции g(x) состоит из двух лучей и дуги параболы. На рисунке видно, что уравнение g(x) = а имеет более двух корней, только если:
Cлайд 9
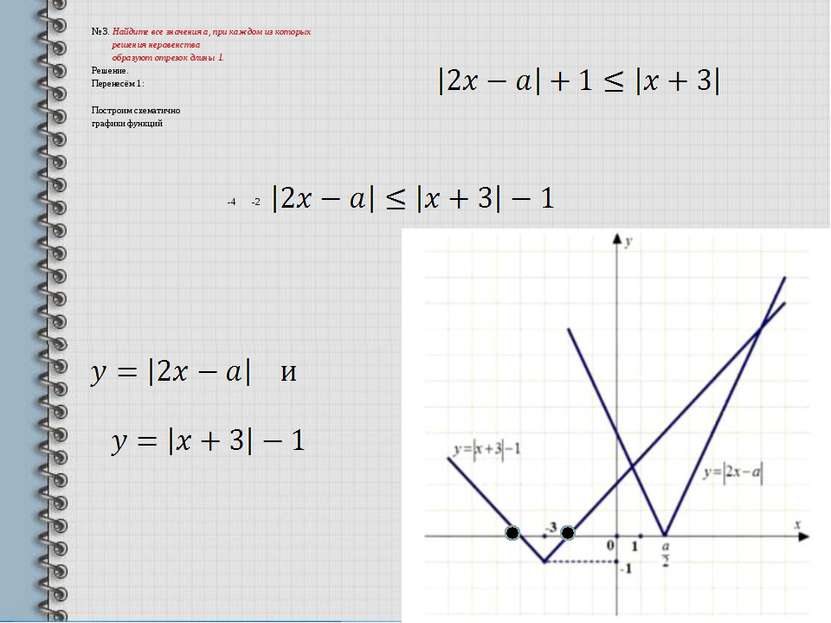
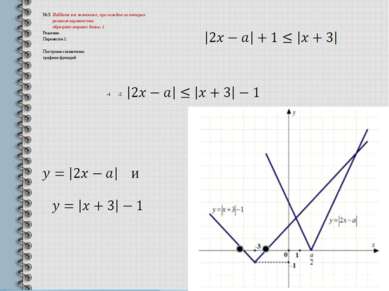№ 3. Найдите все значения а, при каждом из которых решения неравенства образуют отрезок длины 1. Решение. Перенесём 1: Построим схематично графики функций -4 -2
Cлайд 10
На рисунке видно, что неравенство имеет решения только при . 1 случай Решения образуют отрезок длины 1, если
Cлайд 11
Ответ: а = 9,5; а = 2,5 2 случай Решения образуют отрезок длины 1, если
