X
Код презентации скопируйте его
Сумма (разность) функций
Скачать эту презентацию
Презентация на тему Сумма (разность) функций
Скачать эту презентациюCлайд 1
Сумма (разность) функций
Cлайд 2
Содержание Определение Алгоритм построения (сумма функций) Пример №1 Алгоритм построения (разность функций) Пример №2 Выполнить построение Выход
Cлайд 3
Сумма функций Суммой функций ƒ(x) и g(x) называется функция h(x) с областью определения, являющейся общей частью областей определения ƒ(x) и g(x), при этом значении функции h(x) равны ƒ(x) + g(x).
Cлайд 4
Построение графика функции h(x)= ƒ(x) + g(x): Построить график функции y=ƒ(x) В той же системе координат построить график функци y=g(x) В каждой точке к отрезку изображающему ординату первого графика, пристроить отрезок, изображающий ординату второго графика.
Cлайд 5
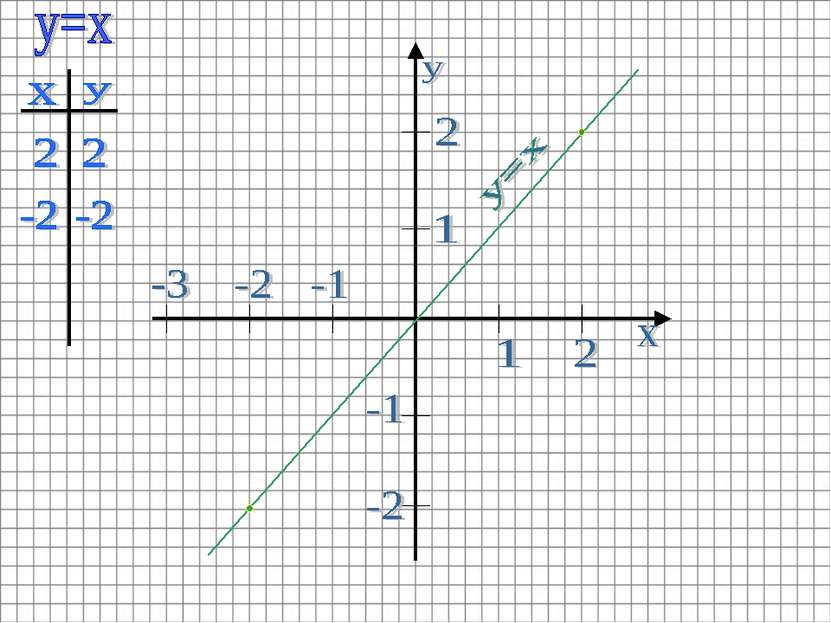
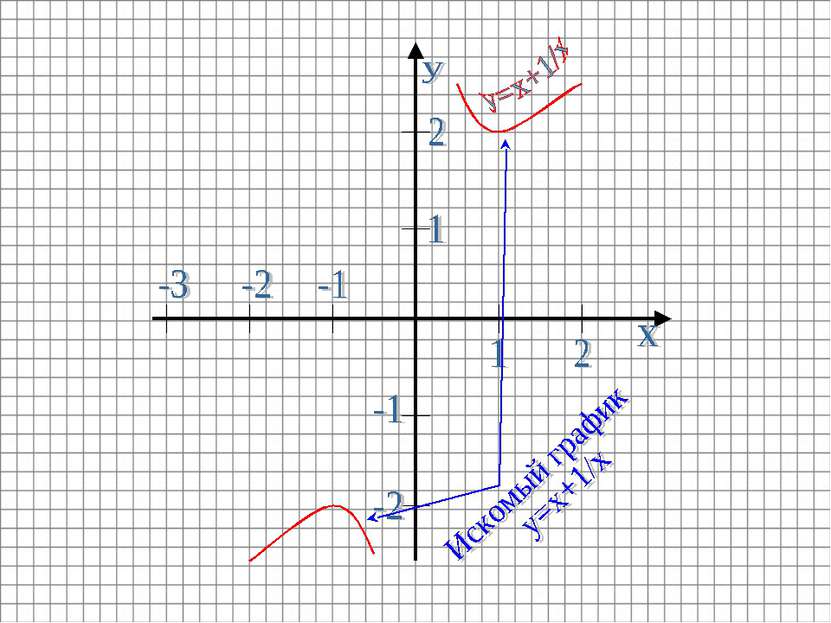
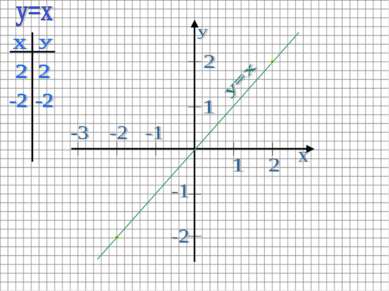
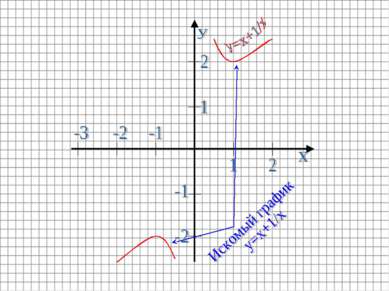
Пример: Построить график функции y=x+1/x Строим график функции y=x Графиком этой функции является прямая. Биссектриса I и III координатных углов.
Cлайд 6
Cлайд 7
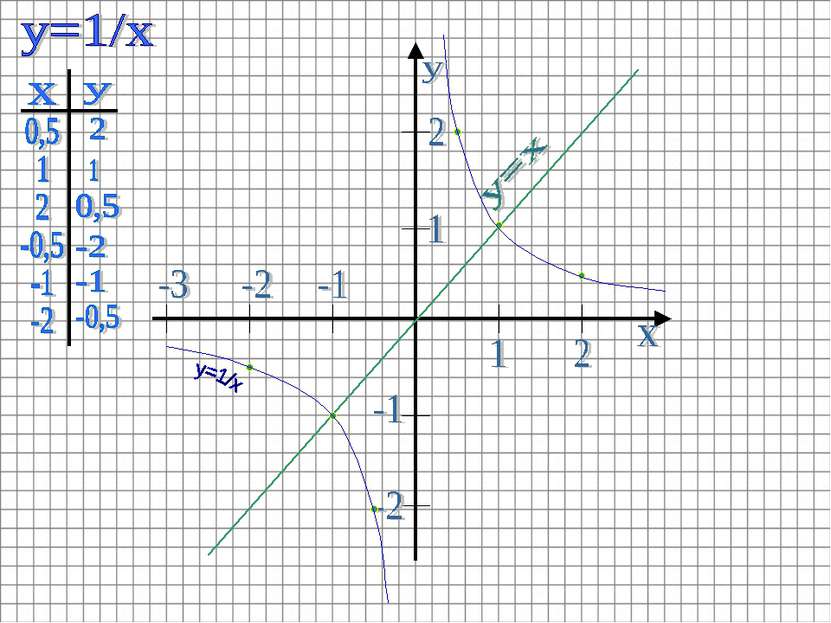
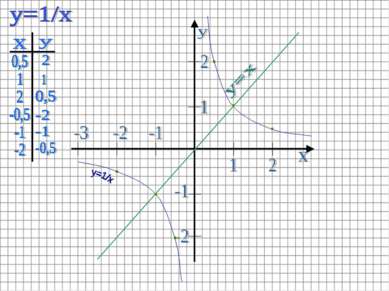
В той же системе координат строим график функции y=1/x. Графиком этой функции является гипербола, располагающаяся в I и III координатных четвертях.
Cлайд 8
Cлайд 9
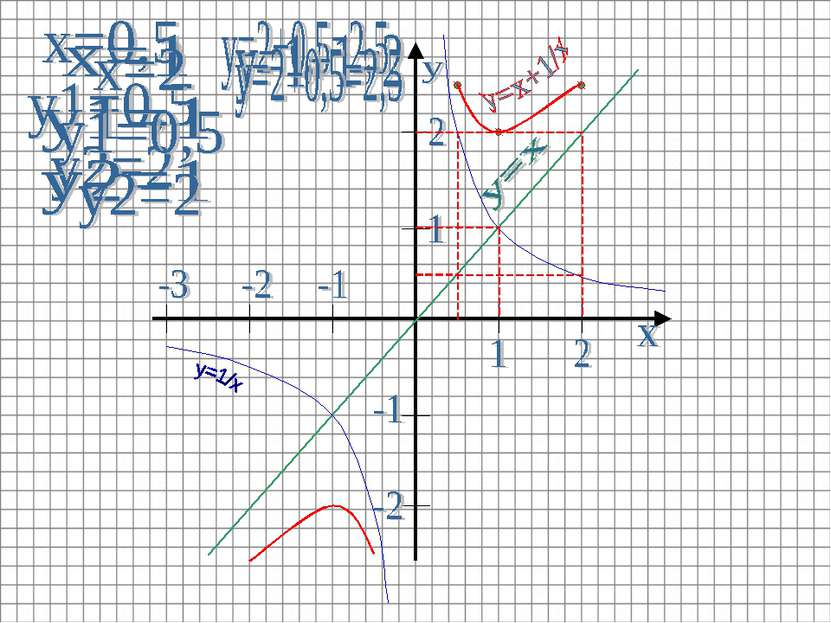
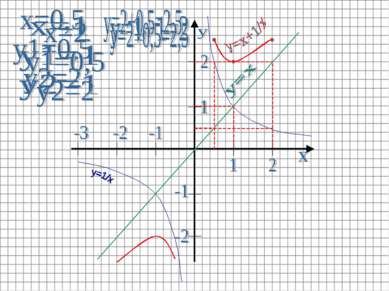
Для каждого значения x (x≠0) складываем длины соответствующих отрезков, изображающих ординаты.
Cлайд 10
Cлайд 11
Cлайд 12
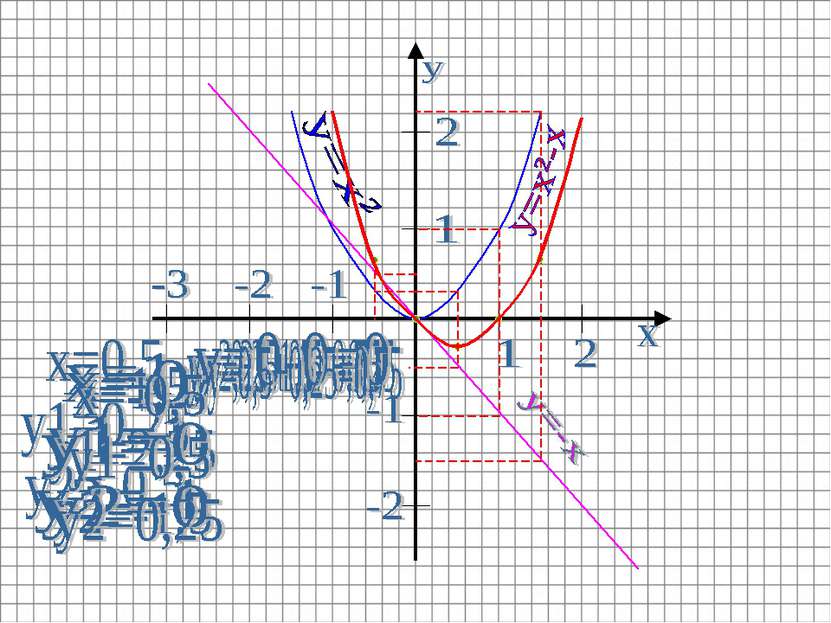
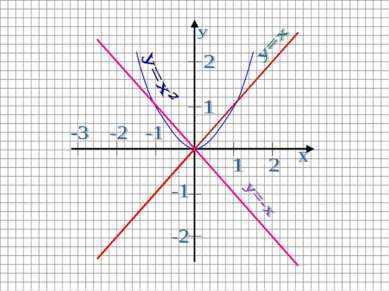
Построение графика функции h(x)=ƒ(x) - g(x) Аналогично сумме, определяется разность двух функций и строится её график. При построении графика разности можно поступить иначе: Строим график функции y=ƒ(x) В этой же системе координат строим график функции y=g(x) График функции y=g(x) отобразить симметрично относительно оси 0x. (тем самым получится график функции y=-g(x)) Сложим графики функций y=ƒ(x) и y=g(x).
Cлайд 13
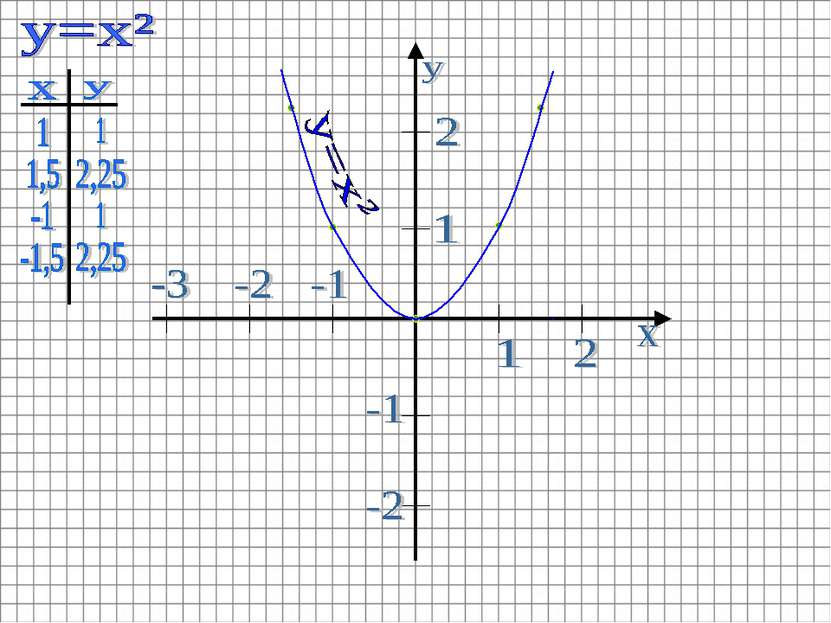
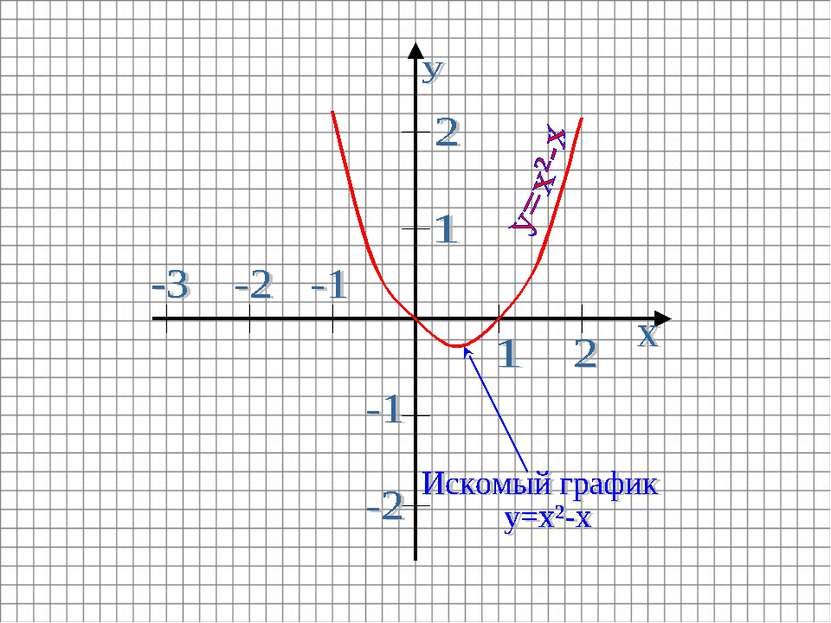
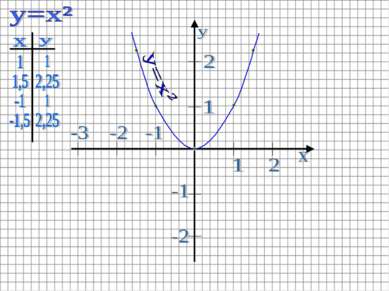
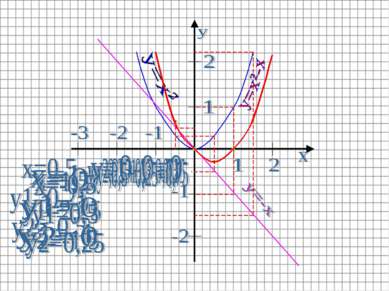
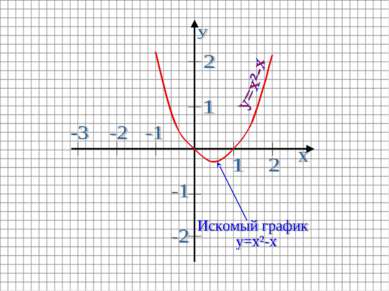
Построить график функции y=x²-x Строим график функции y=x² Графиком этой функции является парабола Ветви направлены вверх (т.к. a=1>0) Вершина находится в точке O(0;0). Пример 2:
Cлайд 14
Cлайд 15
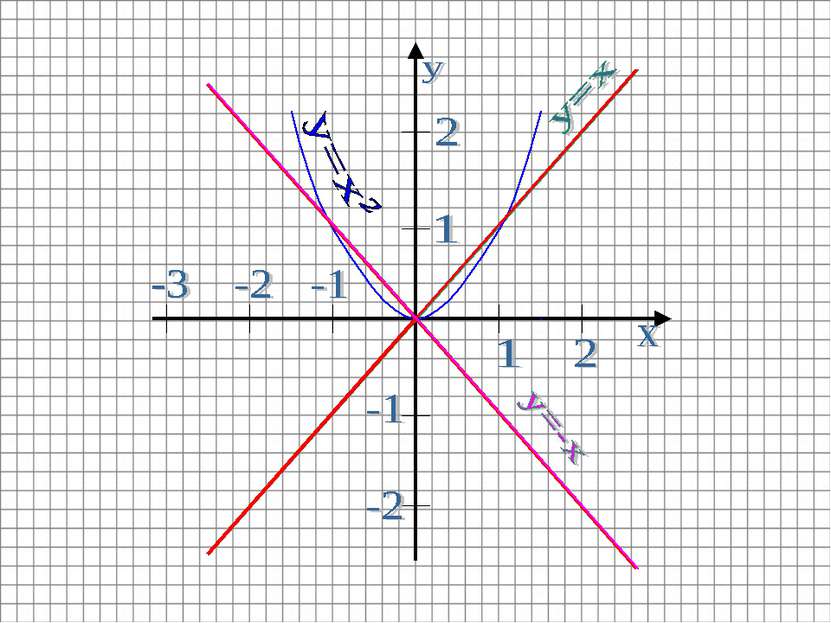
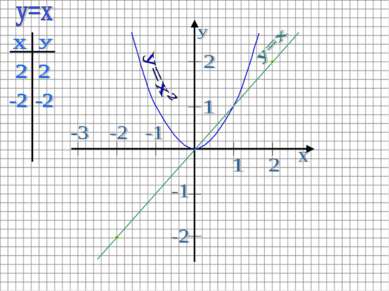
Строим график функции y=x в той же системе координат Графиком этой функции является прямая. Биссектриса I и III координатных углов.
Cлайд 16
Cлайд 17
Симметрично отображаем график функции y=x относительно 0x (в той же системе координат). Теперь графиком этой функции будет являться прямая, проходящая через II и IV координатные углы.
Cлайд 18
Cлайд 19
Для каждого значения x складываем соответствующие длины отрезков, изображающие ординаты.
Cлайд 20
Cлайд 21
Cлайд 22
Задание Построить графики функций y=x²+x y=1/x-(x+3) y=1/x+(x-2)
