X
Код презентации скопируйте его
Построение графиков функций сложных функций на основе свойств монотонности
Скачать эту презентацию
Презентация на тему Построение графиков функций сложных функций на основе свойств монотонности
Скачать эту презентациюCлайд 1
АВТОР проекта: Зародов Никита Евгеньевич, ученик 10-А класса МОУ «СОШ №21», г. Подольск, МО РУКОВОДИТЕЛЬ проекта: Буянова Анна Матвеевна, учитель математики МОУ «СОШ №21», г. Подольск, МО «ПОСТРОЕНИЕ ГРАФИКОВ СЛОЖНЫХ ФУНКЦИЙ на основе свойств монотонности»
Cлайд 2
Графики сложных функций вида y=f (v (x)) легко построить, зная свойства основных элементарных функций вида y=f (x).
Cлайд 3
ДЛЯ ЭТОГО ВСПОМНИМ
Cлайд 4
Cлайд 5
Cлайд 6
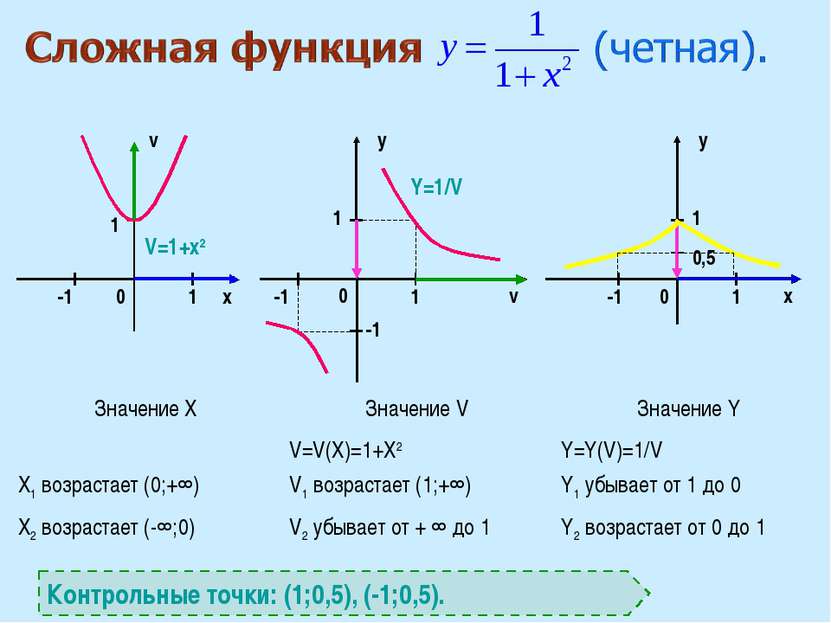
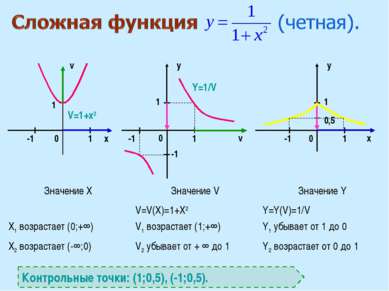x v v x y y 0 0 0 1 1 1 1 1 0,5 -1 -1 1 V=1+х2 Y=1/V Контрольные точки: (1;0,5), (-1;0,5). -1 -1 Значение X Значение V Значение Y X1 возрастает (0;+∞) V=V(X)=1+X2 V1 возрастает (1;+∞) Y=Y(V)=1/V Y1 убывает от 1 до 0 X2 возрастает (-∞;0) V2 убывает от + ∞ до 1 Y2 возрастает от 0 до 1
Cлайд 7
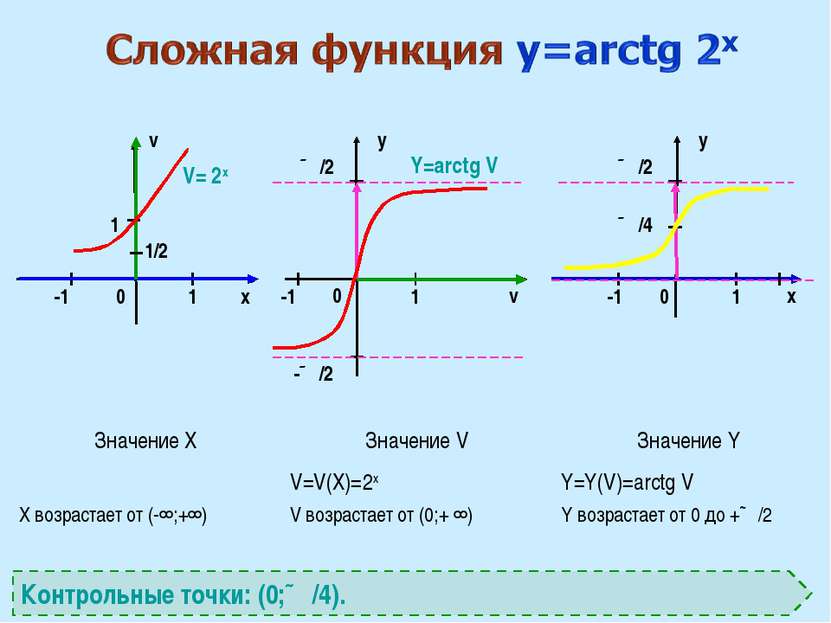
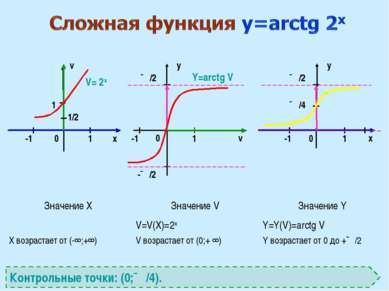x v v x y y 0 0 0 1 1 1 ∏/2 -1 1 V= 2x Y=arctg V Контрольные точки: (0;∏/4). ∏/2 -1 -∏/2 ∏/4 1/2 -1 Значение X Значение V Значение Y X возрастает от (-∞;+∞) V=V(X)=2x V возрастает от (0;+ ∞) Y=Y(V)=arctg V Y возрастает от 0 до +∏/2
Cлайд 8
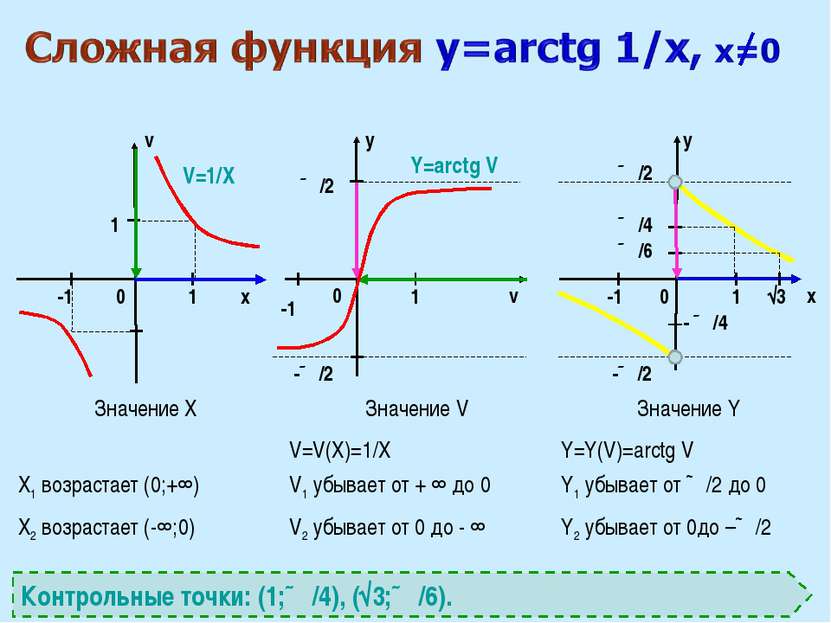
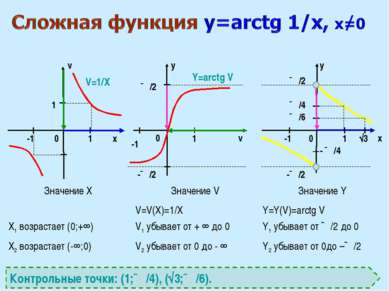x v v x y y 0 0 0 1 1 1 ∏/2 √3 -1 -1 1 V=1/X Y=arctg V Контрольные точки: (1;∏/4), (√3;∏/6). ∏/2 -1 -∏/2 -∏/2 ∏/4 - ∏/4 ∏/6 Значение X Значение V Значение Y X1 возрастает (0;+∞) V=V(X)=1/X V1 убывает от + ∞ до 0 Y=Y(V)=arctg V Y1 убывает от ∏/2 до 0 X2 возрастает (-∞;0) V2 убывает от 0 до - ∞ Y2 убывает от 0до –∏/2
Cлайд 9
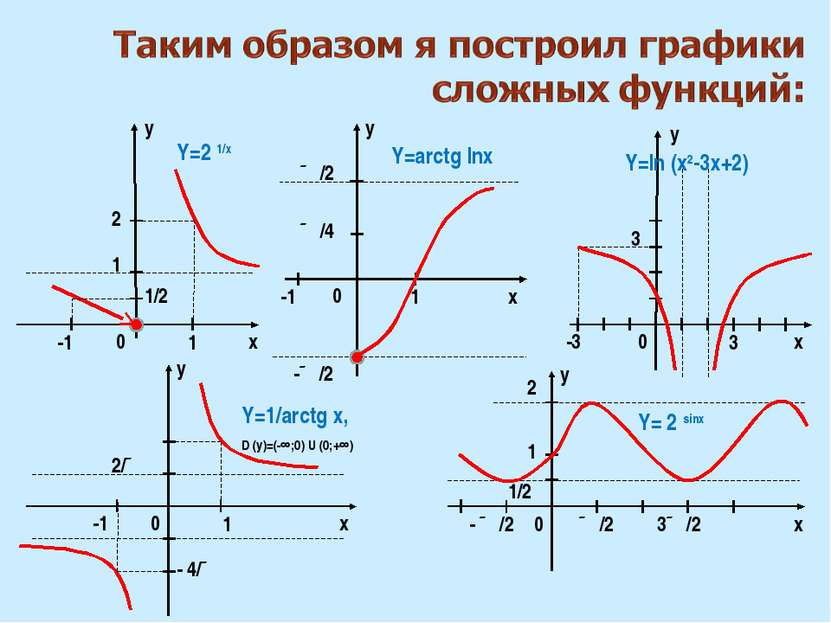
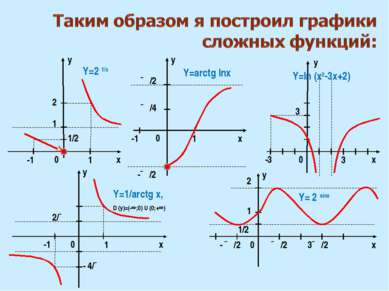x x y 0 0 0 1 1 ∏/2 -1 1 Y=2 1/х Y=arctg lnх 1/2 -1 -∏/2 ∏/2 ∏/4 - ∏/2 3∏/2 y x 2 1/2 -3 3 3 Y=ln (x2-3х+2) x y 0 1 -1 2/∏ - 4/∏ Y=1/arctg х, D (y)=(-∞;0) U (0;+∞) y y 2 1 0 x Y= 2 sinх
Cлайд 10
1. начертить графики внутренней v = v(x) и внешней y = f (v) функций и систему координат XOY. 6. построить график сложной функции y = y (x) в системе координат XOY с учетом промежутков монотонности Х, Y и контрольных точек. 2. определить промежутки монотонности внутренней функции v = v (x). 4. на каждом промежутке определить границы изменения функции v = v(x) и выбрать те значения v (x), которые попадают в область определения функции y = f (v). 3. определить промежутки монотонности внешней функции y = f(v). 5. по графику внешней функции y = f (v) найти характер изменения функции y. И ВЫРАБОТАЛ
Cлайд 11
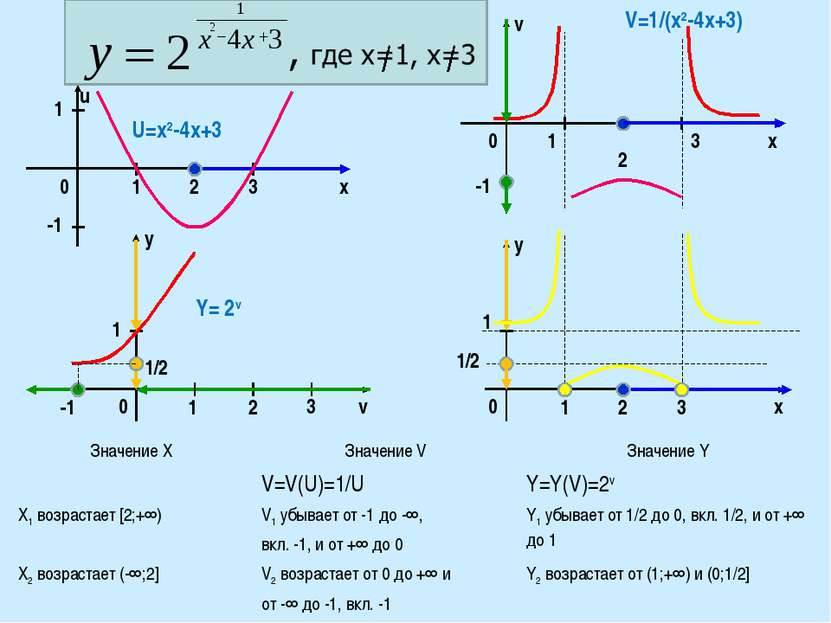
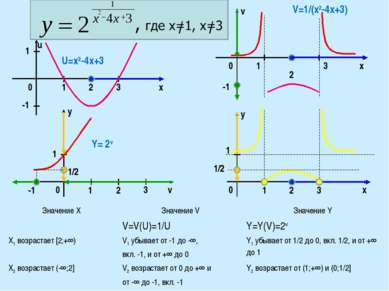0 0 1 3 1 -1 1 1/2 2 3 2 -1 x 1 Y= 2v y y 1/2 v 0 x 1 2 3 1 u 0 v U=x2-4x+3 -1 x V=1/(x2-4x+3) 1 2 3 Значение X Значение V Значение Y X1 возрастает [2;+∞) V=V(U)=1/U V1 убывает от -1 до -∞, вкл. -1, и от +∞ до 0 Y=Y(V)=2v Y1 убывает от 1/2 до 0, вкл. 1/2, и от +∞ до 1 X2 возрастает (-∞;2] V2 возрастает от 0 до +∞ и от -∞ до -1, вкл. -1 Y2 возрастает от (1;+∞) и (0;1/2]
Cлайд 12
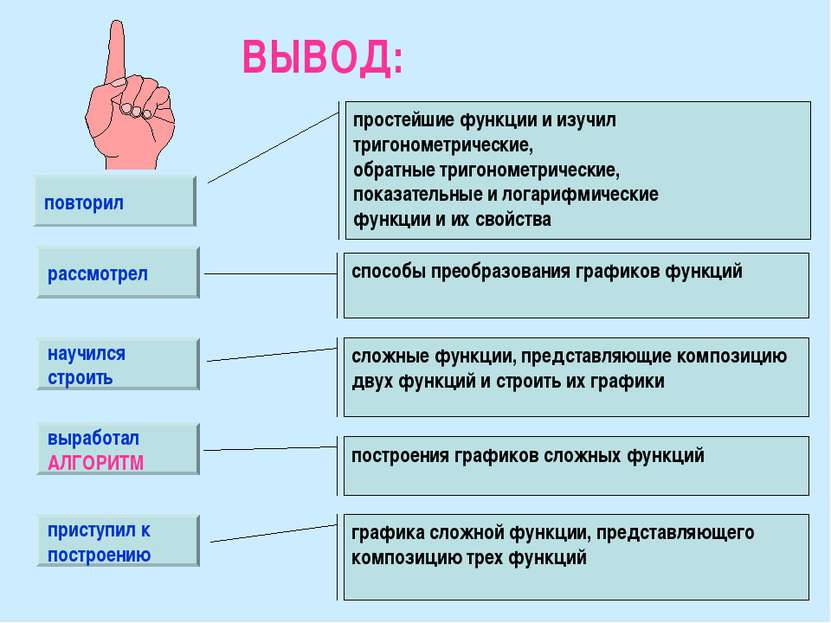
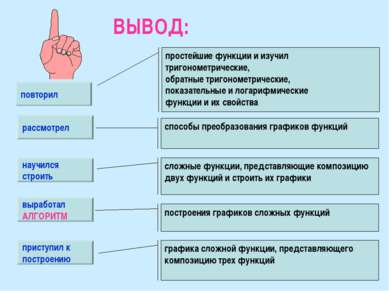ВЫВОД: повторил рассмотрел простейшие функции и изучил тригонометрические, обратные тригонометрические, показательные и логарифмические функции и их свойства способы преобразования графиков функций научился строить сложные функции, представляющие композицию двух функций и строить их графики выработал АЛГОРИТМ приступил к построению построения графиков сложных функций графика сложной функции, представляющего композицию трех функций
