X
Код презентации скопируйте его
Интегралы
Скачать эту презентациюПрезентация на тему Интегралы
Скачать эту презентациюCлайд 2
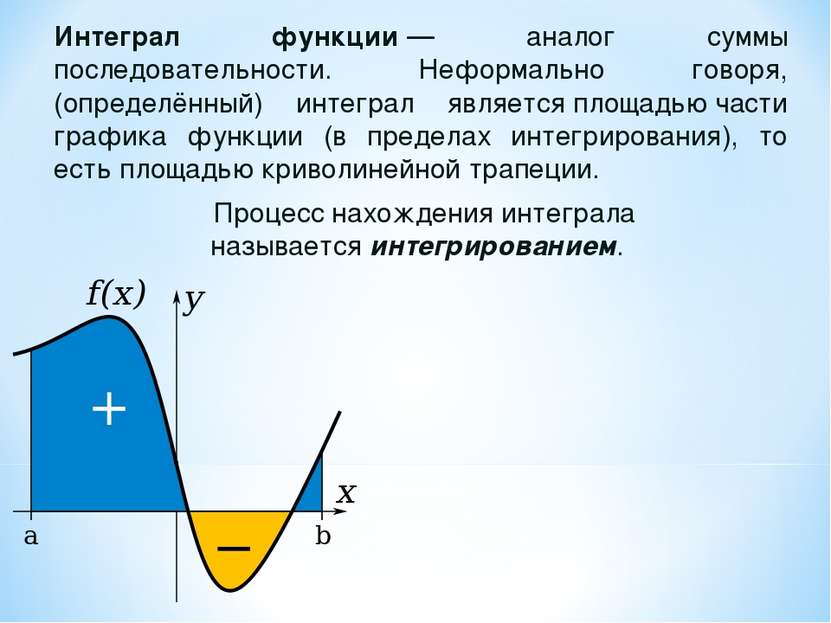
 Интеграл функции — аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика функции (в пределах интегрирования), то есть площадью криволинейной трапеции. Процесс нахождения интеграла называется интегрированием.
Интеграл функции — аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика функции (в пределах интегрирования), то есть площадью криволинейной трапеции. Процесс нахождения интеграла называется интегрированием.
Cлайд 3
 Согласно основной теореме анализа, интегрирование является операцией, обратной дифференцированию, чем помогает решать дифференциальные уравнения. Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат. Наиболее простым является интеграл Римана.
Согласно основной теореме анализа, интегрирование является операцией, обратной дифференцированию, чем помогает решать дифференциальные уравнения. Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат. Наиболее простым является интеграл Римана.
Cлайд 4
 Интегрирование прослеживается еще в древнем Египте, примерно в 1800 г. до н.э, Московский математический папирус демонстрирует знание формулы объёма усеченной пирамиды.
Интегрирование прослеживается еще в древнем Египте, примерно в 1800 г. до н.э, Московский математический папирус демонстрирует знание формулы объёма усеченной пирамиды.
Cлайд 5
 Первым известным методом для расчета интегралов является метод исчерпывания Евдокса (примерно 370 до н.э.), который пытался найти площади и объемы, разрывая их на бесконечное множество частей, для которых площадь или объем уже известны.
Первым известным методом для расчета интегралов является метод исчерпывания Евдокса (примерно 370 до н.э.), который пытался найти площади и объемы, разрывая их на бесконечное множество частей, для которых площадь или объем уже известны.
Cлайд 6
 Этот метод был подхвачен и развит Архимедом, и использовался для расчета площадей, парабол и приближенного расчета площади круга. Аналогичные методы были разработаны не зависимо в Китае в 3-м веке н.э. Лю Хуэйем, который использовал их для нахождения круга.
Этот метод был подхвачен и развит Архимедом, и использовался для расчета площадей, парабол и приближенного расчета площади круга. Аналогичные методы были разработаны не зависимо в Китае в 3-м веке н.э. Лю Хуэйем, который использовал их для нахождения круга.
Cлайд 7
 Этот метод впоследствии использовали Цзу Чунжи и Цзу Гэн для нахождения объема шара Следующий крупный шаг в исследование интегралов был сделан в Ираке, в XI веке, математиком Ибн ал-Хайсаном ( известным как Alhazen в Европе), в своей работе «Об измерении параболического тела» он приходит к уравнению четвертой степени. Решая эту проблему, он проводит вычисления, равносильные вычислению определенного интеграла, чтобы найти объем параболоида. Используя математическую индукцию, он смог обобщить свои результаты для интегралов от многочленов до четвертой степени.
Этот метод впоследствии использовали Цзу Чунжи и Цзу Гэн для нахождения объема шара Следующий крупный шаг в исследование интегралов был сделан в Ираке, в XI веке, математиком Ибн ал-Хайсаном ( известным как Alhazen в Европе), в своей работе «Об измерении параболического тела» он приходит к уравнению четвертой степени. Решая эту проблему, он проводит вычисления, равносильные вычислению определенного интеграла, чтобы найти объем параболоида. Используя математическую индукцию, он смог обобщить свои результаты для интегралов от многочленов до четвертой степени.