X
Код презентации скопируйте его
Кратные и Двойные интегралы
Скачать эту презентацию
Презентация на тему Кратные и Двойные интегралы
Скачать эту презентациюCлайд 1
Кратные интегралы Как известно, интегрирование является процессом суммирования. Однако суммирование может производится неоднократно, что приводит нас к понятию кратных интегралов. Рассмотрение этого вопроса начнем с рассмотрения двойных интегралов.
Cлайд 2
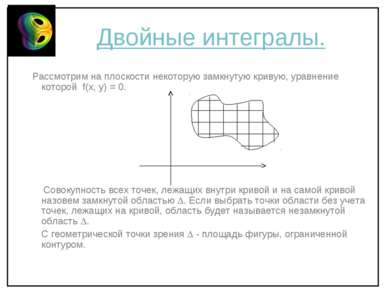Двойные интегралы. Рассмотрим на плоскости некоторую замкнутую кривую, уравнение которой f(x, y) = 0. Совокупность всех точек, лежащих внутри кривой и на самой кривой назовем замкнутой областью . Если выбрать точки области без учета точек, лежащих на кривой, область будет называется незамкнутой область . С геометрической точки зрения - площадь фигуры, ограниченной контуром.
Cлайд 3
Разобьем область на n частичных областей сеткой прямых, отстоящих друг от друга по оси х на расстояние , а по оси у – на . Вообще говоря, такой порядок разбиения необязателен, возможно разбиение области на частичные участки произвольной формы и размера. Получаем, что площадь S делится на элементарные прямоугольники, площади которых равны В каждой частичной области возьмем произвольную точку и составим интегральную сумму где f – функция непрерывная и однозначная для всех точек области . Если бесконечно увеличивать количество частичных областей i, тогда, очевидно, площадь каждого частичного участка Si стремится к нулю.
Cлайд 4
Определение Если при стремлении к нулю шага разбиения области интегральные суммы имеют конечный предел, то этот предел называется двойным интегралом от функции f(x, y) по области . учетом того, что получаем: В приведенной выше записи имеются два знака , т.к. суммирование производится по двум переменным х и у. Т.к. деление области интегрирования произвольно, также произволен и выбор точек , то, считая все площади одинаковыми, получаем формулу:
Cлайд 5
Условия существования двойного интеграла Сформулируем достаточные условия существования двойного интеграла Теорема. Если функция f(x, y) непрерывна в замкнутой области , то двойной интеграл существует.
Cлайд 6
Теорема Если функция f(x, y) ограничена в замкнутой области и непрерывна в ней всюду, кроме конечного числа кусочно – гладких линий, то двойной интеграл существует.
Cлайд 7
Свойства двойного интеграла. 1) 2) 3) Если = 1 + 2, то 4) Теорема о среднем. Двойной интеграл от функции f(x, y) равен произведению значения этой функции в некоторой точке области интегрирования на площадь области интегрирования. 5) Если f(x, y) 0 в области , то 6) Если f1(x, y) f2(x, y), то 7)
Cлайд 8
Вычисление двойного интеграла Теорема Если функция f(x, y) непрерывна в замкнутой области , ограниченной линиями х = a, x = b, (a < b), y = (x), y = (x), где и - непрерывные функции и , тогда
Cлайд 9
Теорема. Если функция f(x, y) непрерывна в замкнутой области , ограниченной линиями y = c, y = d (c < d), x = (y), x = (y) ( (y) (y)), то
Cлайд 10
Замена переменных в двойном интеграле Расмотрим двойной интеграл вида , где переменная изменяется в пределах от a до b, а переменная – от до Положим Тогда ; ; dy = ;
Cлайд 11
т.к. при первом интегрировании переменная принимается за постоянную, то подставляя это выражение в записанное выше соотношение для , получаем:
Cлайд 12
Выражение называется определителем Якоби или Якобианом функций и (Якоби Карл Густав Якоб – (1804-1851) – немецкий математик) Тогда Т.к. при первом интегрировании приведенное выше выражение для принимает вид ( при первом интегрировании полагаем ), то при изменении порядка интегрирования, получаем соотношение:
Cлайд 13
Двойной интеграл в полярных координатах. Воспользуемся формулой замены переменных: При этом известно, что В этом случае Якобиан имеет вид: Тогда Здесь - новая область значений,
