X
Код презентации скопируйте его
Движения в пространстве
Скачать эту презентацию
Презентация на тему Движения в пространстве
Скачать эту презентациюCлайд 1
Урок геометрии в 11 классе учителя Текутовой И.Н. Движения в пространстве Центральная симметрия Осевая симметрия Зеркальная симметрия Параллельный перенос У
Cлайд 2
Форма урока: Урок – семинар, решение проблемного вопроса Цели урока: Актуализировать личностное осмысление учащимися учебного материала «Движения в пространстве» Содействовать сознательному пониманию прикладного значения темы, развитию умения видеть в окружающей действительности изучаемые виды движений Развивать познавательный интерес к построению образов объектов при различных видах движений Способствовать грамотному усвоению темы, отработке практических навыков
Cлайд 3
Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство. Г. Вейль.
Cлайд 4
Движение пространства - это отображение пространства на себя, сохраняющее расстояние между точками.
Cлайд 5
Центральная симметрия
Cлайд 6
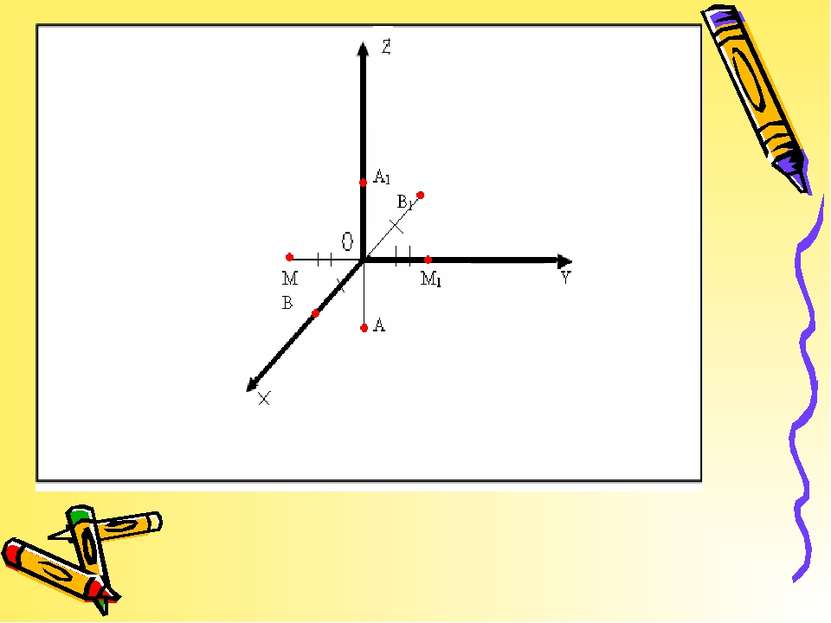
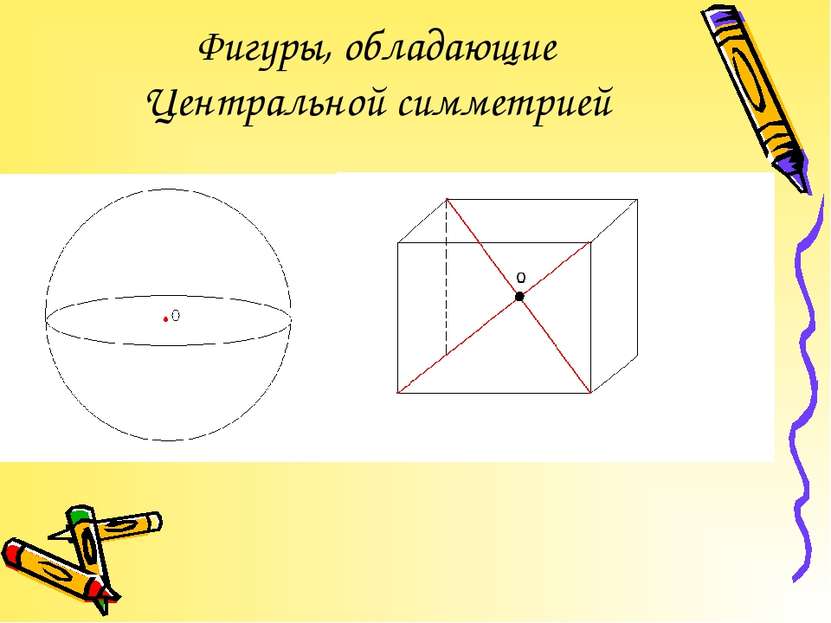
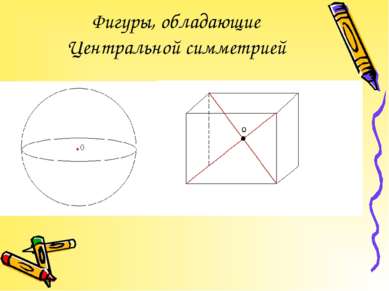
Центральная симметрия – отображение пространства на себе, при котором любая точка М переходит в симметричную ей точку М1 относительно данного центра О.
Cлайд 7
Cлайд 8
Cлайд 9
Фигуры, обладающие Центральной симметрией
Cлайд 10
Ст. метро Сокол
Cлайд 11
Ст. метро Римская
Cлайд 12
Павильон Культура, ВВЦ
Cлайд 13
.О
Cлайд 14
Осевая симметрия
Cлайд 15
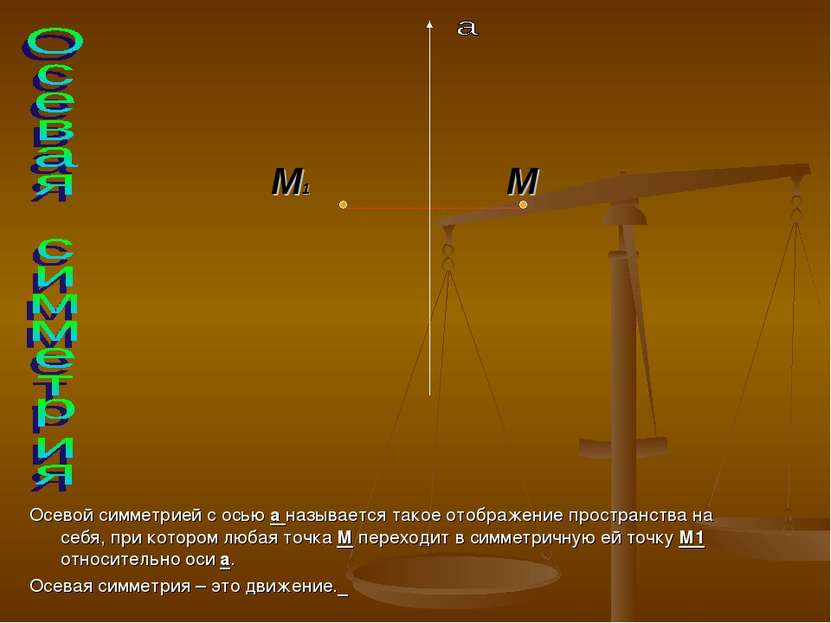
Осевой симметрией с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно оси а. Осевая симметрия – это движение. M M1
Cлайд 16
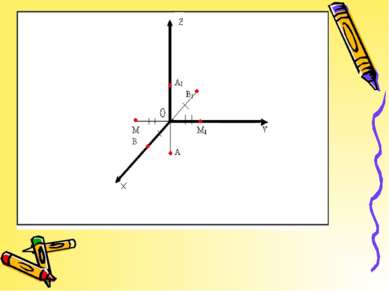
M(x;y;z) M1 (x1 ;y1;z1) Докажем, что осевая симметрия является движением. Для этого введем прямоугольную систему координат Oxyz так, чтобы ось Oz совпала с осью симметрии, и установим связь между координатами двух точек M(x;y;z) и M1(x1;y1 ;z1) симметричных относительно оси Oz. Если точка М не лежит на оси Oz, то ось Oz: 1) проходит через середину отрезка MM1 и 2) перпендикулярна к нему. Из первого условия по формулам для координат середины отрезка получаем (x+x1)/2=0 и (y+y1)/2=0, откуда x1=-x и y1=-z. Второе условие означает, что аппликаты точек M и M1 равны: z1=z.
Cлайд 17
Доказательство Рассмотрим теперь любые две точки A(x1; y1; z1) и B(x2;y2;z2) и докажем, что расстояние между симметричными им точками A1 и B1 равно AB. Точки A1 и B1 имеют координаты A1(-x1;-y1;-z1) и B1(-x1;-y1;-z1) По формуле расстояния между двумя точками находим: AB=\/(x2-x1)²+(y2-y1)²+(z2-z1), A1B1=\/(-x2+x1)²+(-y2+y1)²+(-z2+z1). Из этих соотношений ясно, что AB=A1B1, что и требовалось доказать.
Cлайд 18
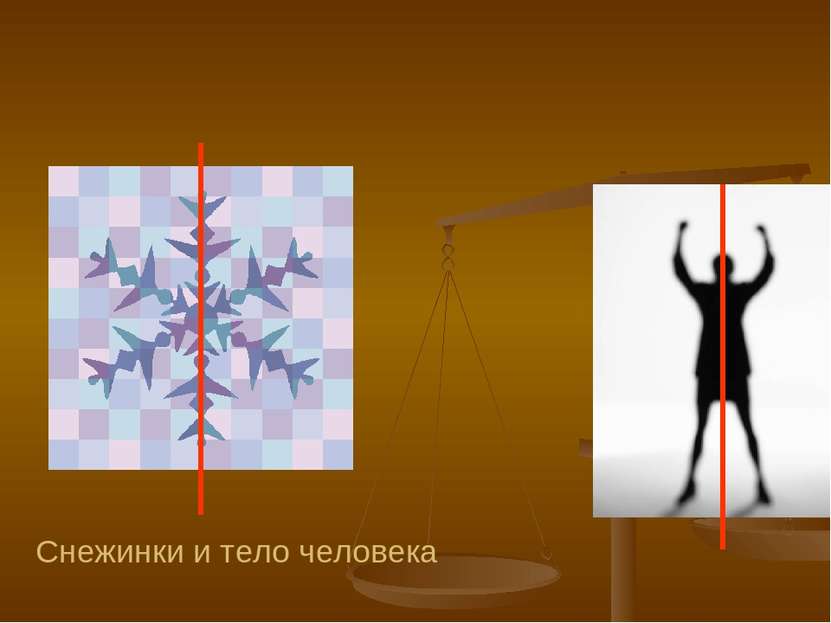
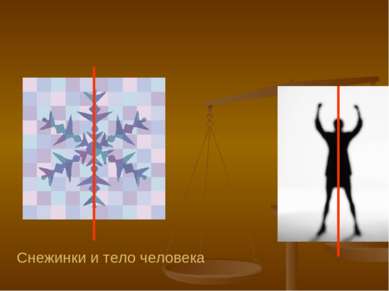
Применение Осевая симметрия встречается очень часто. Ее можно увидеть как в природе: листья растений или цветы, тело животных насекомых и даже человека, так и в творении самого человека: здания, автомобили, техника и многое другое.
Cлайд 19
Cлайд 20
Применение осевой симметрии в жизни Архитектурные строения
Cлайд 21
Снежинки и тело человека
Cлайд 22
Эйфелева Башня сова
Cлайд 23
Что может быть больше похоже на мою руку или мое ухо , чем их собственное отражение в зеркале ? И все же руку которую я вижу в зеркале , нельзя поставить на место настоящей руки. Эммануил Кант . Зеркальная симметрия
Cлайд 24
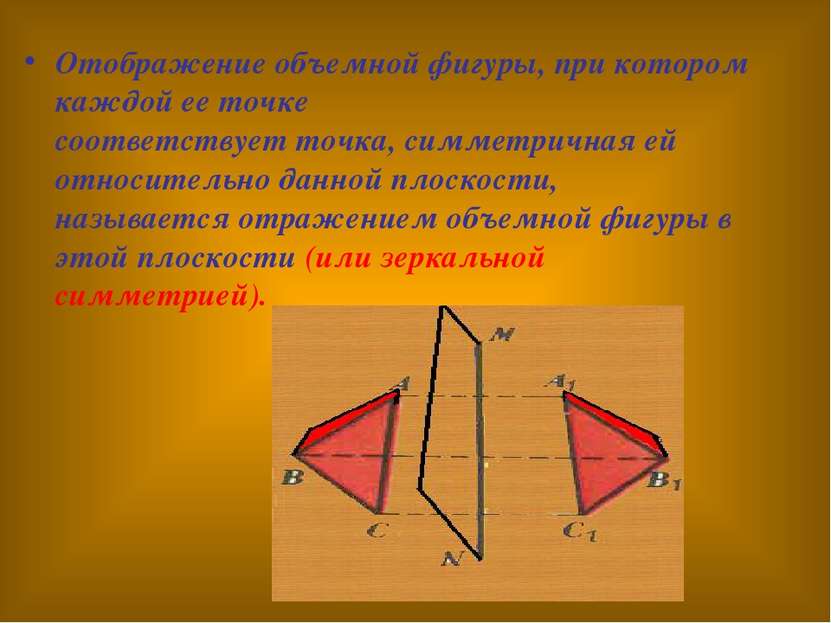
Отображение объемной фигуры, при котором каждой ее точке соответствует точка, симметричная ей относительно данной плоскости, называется отражением объемной фигуры в этой плоскости (или зеркальной симметрией).
Cлайд 25
Теорема 1. Отражение в плоскости сохраняет расстояния и, стало быть, является движением. Теорема 2. Движение, при котором все точки некоторой плоскости неподвижны, является отражением в этой плоскости или тождественным отображением. Зеркальная симметрия задается указанием одной пары соответствующих точек, не лежащих в плоскости симметрии: плоскость симметрии проходит через середину отрезка, соединяющего эти точки, перпендикулярно к нему.
Cлайд 26
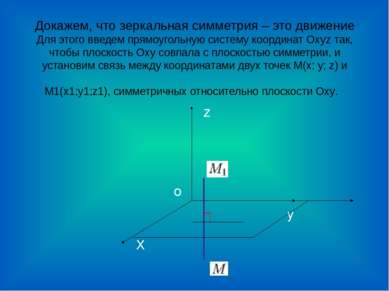Докажем, что зеркальная симметрия – это движение Для этого введем прямоугольную систему координат Оxyz так, чтобы плоскость Оxy совпала с плоскостью симметрии, и установим связь между координатами двух точек М(x; y; z) и М1(x1;y1;z1), симметричных относительно плоскости Оxy. y X z о
Cлайд 27
Если точка М не лежит в плоскости Оxy, то эта плоскость: 1) проходит через середину отрезка ММ1 и 2) перпендикулярна к нему. Из первого условия по формуле координат середины отрезка получаем (z+z1)/2=0, откуда z1=-z. Второе условие означает, что отрезок ММ1 параллелен оси Оz, и. следовательно, х1=х, у1=у. М лежит в плоскости Oxy. Рассмотрим теперь две точки А (х1;у1;z1) и В (х2;у2;z2) и докажем, что расстояние между симметричными им точками А1(х1;у1;-z1) и В (х2;у2;-z2). По формуле расстояния между двумя точками находим: АВ= корень квадратный из (х2-х1)2+(у2-у1)2+(z2-z1)2, А1В1=корень квадратный из (х2-х1)2+(у2-у1)2+(-z2-z1)2. Из этих соотношений ясно, что и требовалось доказать.
Cлайд 28
Симметрия относительно плоскости (зеркальная симметрия) пространства есть движение, а значит, обладает всеми свойствами движений: переводит прямую в прямую, плоскость --- в плоскость. Кроме того, это преобразование пространства, совпадающее со своим обратным: композиция двух симметрий относительно одной и той же плоскости есть тождественное преобразование. При симметрии относительно плоскости все точки этой плоскости, и только они, остаются на месте (неподвижные точки преобразования). Прямые, лежащие в плоскости симметрии и перпендикулярные ей, переходят в себя. Плоскости, перпендикулярные плоскости симметрии также переходят в себя. Симметрия относительно плоскости является движением второго рода (меняет ориентацию тетраэдра).
Cлайд 29
Шар симметричен относительно любой оси, проходящей через его центр.
Cлайд 30
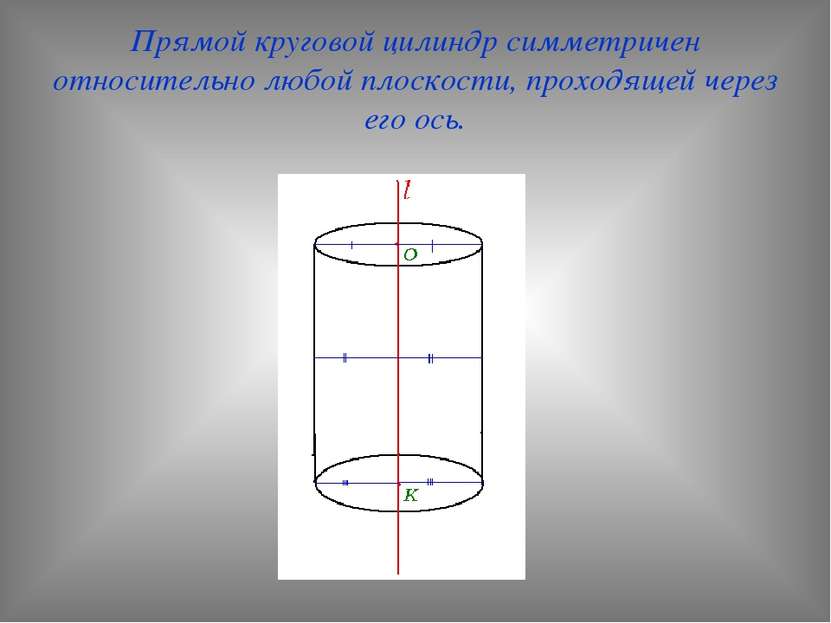
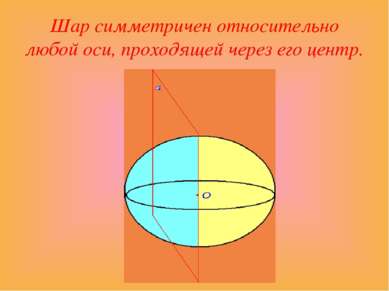
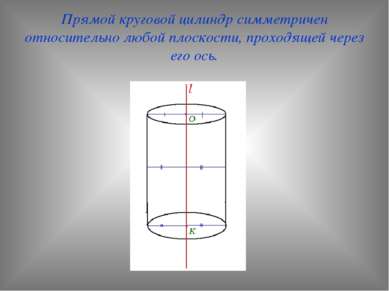Прямой круговой цилиндр симметричен относительно любой плоскости, проходящей через его ось.
Cлайд 31
Правильная n-угольная пирамида при четном n симметрична относительно любой плоскости, проходящей через ее высоту и наибольшую диагональ основания.
Cлайд 32
Обычно считают ,что наблюдаемый в зеркале двойник является точной копией самого объекта. В действительности это не совсем так . Зеркало не просто копирует объект , а меняет местами (переставляет) передние и задние по отношению к зеркалу части объекта . В сравнении с самим объектом его зеркальный двойник оказывается "вывернутым" вдоль направления перпендикулярного к плоскости зеркала .Этот эффект хорошо виден на одном рисунке и фактически незаметен на другом .
Cлайд 33
Предположим ,что одна половина объекта является зеркальным двойником по отношению к другой его половине . Такой объект называют зеркально симметричным .Он преобразуется сам в себя при отражении в соответствующей зеркальной плоскости . Эту плоскость называют плоскостью симметрии .
Cлайд 34
Здание ЕНУ им. Л.Н Гумилева
Cлайд 35
Параллельный перенос
Cлайд 36
Движение плоскости Движение плоскости – это взаимно однозначное преобразование точек плоскости при котором сохраняются расстояния: если точка А переходит в А`, В – В`, то А`В`=АВ При движении так же сохраняются углы Параллельный перенос – это отображение пространства на себя, при котором любая точка М переходит в точку М’, что MM’ = р p M M’
Cлайд 37
Cлайд 38
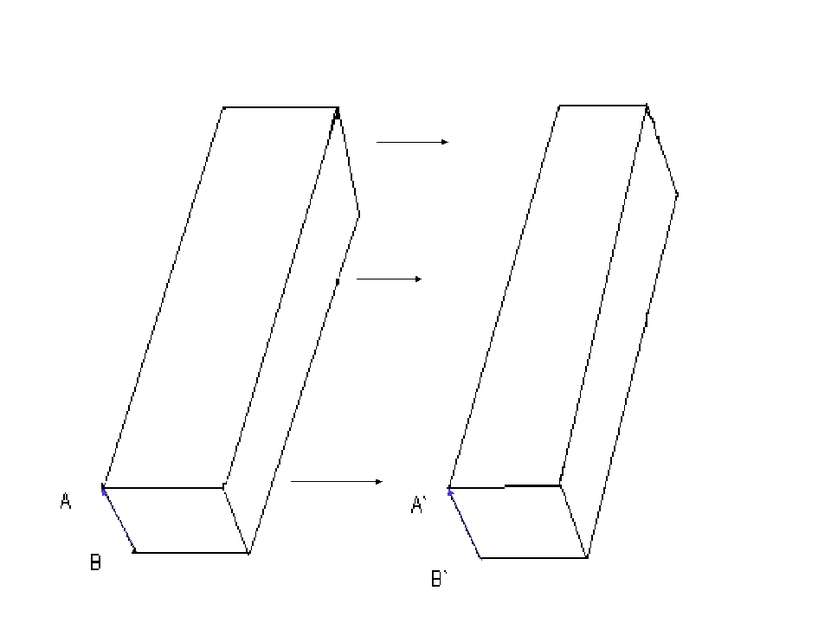
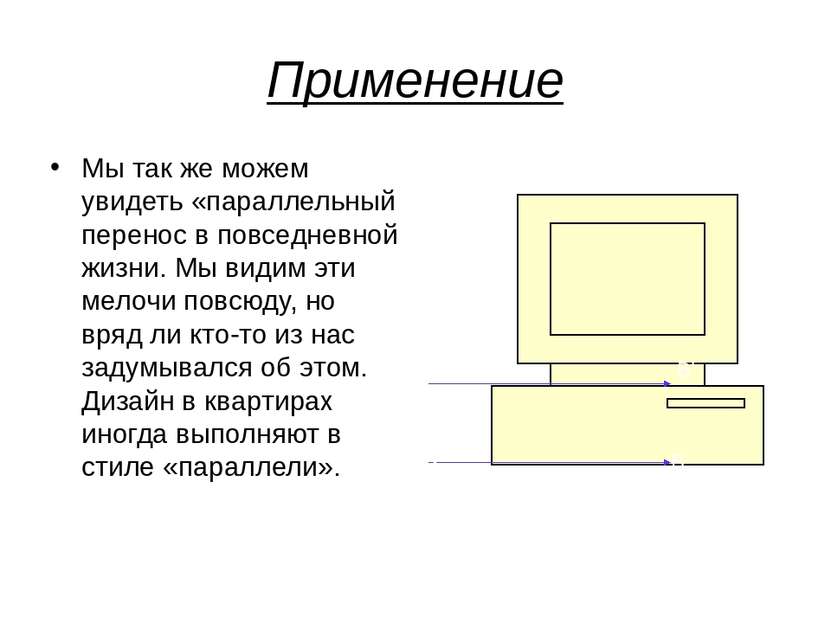
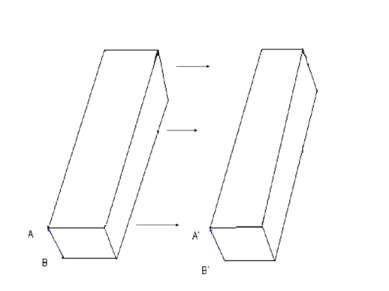
Применение Мы так же можем увидеть «параллельный перенос в повседневной жизни. Мы видим эти мелочи повсюду, но вряд ли кто-то из нас задумывался об этом. Дизайн в квартирах иногда выполняют в стиле «параллели». А В А’ В’
Cлайд 39
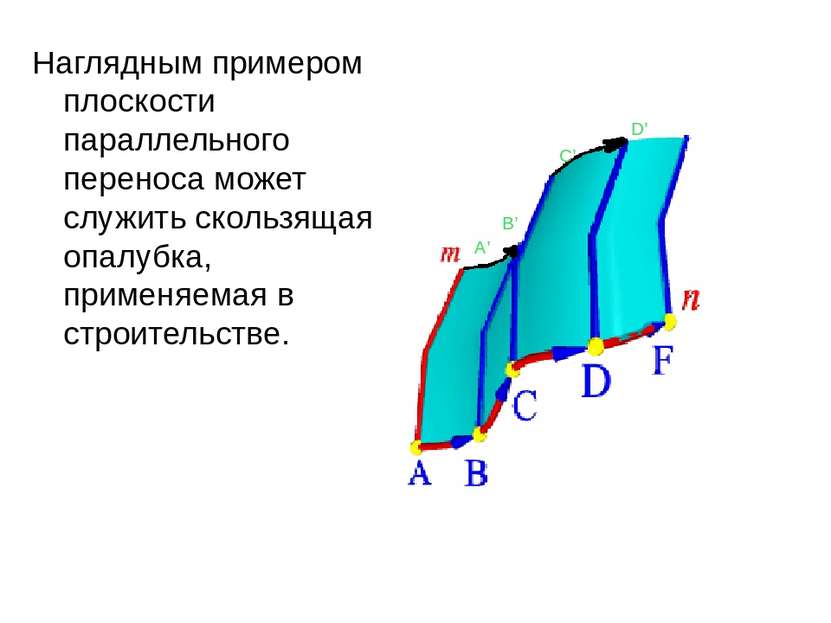
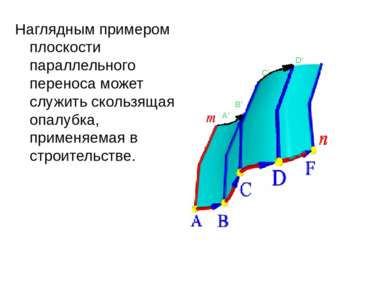
ПОВЕРХНОСТИ ПАРАЛЛЕЛЬНОГО ПЕРЕНОСА Поверхностью параллельного переноса называется поверхность, образованная поступательным плоскопараллельным перемещением образующей - плоской кривой линии m по криволинейной направляющей n
Cлайд 40
Наглядным примером плоскости параллельного переноса может служить скользящая опалубка, применяемая в строительстве. A’ B’ C’ D’
Cлайд 41
Cлайд 42
Cлайд 43
Cлайд 44
Cлайд 45
Cлайд 46
Спасибо за урок
