X
Код презентации скопируйте его
Многоугольники
Скачать эту презентацию
Презентация на тему Многоугольники
Скачать эту презентациюCлайд 1
Многоугольники МКОУ «СОШ №1 города Суздаля» Учитель математики Плотникова Т.В.
Cлайд 2
Что общего у фигур, изображённых на экране?
Cлайд 3
Нарисуйте в тетради фигуру, изображённую на экране: А1 А2 А3 А4 А5 Назовите отрезки, из которых состоит данная фигура. Их можно разделить на смежные и несмежные.
Cлайд 4
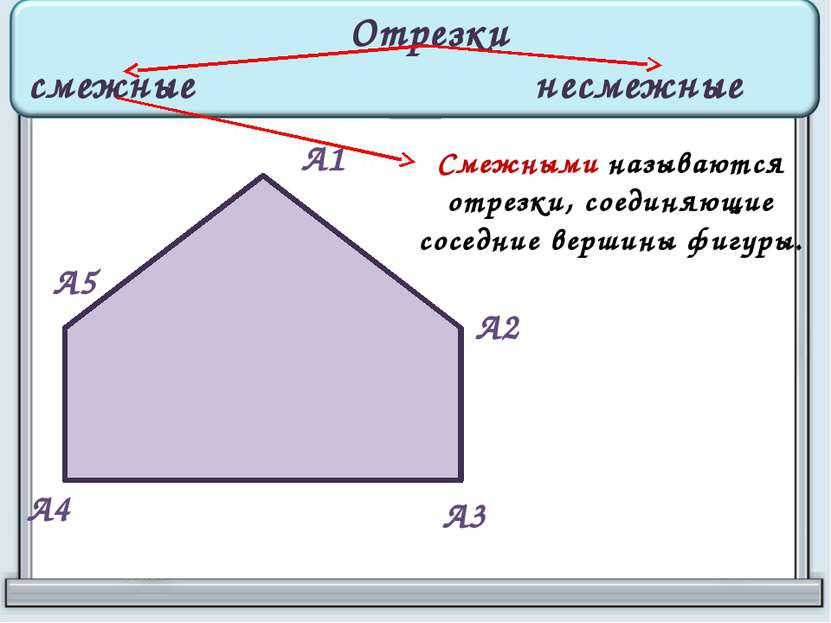
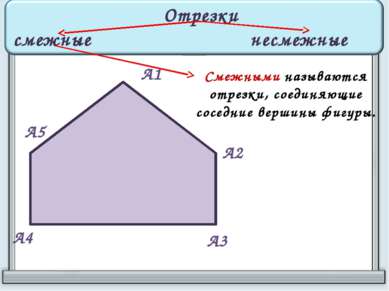А1 А2 А3 А4 А5 Смежными называются отрезки, соединяющие соседние вершины фигуры. Отрезки смежные несмежные
Cлайд 5
Многоугольник-фигура, состоящая из отрезков, причём смежные отрезки не лежат на одной прямой, а несмежные отрезки не пересекаются. Определение: А В С D Е F К Учебник: рис.150,151,152
Cлайд 6
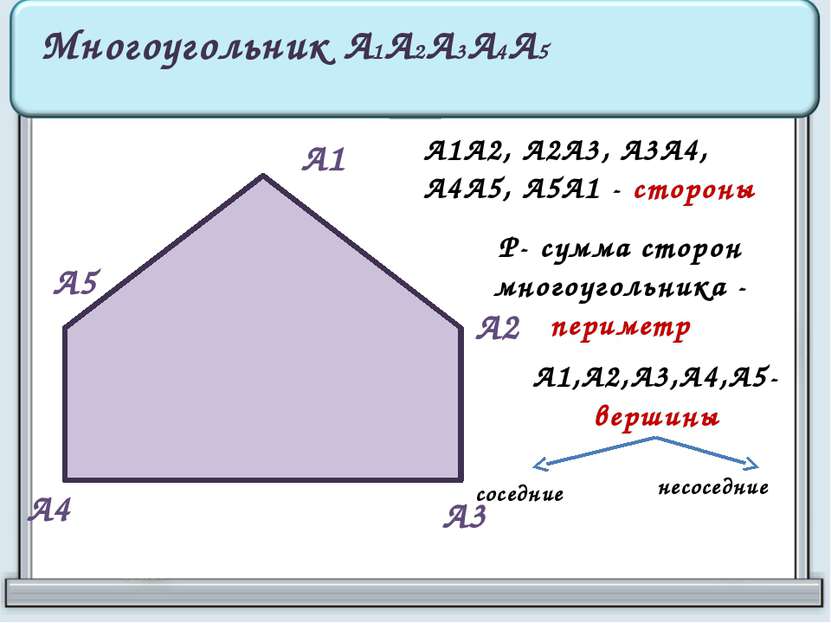
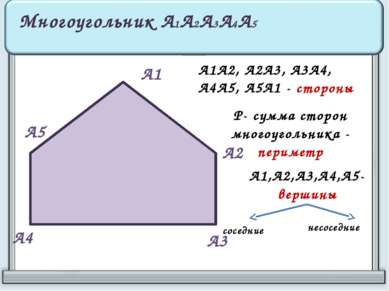А1 А2 А3 А4 А5 Многоугольник А1А2А3А4А5 А1А2, А2А3, А3А4, А4А5, А5А1 - стороны Р- сумма сторон многоугольника - периметр А1,А2,А3,А4,А5- вершины соседние несоседние
Cлайд 7
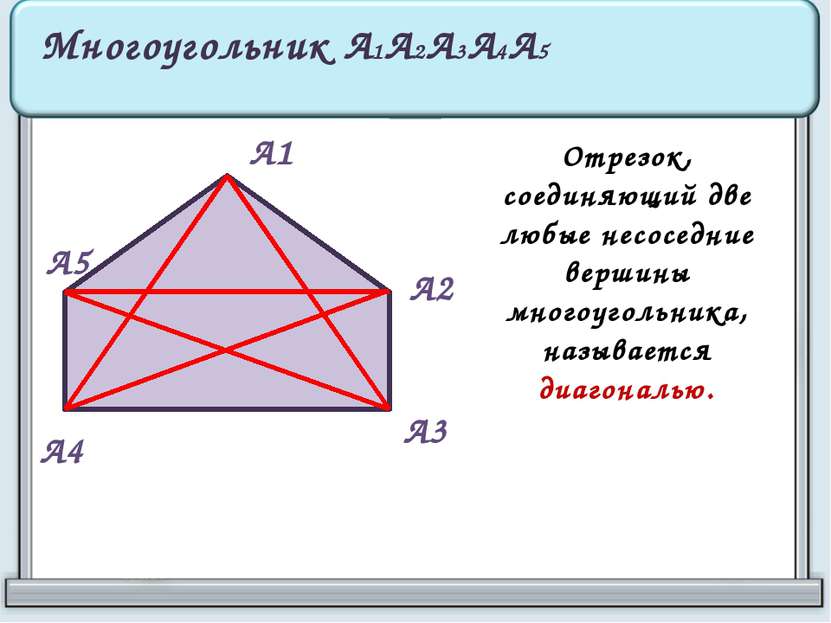
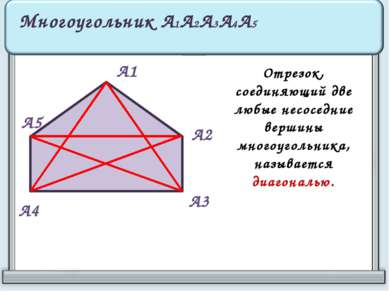А1 А2 А3 А4 А5 Многоугольник А1А2А3А4А5 Отрезок, соединяющий две любые несоседние вершины многоугольника, называется диагональю.
Cлайд 8
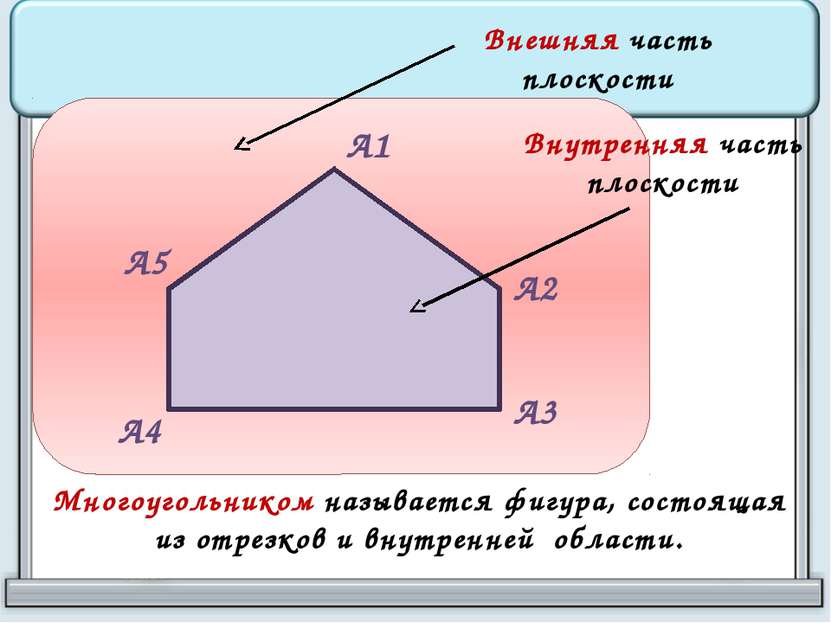
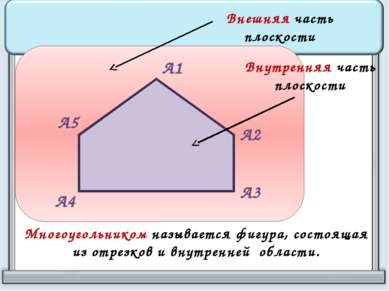А1 А2 А3 А4 А5 Внешняя часть плоскости Внутренняя часть плоскости Многоугольником называется фигура, состоящая из отрезков и внутренней области.
Cлайд 9
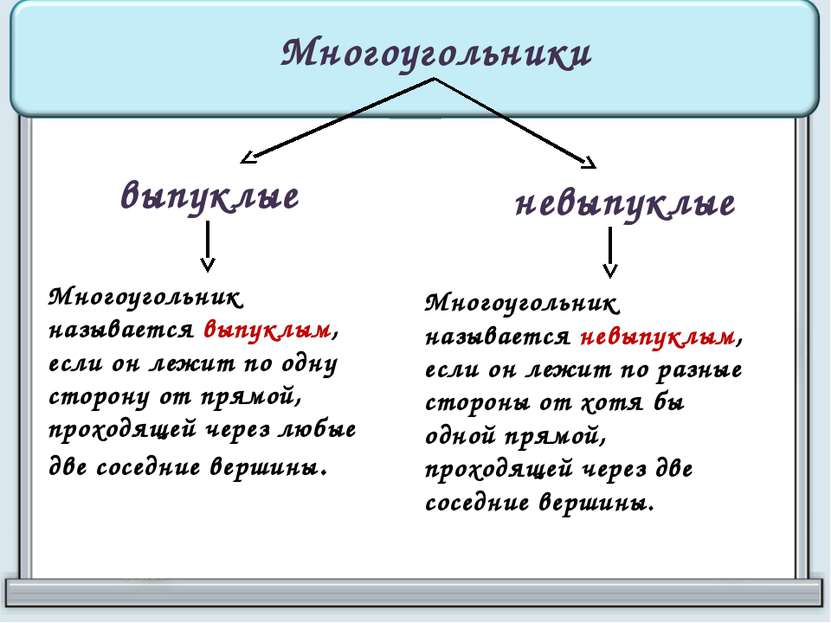
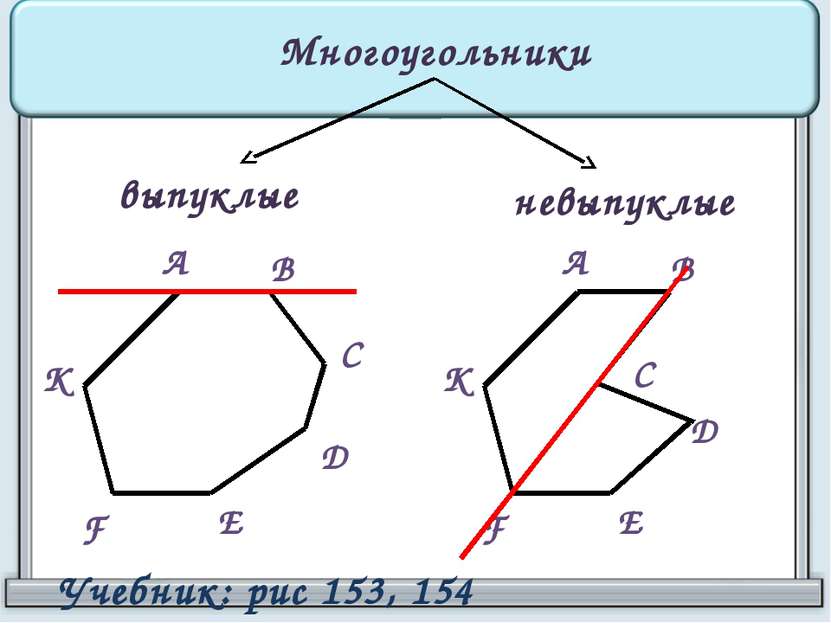
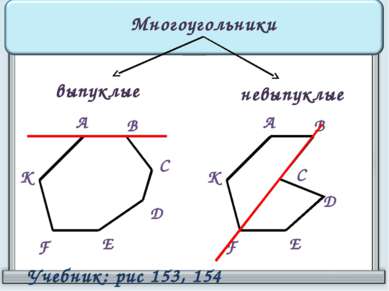
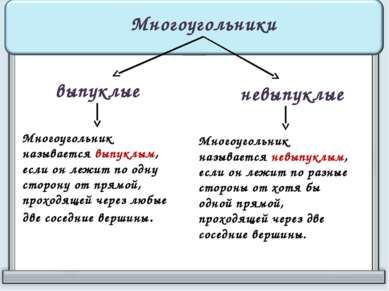Многоугольники выпуклые невыпуклые Многоугольник называется выпуклым, если он лежит по одну сторону от прямой, проходящей через любые две соседние вершины. Многоугольник называется невыпуклым, если он лежит по разные стороны от хотя бы одной прямой, проходящей через две соседние вершины.
Cлайд 10
Многоугольники выпуклые невыпуклые А В С D Е F К А В С D Е F К Учебник: рис 153, 154
Cлайд 11
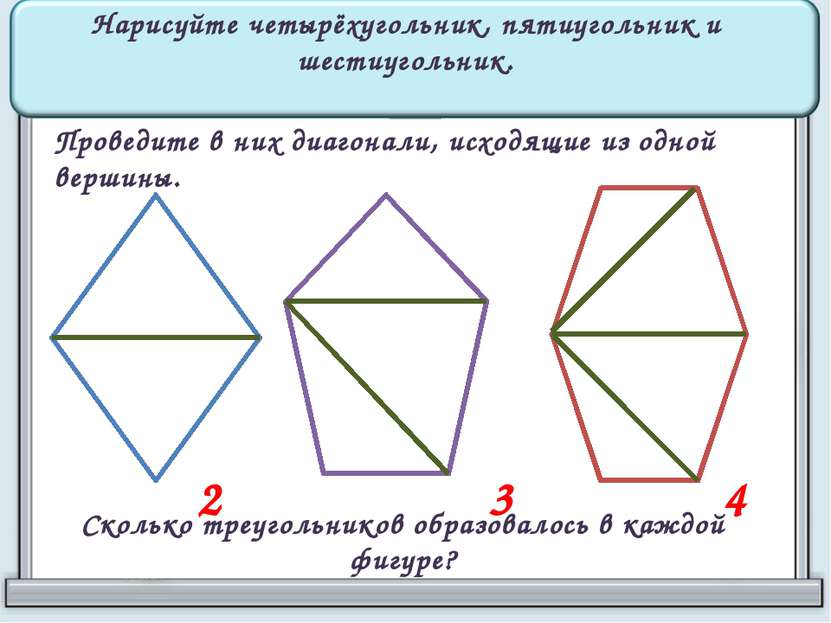
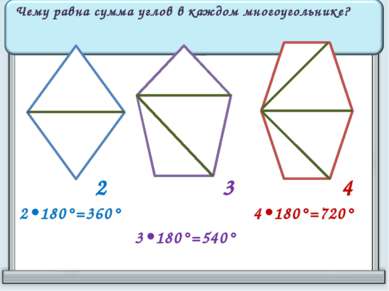
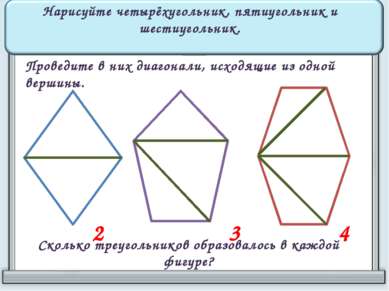Нарисуйте четырёхугольник, пятиугольник и шестиугольник. Проведите в них диагонали, исходящие из одной вершины. Сколько треугольников образовалось в каждой фигуре? 2 3 4
Cлайд 12
2 3 4 Чему равна сумма углов в каждом многоугольнике? 2•180°=360° 3•180°=540° 4•180°=720°
Cлайд 13
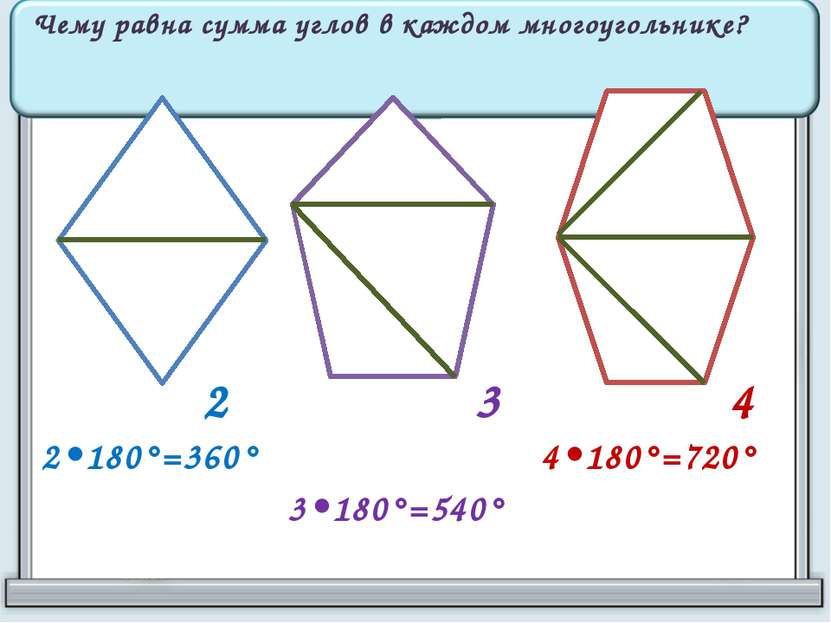
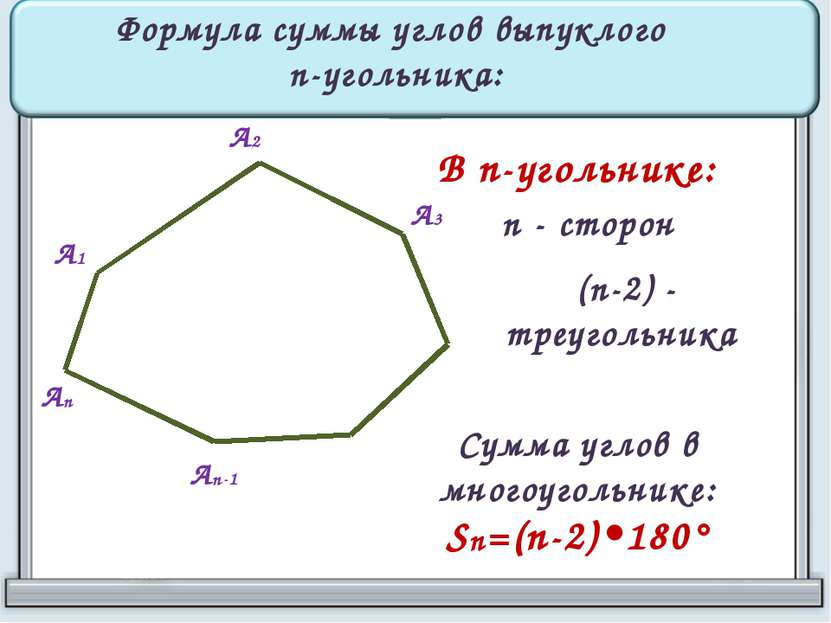
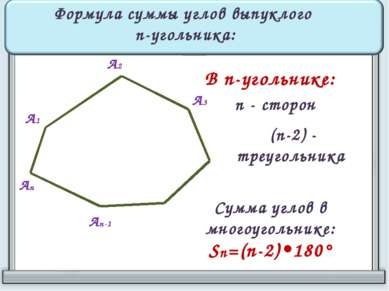А1 А2 А3 Аn-1 Аn Формула суммы углов выпуклого n-угольника: В n-угольнике: n - сторон (n-2) - треугольника Сумма углов в многоугольнике: Sn=(n-2)•180°
Cлайд 14
Выполните самостоятельно №364 из учебника S5=(5-2)•180°=3 •180°= 540° S6=(6-2)•180°=4 •180°= 720° S10=(10-2)•180°=8 •180°= 1440°
Cлайд 15
Домашнее задание: Учебник: п.39-41(пересказ) Вопросы 1-5 стр. 114 №366 МКОУ «СОШ №1 города Суздаля» Учитель математики: Плотникова Т.В.
