X
Код презентации скопируйте его
Решение систем неравенств (8 класс)
Скачать эту презентацию
Презентация на тему Решение систем неравенств (8 класс)
Скачать эту презентациюCлайд 1
Урок по алгебре в 8 классе по теме: «Решение систем неравенств» . Учитель математики ГБОУ СОШ № 322 Дубровская Т.И Санкт- Петербург 2012 г.
Cлайд 2
«Математика – наука о порядке» А. Уайтхед.
Cлайд 3
«Три пути ведут к знаниям: путь размышления- это путь самый благородный, путь подражания – это путь самый легкий и путь опыта- это путь самый горький». Конфуций. УМК к учебнику Ш. А. Алимова, Ю. М. Колягина и др. Тип урока: учебный практикум. Оборудование: магнитная доска, раздаточные таблицы, раздаточный дифференцированный материал для обучения и развития учащихся. Цели урока: 1. Систематизировать, расширить и углубить знания, умения учащихся применять различные способы решения систем неравенств и их комбинаций. 2. Уметь решать системы линейных неравенств и неравенств, сводящихся к линейным, извлекать необходимую информацию из учебно – научных текстов. 3. Знать о способах решения систем неравенств. 4. Способствовать развитию наблюдательности, умения анализировать, сравнивать, делать выводы. 5. Владеть навыками самоанализа, самоконтроля, побуждать учащихся к взаимоконтролю, вызывать у них потребность в обосновании своих высказываний.
Cлайд 4
Найти все решения системы неравенств и записать ответ с помощью числового промежутка: Ответ: Ответ: Ответ: Ответ: полуинтервал [- 3,7; 5,1) полуинтервал (3; 7,9] отрезок [-3,5; 2,7] луч (3; + ∞) Ответ: луч (- ∞;- 3,1] Ход урока: Организационный момент . Проверка домашнего задания ( фронтально). Дать ответы по домашнему заданию на вопросы учащихся. Блиц – опрос.
Cлайд 5
Алгоритм решения систем неравенств Чтобы решить систему неравенств, надо: 1) решить каждое неравенство системы; 2) изобразить решение каждого неравенства данной системы на одной числовой прямой. 3) записать решение системы, используя скобки, в случаях, когда решением является отрезок, луч, интервал или полуинтервал (решение может быть записано с помощью простейшего неравенства) 4) записать ответ IV. Напомним решение систем неравенств , для этого еще раз повторим алгоритм решения систем неравенств.
Cлайд 6
1) Решить систему неравенств: Решение. 1) решим каждое неравенство исходной системы, получим: : (−2) : 4 изобразим решение каждого из получившихся неравенств на ____________ числовой прямой: V. Выполнение упражнений.
Cлайд 7
\\\\\\\\\\\\\\\\\\ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ 1,5 -2 Ответ: (-2;1,5]. ,то есть
Cлайд 8
2) Решить систему неравенств: Решение. 1) Решим каждое из неравенств данной системы одновременно, получим: : 2, : 3, : 4; Изобразим решение каждого из получившихся неравенств на одной числовой прямой:
Cлайд 9
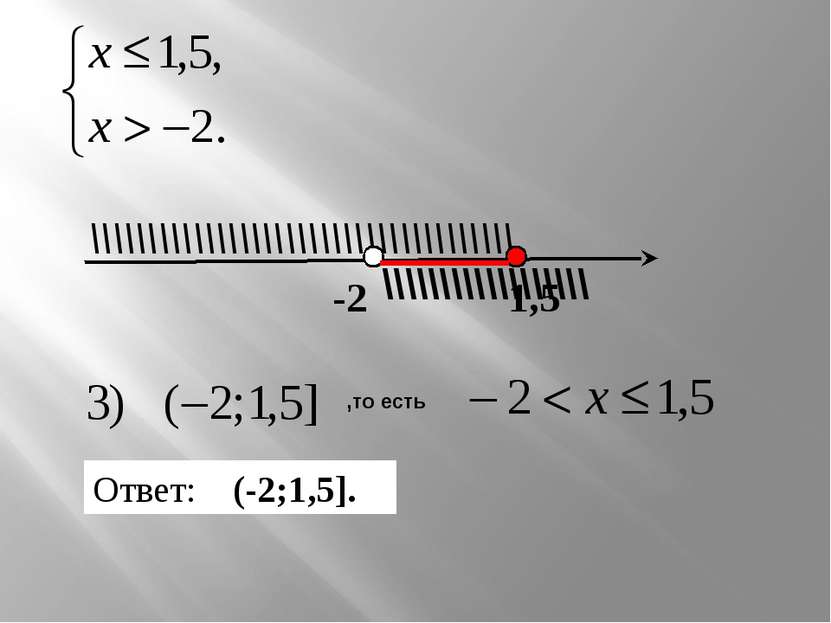
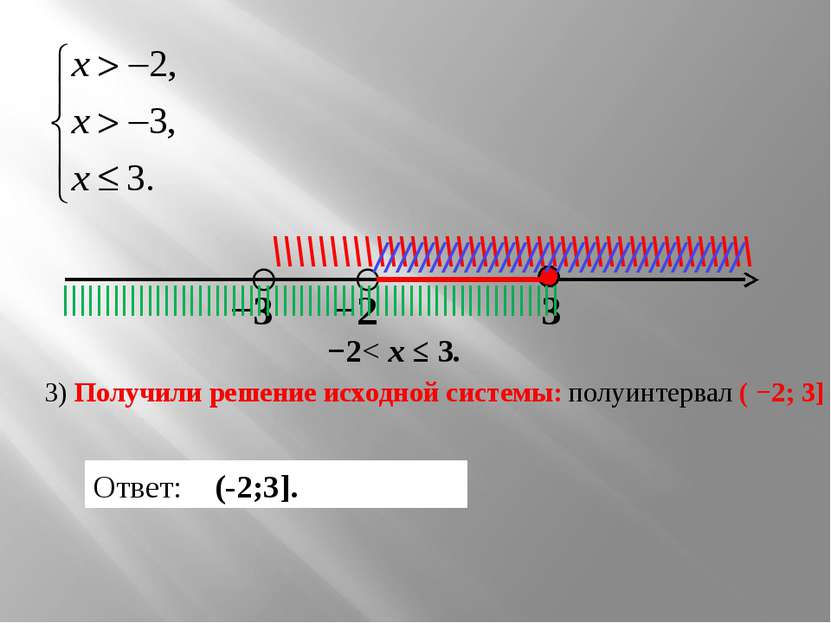
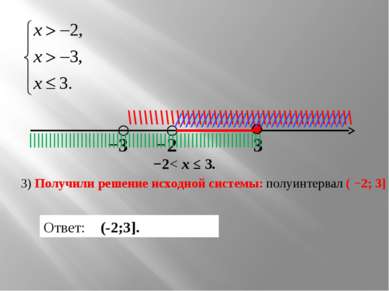−3 −2 3 ○ ○ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ //////////////////////////////// ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| 3) Получили решение исходной системы: полуинтервал ( −2; 3] Ответ: (-2;3]. −2< х ≤ 3.
Cлайд 10
3) Решить систему неравенств: Решение. 1) Решим каждое неравенство данной системы: : 2, : (−3);
Cлайд 11
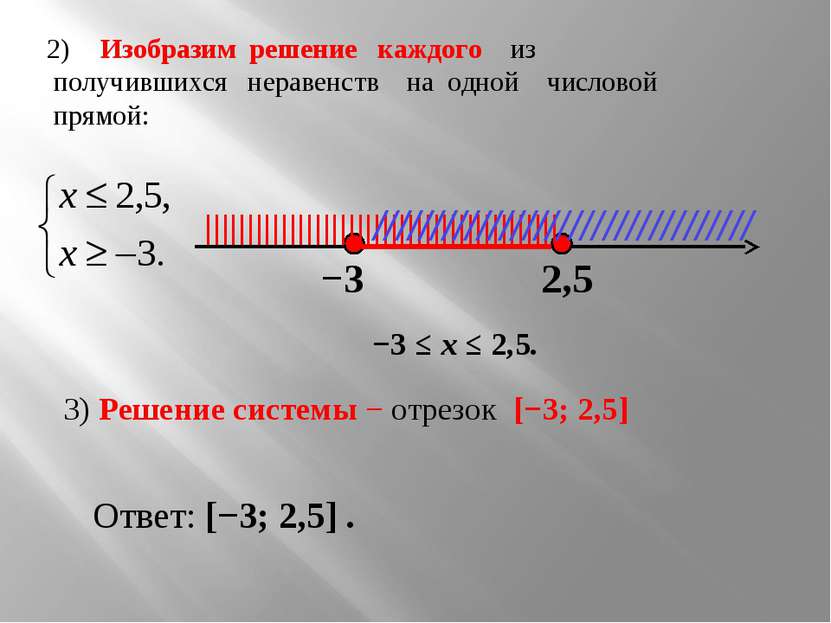
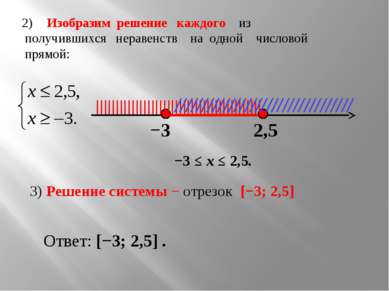Изобразим решение каждого из получившихся неравенств на одной числовой прямой: −3 2,5 |||||||||||||||||||||||||||||||||||||||||| ///////////////////////////////// 3) Решение системы − отрезок [−3; 2,5] Ответ: [−3; 2,5] . −3 ≤ х ≤ 2,5.
Cлайд 12
4) Подумай и реши. Выбери числовой промежуток, являющийся решением системы неравенств:
Cлайд 13
Выбери числовой промежуток, являющийся решением системы неравенств
Cлайд 14
Выбери наибольшее целое решение системы неравенств
Cлайд 15
Выбери наименьшее целое решение системы
Cлайд 16
5) Задача. Одна сторона треугольника равна 5 метрам, а другая- 8 метрам. Какой может быть третья сторона, если периметр треугольника больше 17 метров ? Решение. Пусть x метров (x>0) — длина третьей стороны треугольника, тогда, согласно условию задачи и учитывая неравенство треугольника, составим и решим систему неравенств: Ответ: длина третьей стороны больше 4 метров, но меньше 13 метров. 4 13 //////////////////////////////////////////////// \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ 4< х < 13, значит, длина третьей стороны есть любое число из интервала 4< х < 13.
Cлайд 17
VI. Итоги урока. Выставление оценок . Учащиеся умеют решать системы неравенств применяя различные способы их решения и научились показывать множество решений системы неравенств на координатной прямой. VII. Домашнее задание:§ 9. №№ 138 (2,4), 139 (2), 141 (4), 145.
