X
Код презентации скопируйте его
Решение систем неравенств (9 класс)
Скачать эту презентацию
Презентация на тему Решение систем неравенств (9 класс)
Скачать эту презентациюCлайд 1
Решение систем неравенств (9 класс) Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной
Cлайд 2
А. Нивен
Cлайд 3
Запомним Решить систему неравенств – это значит найти значение переменной, при котором верно каждое из неравенств системы.
Cлайд 4
Запомним Если надо решить систему неравенств, то: решаем каждое неравенство системы отдельно изображаем полученные решения на числовой прямой и смотрим пересечения этих решений. Эта общая часть и является решением данной системы неравенств.
Cлайд 5
Содержание Решение систем линейных неравенств Решение двойных неравенств Решение систем, содержащих квадратные неравенства
Cлайд 6
Решим систему неравенств (состоящую из линейных неравенств) 5х + 1 > 6 2х – 4 < 3 Решение: решим каждое неравенство отдельно 5х + 1 > 6 2х – 4 < 3 5х > 6 -1 2х < 4+3 5х > 5 2х < 7 х >1 х < 3,5 1 3,5 х Ответ: (1; 3,5)
Cлайд 7
Решим систему неравенств 5х + 12 ≤ 3х+ 20 х < 2х+3 2х + 7 ≥ 0 Решение: решим каждое неравенство отдельно 5х + 12 ≤ 3х+ 20 х < 2х+3 2х + 7 ≥ 0 5х – 3х ≤ - 12 + 20 х – 2х < 3 2х ≥ -7 2х ≤ 8 -х < 3 х ≥ -7/2 х ≤ 4 х > - 3 х ≥ -3,5 Изобразим на числовой прямой: -3,5 -3 4 Ответ: ( -3; 4]
Cлайд 8
Работа в парах: Решить систему неравенств: 1) 3х – 2 ≥ х + 1 4 – 2х ≤ х – 2 2) 3х > 12 + 11х 5х – 1 ≥ 0 Проверим ответы: 1) [2; +∞) 2) Нет решения
Cлайд 9
Примеры двойных неравенств Прочитайте неравенства: -6 < х < 0 -1,2 ≤ х < 3,5 0 < х ≤ 5,9
Cлайд 10
Решение двойных неравенств Решить неравенство: 0< 4х +2 ≤ 6 Решение: составим систему: 4х + 2 > 0 4х + 2 ≤ 6 Решим каждое неравенство системы отдельно: 1) 4х + 2 > 0 2) 4х + 2 ≤ 6 х > - 0,5 х ≤ 1 Полученные результаты изобразим на числовой прямой: -0,5 1 х Ответ: -0,5 < х ≤ 1 или (-0,5; 1]
Cлайд 11
Решите неравенства, работая в парах Решить неравенства: -6 ≤ - 3х ≤ 3 4 < 2х – 1 ≤ 13 -2 ≤ 6х + 7 < 1 0,3 < 0,5 + 0,1х < 0,6 0 < - 2х < 8 Проверим ответы: 1) [-1; 2] 2) (2,5; 7] 3) [- 1,5; - 1) 4) (-2; 1) 5) (-4; 0)
Cлайд 12
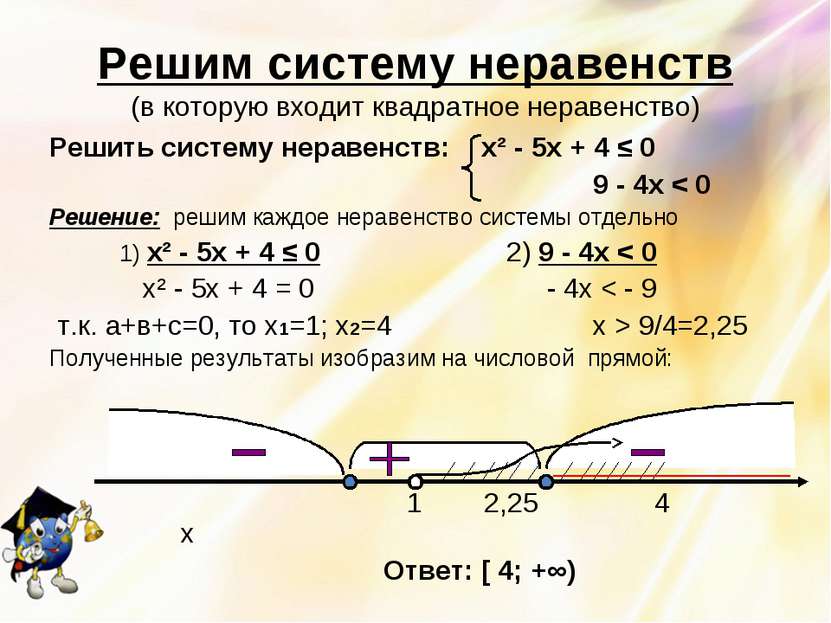
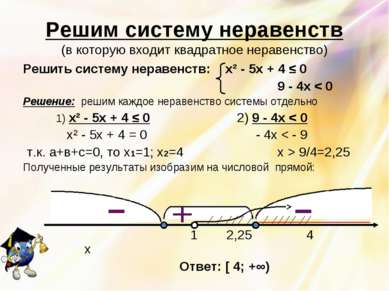Решим систему неравенств (в которую входит квадратное неравенство) Решить систему неравенств: х² - 5х + 4 ≤ 0 9 - 4х < 0 Решение: решим каждое неравенство системы отдельно 1) х² - 5х + 4 ≤ 0 2) 9 - 4х < 0 х² - 5х + 4 = 0 - 4х < - 9 т.к. а+в+с=0, то х1=1; х2=4 х > 9/4=2,25 Полученные результаты изобразим на числовой прямой: 1 2,25 4 х Ответ: [ 4; +∞)
Cлайд 13
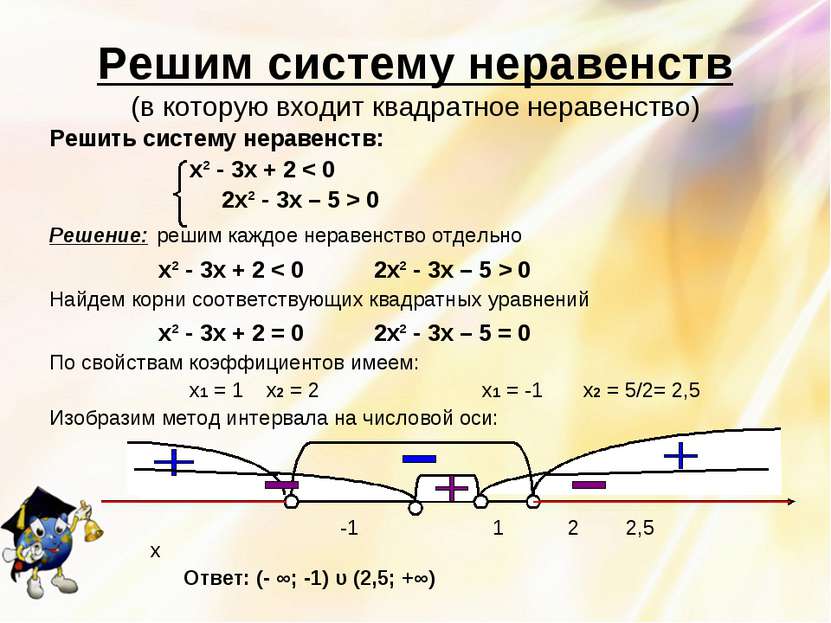
Решим систему неравенств (в которую входит квадратное неравенство) Решить систему неравенств: х² - 3х + 2 < 0 2х² - 3х – 5 > 0 Решение: решим каждое неравенство отдельно х² - 3х + 2 < 0 2х² - 3х – 5 > 0 Найдем корни соответствующих квадратных уравнений х² - 3х + 2 = 0 2х² - 3х – 5 = 0 По свойствам коэффициентов имеем: х1 = 1 х2 = 2 х1 = -1 х2 = 5/2= 2,5 Изобразим метод интервала на числовой оси: -1 1 2 2,5 х Ответ: (- ∞; -1) υ (2,5; +∞)
Cлайд 14
Решим системы неравенств, работая вместе 1) 6х² - 5х + 1 > 0 4х – 1 ≥ 0 2) 4х² - 1 ≤ 0 х² > 1 3х² - 2х – 1 < 0 х² - х – 6 > 0
Cлайд 15
Решите системы неравенств, работая самостоятельно 1) х² - 10х + 9 ≥ 0 12 – 3х < 0 2) 2х²- 5х + 2 > 0 4х – 1 ≥ 3 3) 2х² - 7х + 5 < 0 2 – х ≥ 0 Проверим ответы: 1) (4; 9] 2) [1; 2) 3) (- ∞; 1)
Cлайд 16
http://krasdo.ucoz.ru/ee383358c499.png
