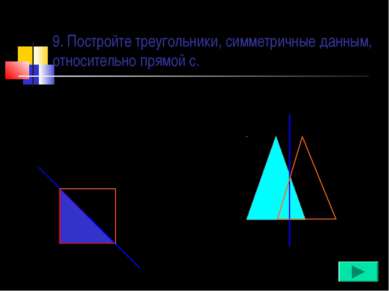
X
Код презентации скопируйте его
Осевая симметрия
Скачать эту презентацию
Презентация на тему Осевая симметрия
Скачать эту презентациюCлайд 1
Осевая симметрия Геометрия
Cлайд 2
Содержание Симметрия Осевая симметрия Задачи Симметрия в геометрии, природе, архитектуре, поэзии Заключение
Cлайд 3
Определение Симметрия (от греч. Symmetria – соразмерность), в широком смысле – неизменность структуры материального объекта относительно его преобразований. Симметрия играет огромную роль в искусстве и архитектуре. Но ее можно заметить и в музыке, и в поэзии. Симметрия широко встречается в природе, в особенности у кристаллов, у растений и животных. Симметрия может встретиться и в других разделах математики, например при построении графиков функций.
Cлайд 4
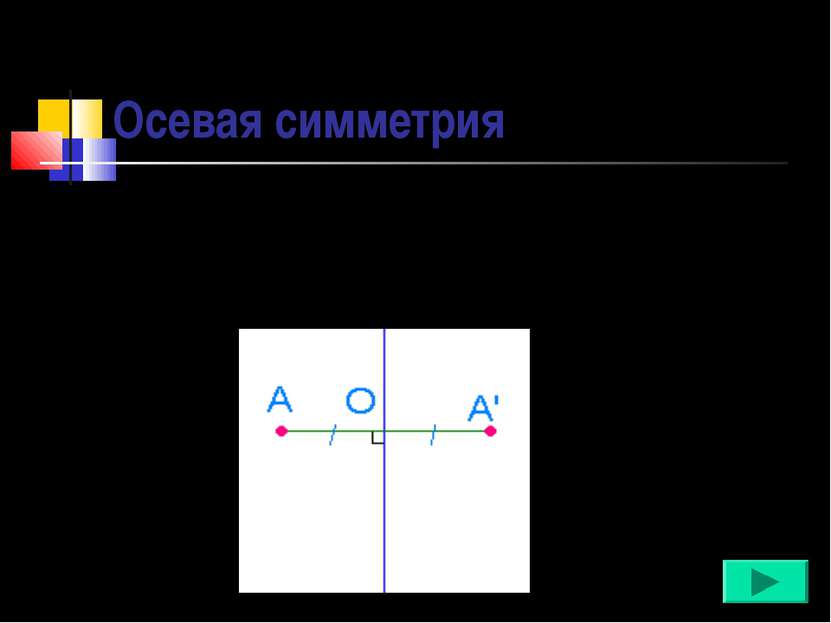
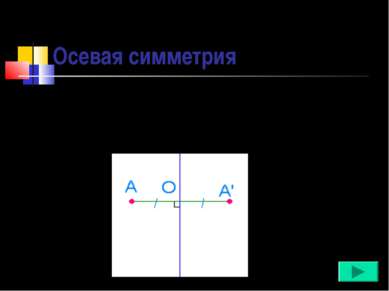Осевая симметрия Две точки, лежащие на одном перпендикуляре к данной прямой по разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно данной прямой.
Cлайд 5
Фигура называется симметричной относительно прямой a, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. а
Cлайд 6
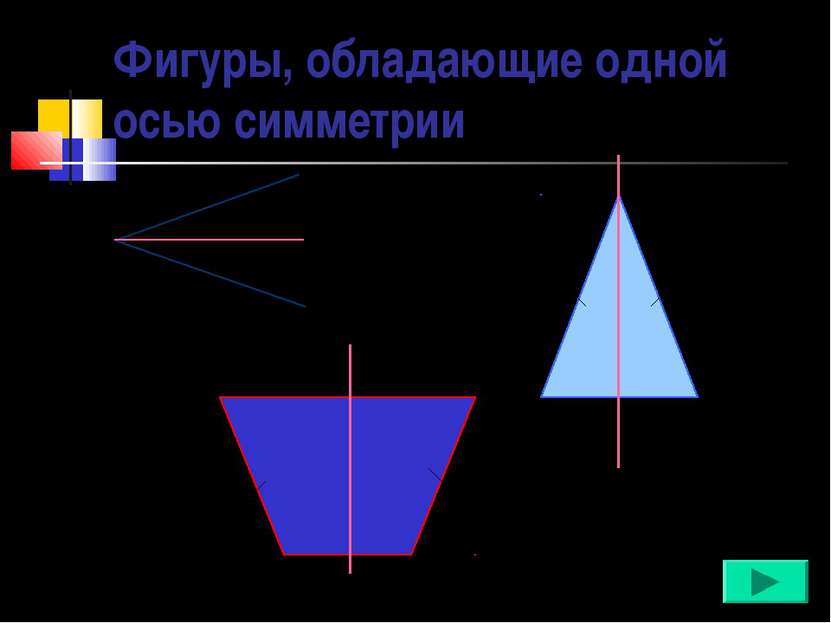
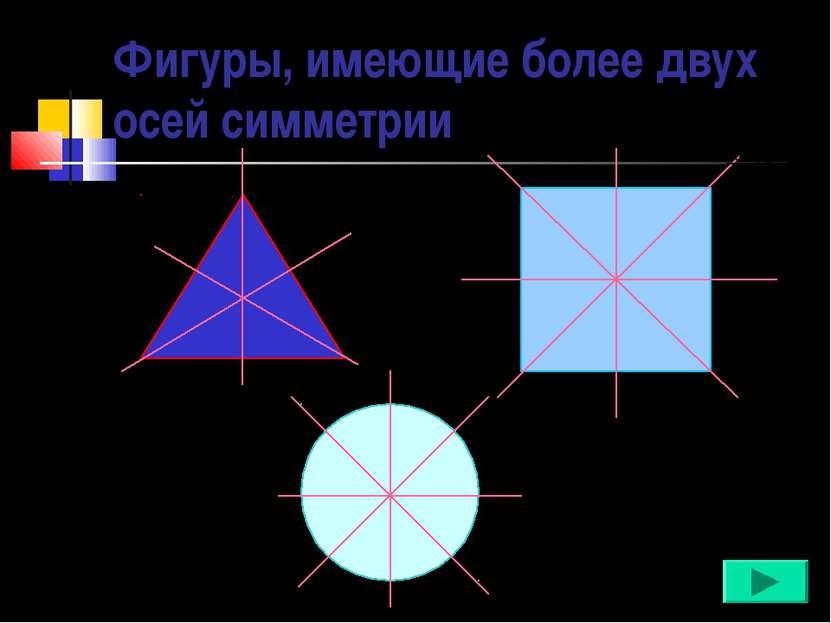
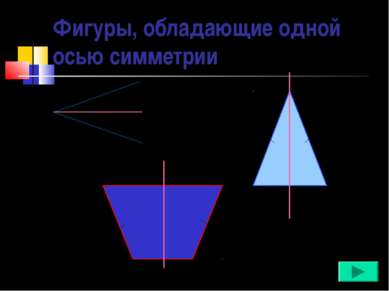Фигуры, обладающие одной осью симметрии Угол Равнобедренный треугольник Равнобедренная трапеция
Cлайд 7
Фигуры, обладающие двумя осями симметрии Прямоугольник Ромб
Cлайд 8
Фигуры, имеющие более двух осей симметрии Равносторонний треугольник Квадрат Круг
Cлайд 9
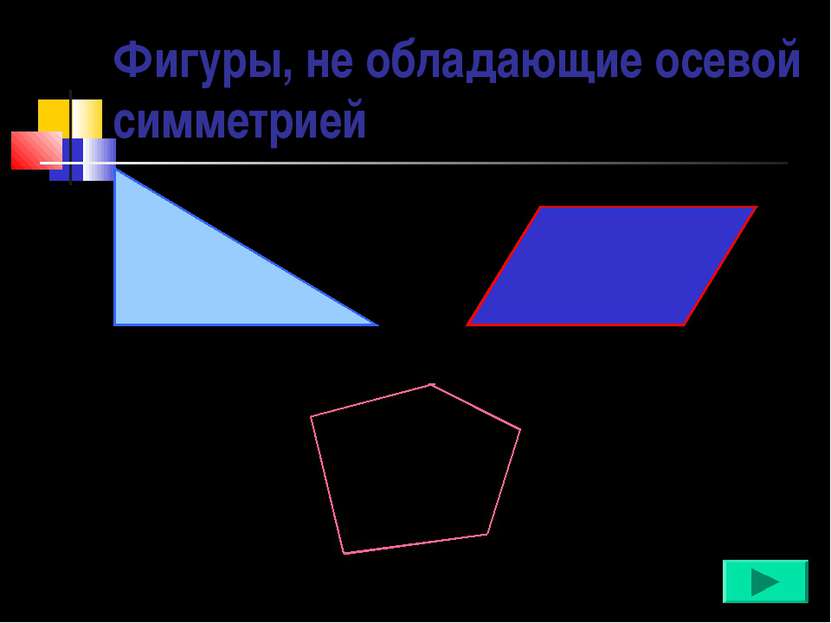
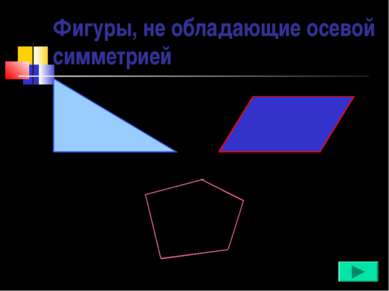Фигуры, не обладающие осевой симметрией Произвольный треугольник Параллелограмм Неправильный многоугольник
Cлайд 10
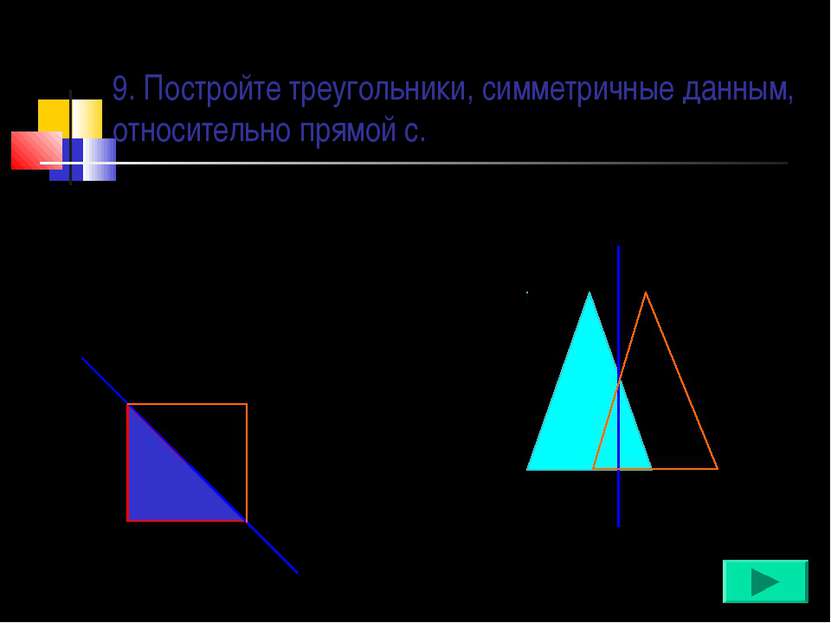
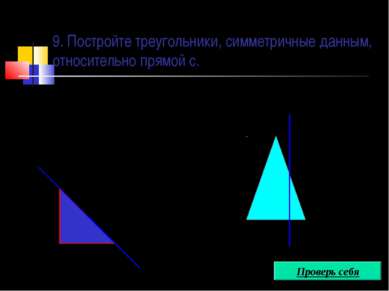
Построение точки, симметричной данной отрезка, симметричного данному треугольника, симметричного данному
Cлайд 11
Построение точки, симметричной данной А с А’ 1. АО с О 2. АО=ОА’
Cлайд 12
Построение отрезка, симметричного данному А с А’ В В’ O O' АА’ с, АО=ОА’. ВВ’ с, ВО’=О’В’. 3. А’В’ – искомый отрезок.
Cлайд 13
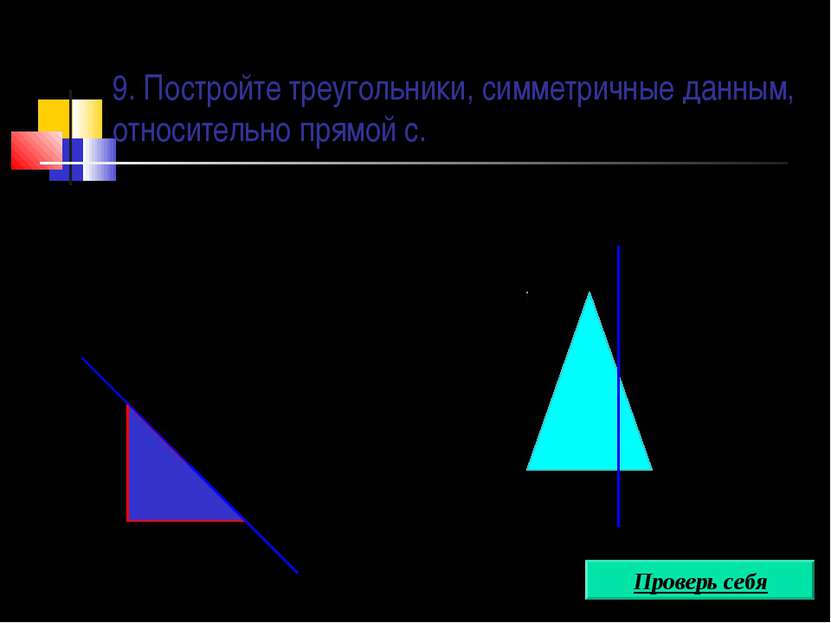
Построение треугольника, симметричного данному А с А’ В В’ С С’ 1. AA’ c AO=OA’ 2. BB’ c BO’=O’B’ 3. СС’ c СO”=O”С’ 4. A’B’С’ – искомый треугольник. O O” O’
Cлайд 14
1. Отрезок АВ, перпендикулярный прямой с, пересекает ее в точке О так, что АО≠ОВ. Симметричны ли точки А и В относительно прямой с? 2. Прямая а пересекает отрезок МК в его середине под углом, отличным от прямого. Симметричны ли точки М и К относительно прямой а? 3. Точки А и В расположены в различных полуплоскостях с границей р так, что отрезок АВ перпендикулярен прямой р и делится ею пополам. Симметричны ли точки А и В относительно прямой р? Задачи
Cлайд 15
4. Относительно какой из координатных осей симметричны точки М(7;2) и К(-7;2)? 5. Точки А(5;…) и В(…;2) симметричны относительно оси Ох. Запишите их пропущенные координаты. 6. Точка А(-2;3), В - симметричная ей точка относительно оси Ох, точка С – симметричная точке В относительно оси Оу. Найдите координаты точки С. 7. Точка А(3;1), В – симметричная ей точка относительно прямой у = х. Найдите координаты точки В. Задачи
Cлайд 16
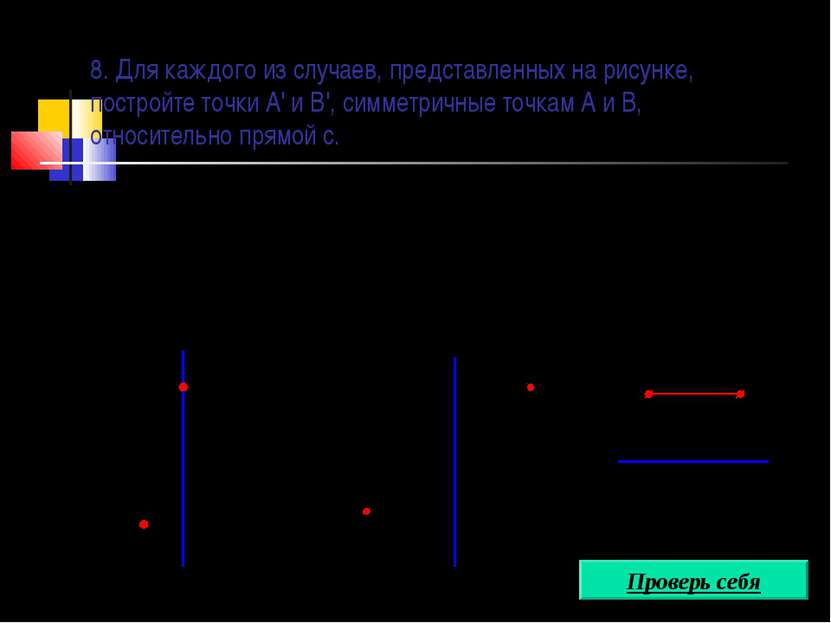
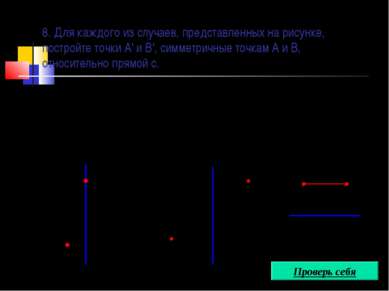8. Для каждого из случаев, представленных на рисунке, постройте точки А' и В', симметричные точкам А и В, относительно прямой с. В А с А В с А В с Проверь себя
Cлайд 17
8. Для каждого из случаев, представленных на рисунке, постройте точки А' и В', симметричные точкам А и В относительно прямой с. В В' А А' с А А' В В' с А В с А' В'
Cлайд 18
9. Постройте треугольники, симметричные данным, относительно прямой с. с с Проверь себя
Cлайд 19
9. Постройте треугольники, симметричные данным, относительно прямой с. с с
Cлайд 20
Симметрия в природе
Cлайд 21
В архитектуре
Cлайд 22
Симметрия в поэзии Пушкин А.С. «Медный всадник» …В гранит оделася Нева; Мосты повисли над водами; Темнозелеными садами Ее покрылись острова…
Cлайд 23
Заключение Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие народы с древнейших времен владели представлением о симметрии в широком смысле – как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство».
