X
Код презентации скопируйте его
Второй признак равенства треугольников
Скачать эту презентацию
Презентация на тему Второй признак равенства треугольников
Скачать эту презентациюCлайд 1
Автор: Галдин В. А. МБОУ ЛСОШ №3 п. Локоть Брасовского р-на Электронный адрес: galdin.vas@yandex.ru
Cлайд 2
Второй признак равенства треугольников 7 класс
Cлайд 3
Повторение: Равенство треугольников Два треугольника называются равными, если совмещаются наложением Первый признак равенства (по двум сторонам и углу между ними) Если две стороны и угол между ними одного треугольника соответственно равны сторонам и углу между ними другого треугольника, то такие треугольники равны
Cлайд 4
Теорема: Если сторона и два прилегающих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Cлайд 5
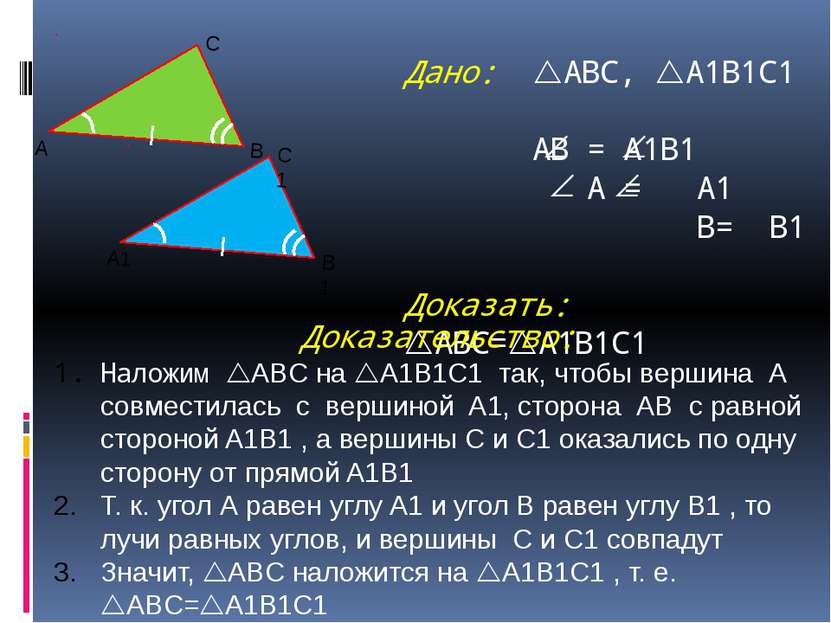
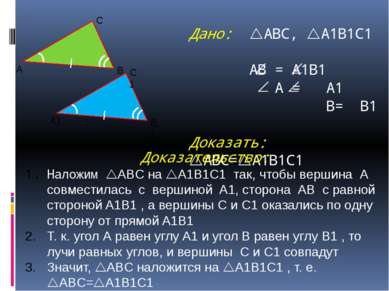Дано: ABC, A1B1C1 АВ = A1B1 A = A1 B= B1 Доказать: ABC= A1B1C1 Доказательство: Наложим ABC на A1B1C1 так, чтобы вершина А совместилась с вершиной A1, сторона АВ с равной стороной A1B1 , а вершины С и C1 оказались по одну сторону от прямой A1B1 Т. к. угол А равен углу A1 и угол В равен углу B1 , то лучи равных углов, и вершины C и C1 совпадут Значит, ABC наложится на A1B1C1 , т. е. ABC= A1B1C1 А1 В1 С1 А В С
Cлайд 6
Решение задач А В С D Доказать равенство AВС и CDA
Cлайд 7
Решение задач А В С D О Доказать равенство AOD и BОC 2) Найти ВС и СО, если ОD = 23 см и DA = 30 см
Cлайд 8
Решение задач Т С В Р О Доказать равенство ТСО и РВО 2) Найти ОС и ТС, если ОВ = 5 дм и ВР = 30 см
