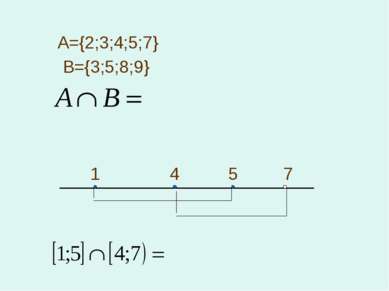Войти
X

Код презентации скопируйте его

Ширина px

Вы можете изменить размер презентации, указав свою ширину плеера!

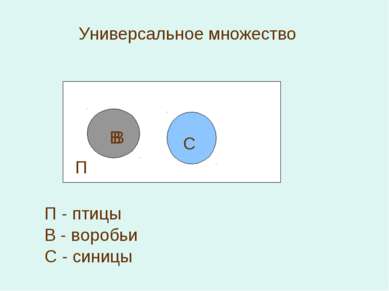
Множества

Скачать эту презентацию

Получить код Увеличить
Урок 4 Множества Множество есть многое, мыслимое нами как единое Георг Кантор Способы задания множеств: 1.Описание. Описание, включает основной, характерис... А Обозначения множеств {2, 3, 4, 5, 6, 7} круги Эйлера с b 2 5 [2;5] -3 7 [-3;7) Примеры Множество синиц Множество воробьев Универсальное множество П В В С П - птицы В - воробьи С - синицы Обозначение универсального множества I А А – подмножество I А включается в I Подмножество К Ч К - квадраты Ч - четырехугольники Добавляются еще характерис... Пустое множество Множество называется пустым, если в нем нет ни одного элемента Дополнение множества Дополнением множества А до I будет множество, состоящее ... Урок 5 Действия с множествами Действия с множествами 1.Объединением множеств А и В называется множество, со... А={2;3;4;5;7} B={3;5;8;9} 1 4 5 7 2. Пересечением множеств А и В называется множество, состоящее из элементов, ... А={2;3;4;5;7} B={3;5;8;9} 1 4 5 7 , , , Разностью множеств А и В называется множество, состоящее из элементов, ... Cр-1 Ф.И.
1 18

Презентация на тему Множества

Скачать эту презентацию

Cлайд 1
Урок 4 Множества Урок 4 Множества
Cлайд 2
Множество есть многое, мыслимое нами как единое Георг Кантор Множество есть многое, мыслимое нами как единое Георг Кантор
Cлайд 3
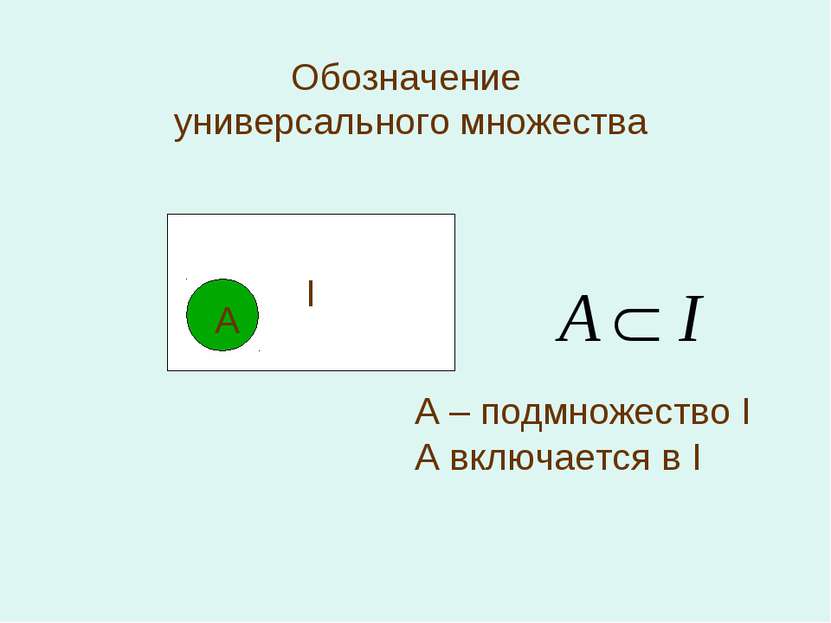
Способы задания множеств: 1.Описание. Описание, включает основной, характерис... Способы задания множеств: 1.Описание. Описание, включает основной, характеристический признак множества 2.Список Например, множество учеников нашего класса Бесконечные множества нельзя задавать списком
Cлайд 4
А Обозначения множеств {2, 3, 4, 5, 6, 7} круги Эйлера с b 2 5 [2;5] -3 7 [-3;7) А Обозначения множеств {2, 3, 4, 5, 6, 7} круги Эйлера с b 2 5 [2;5] -3 7 [-3;7)
Cлайд 5
Примеры Множество синиц Множество воробьев Примеры Множество синиц Множество воробьев
Cлайд 6
Универсальное множество П В В С П - птицы В - воробьи С - синицы Универсальное множество П В В С П - птицы В - воробьи С - синицы
Cлайд 7
Обозначение универсального множества I А А – подмножество I А включается в I Обозначение универсального множества I А А – подмножество I А включается в I
Cлайд 8
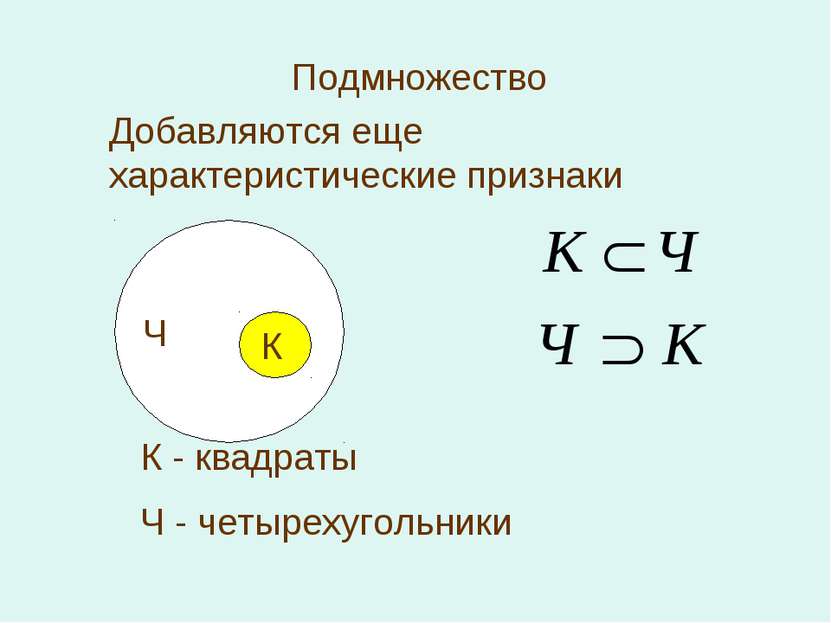
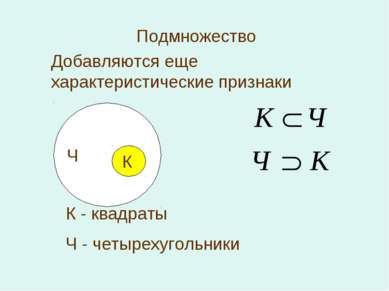Подмножество К Ч К - квадраты Ч - четырехугольники Добавляются еще характерис... Подмножество К Ч К - квадраты Ч - четырехугольники Добавляются еще характеристические признаки
Cлайд 9
Пустое множество Множество называется пустым, если в нем нет ни одного элемента Пустое множество Множество называется пустым, если в нем нет ни одного элемента
Cлайд 10
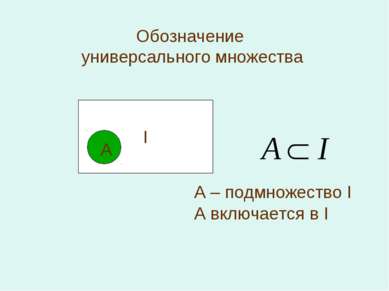
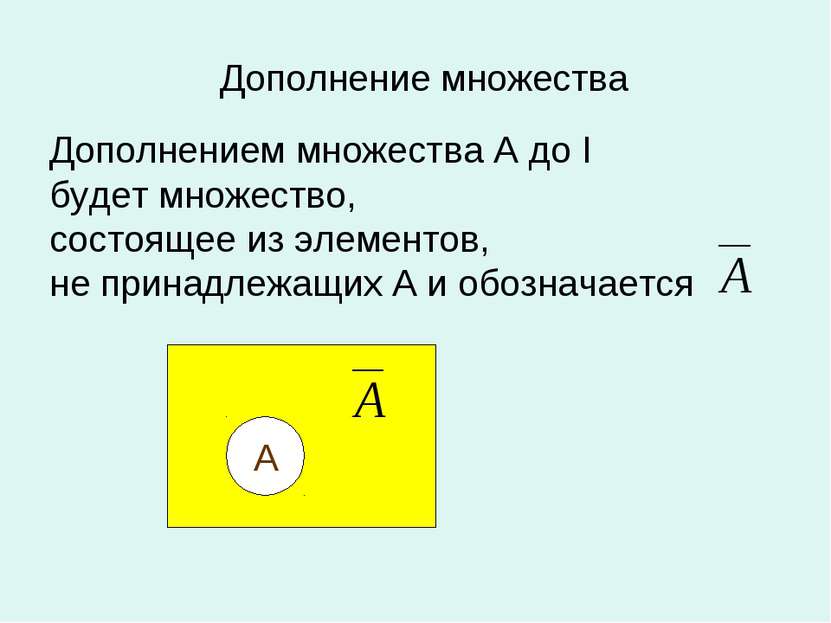
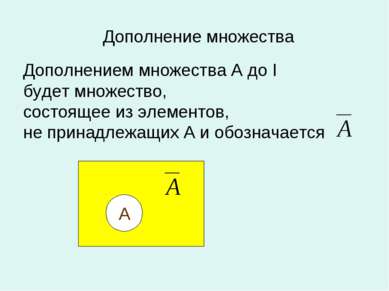Дополнение множества Дополнением множества А до I будет множество, состоящее ... Дополнение множества Дополнением множества А до I будет множество, состоящее из элементов, не принадлежащих А и обозначается А
Cлайд 11
Урок 5 Действия с множествами Урок 5 Действия с множествами
Cлайд 12
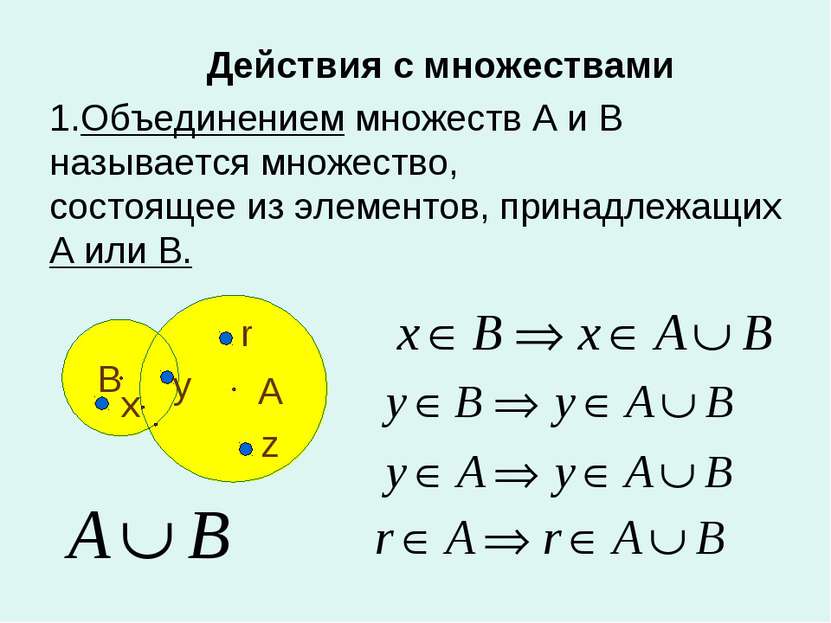
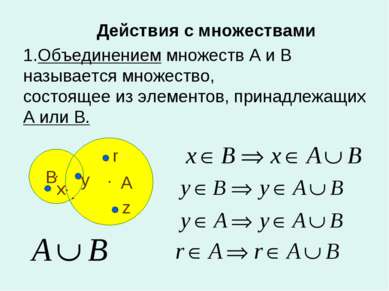Действия с множествами 1.Объединением множеств А и В называется множество, со... Действия с множествами 1.Объединением множеств А и В называется множество, состоящее из элементов, принадлежащих А или В. А В x y z r
Cлайд 13
А={2;3;4;5;7} B={3;5;8;9} 1 4 5 7 А={2;3;4;5;7} B={3;5;8;9} 1 4 5 7
Cлайд 14
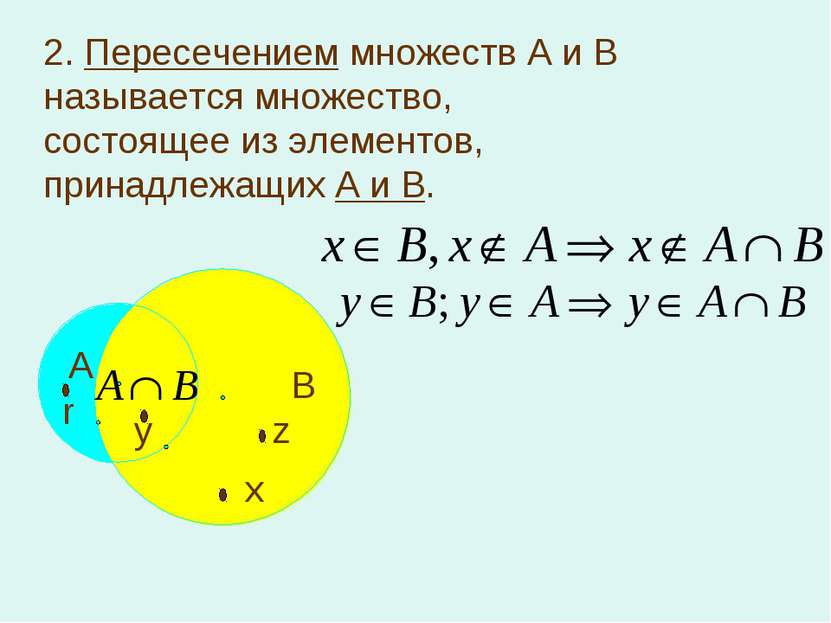
2. Пересечением множеств А и В называется множество, состоящее из элементов, ... 2. Пересечением множеств А и В называется множество, состоящее из элементов, принадлежащих А и В. A B x y r z
Cлайд 15
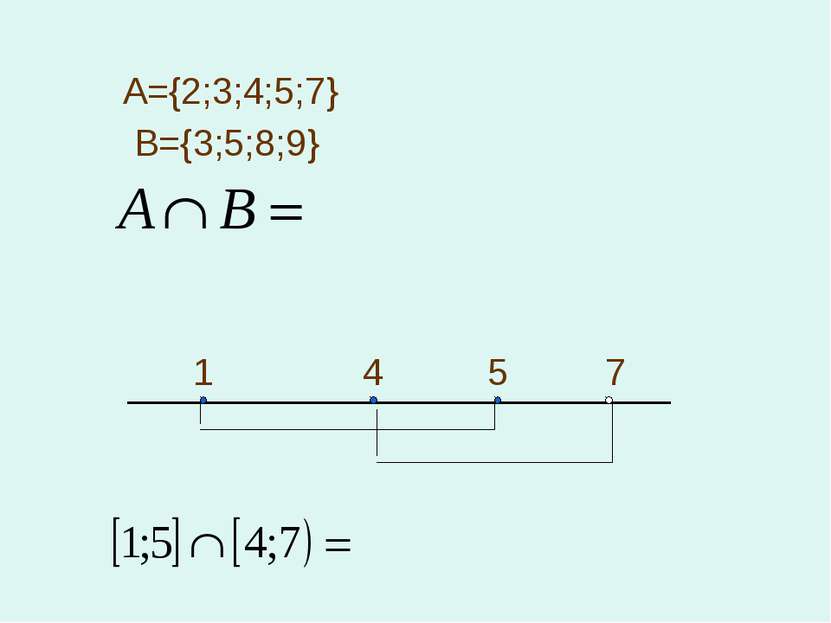
А={2;3;4;5;7} B={3;5;8;9} 1 4 5 7 А={2;3;4;5;7} B={3;5;8;9} 1 4 5 7
Cлайд 16
Cлайд 17
, , , Разностью множеств А и В называется множество, состоящее из элементов, ... , , , Разностью множеств А и В называется множество, состоящее из элементов, принадлежащих А, но не принадлежащих В если С= А\В и Неоднозначная операция если если
Cлайд 18
Cр-1 Ф.И. Cр-1 Ф.И.

Презентации этого автора

Скачать эту презентацию

Похожие презентаци


Поделится
Наверх