X
Код презентации скопируйте его
Решето Эратосфена
Скачать эту презентацию
Презентация на тему Решето Эратосфена
Скачать эту презентациюCлайд 1
Решето Эратосфена Презентация подготовлена учеником 6 А класса МОУ Гимназии №2 г. Железнодорожного Шарагиным Павлом
Cлайд 2
Решето Эратосфена - это алгоритм нахождения простых чисел до некоторого числа n. Простым называется число, которое можно разделить без остатка только на 1 и на само себя.
Cлайд 3
Алгоритм нахождения простых чисел Записать в ряд все числа от 2 до n 2 (первое число списка) – простое число. Обозначим его как p. Необходимо вычеркнуть из ряда все числа, делящиеся на р без остатка(2р, 3р, 4р и т.д) Возьмем следующее незачеркнутое число - 3, и теперь обозначим его как р. Снова вычеркнем числа, делящиеся на р без остатка. Будем повторять этот алгоритм до тех пор, пока р не станет больше, чем n. Все невычеркнутые числа в ряду – Простые.
Cлайд 4
Разберем алгоритм на примере. Шаг 1й Запишем ряд чисел от 2 до 50 ( n = 50) Первое простое число – 2 (р=2). Вычеркнем из ряда все числа, которые можно разделить на два. 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
Cлайд 5
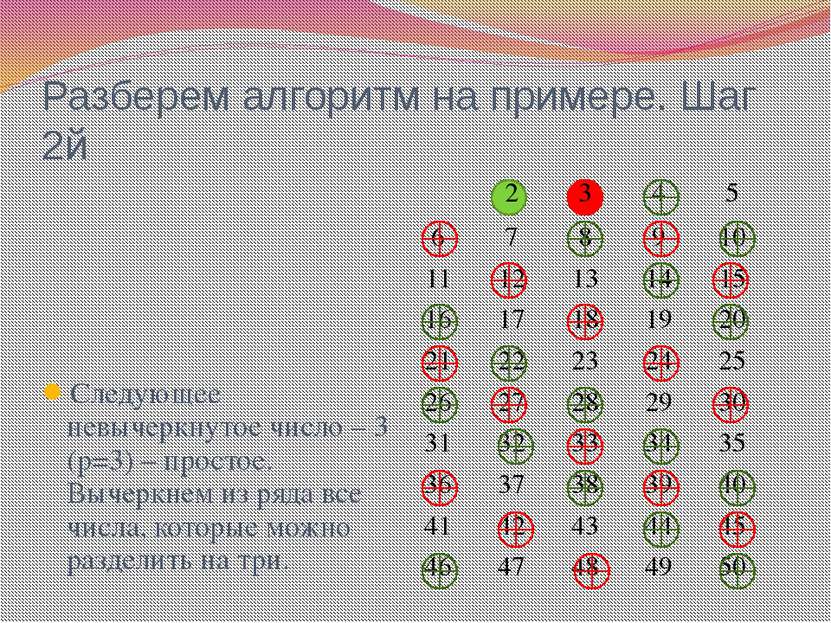
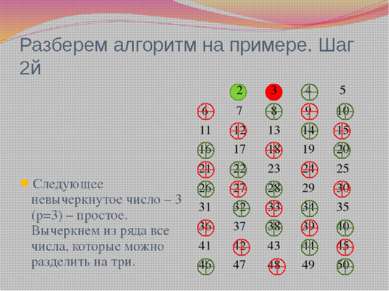Разберем алгоритм на примере. Шаг 2й Следующее невычеркнутое число – 3 (р=3) – простое. Вычеркнем из ряда все числа, которые можно разделить на три. 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
Cлайд 6
Разберем алгоритм на примере. Шаг 3й Следующее невычеркнутое число – 5 (р=5) – простое. Вычеркнем из ряда все числа, которые можно разделить на пять. 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
Cлайд 7
Разберем алгоритм на примере. Шаг 4й Продолжим выполнять алгоритм со всеми невычеркнутыми числами, оставшимися в ряду. Все незачеркнутые числа – простые. В нашем случае это 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
Cлайд 8
Спасибо за внимание!
