X
Код презентации скопируйте его
Решето Эратосфена
Скачать эту презентацию
Презентация на тему Решето Эратосфена
Скачать эту презентациюCлайд 1
МОУ «Лицей №17» Фестиваль «Портфолио» Автор: Шульгина Дарья ученица 7 б класса Руководитель: Зандер С.И. учитель математики Славгород, 2008
Cлайд 2
Тема: «Решето Эратосфена»
Cлайд 3
Идея возникновения проекта: Ещё на уроке я поняла что такое простые и составные числа, но меня заинтересовали вопросы «а такие ли они простые «простые числа»?», сколько их вообще существует и можно ли обнаружить способ их нахождения Мне была интересна и сама задача, и технология ИКТ, и сам продукт, т.е в виде чего будет представлена моя работа
Cлайд 4
Цель: Нахождение простых чисел через освоение метода «Решето Эратосфена», с последующим созданием медиапрезентации и её использования на уроках математики
Cлайд 5
Задачи: Собрать и изучить материал Применить понятия «кратные и делители числа» из предыдущего проекта Рассмотреть отдельные варианты таблиц: до 48, до 100, до 150, до 200 Открыть какие-либо закономерности и свойства в ряду чисел Обобщить полученные данные и сформулировать вывод
Cлайд 6
Актуальность: Когда на форзаце учебника мы обнаружили таблицу простых чисел, то решили для себя, что авторы учебника придают этим числам большое значение и значит тема «простые числа» актуальна. И действительно, простые числа являются как бы «кирпичиками» из которых «строятся» остальные натуральные числа И так как в настоящее время материал более наглядно представить можно с помощью компьютера, то решили применить ИКТ
Cлайд 7
Методы: Поисковый Метод (от частного к общему) Технология: Исследование
Cлайд 8
Новизна исследования: Использование проектной технологии Применение компьютера для нахождения простых чисел, применение эффекта анимации для показа определённой группы чисел
Cлайд 9
Объект исследования: Метод поимки «простых чисел» Предмет исследования: Простые, составные числа
Cлайд 10
Источники: Босова Л.Л. Информатика 6кл-Москва: БИНОМ,2007 Виленкин Н.Я. Математика 6кл-Москва: Просвещение,2002 Клименченко Д.В. Задачи по математике для любознательных-Москва: Просвещение,1992 Сост. Э-68 Савин А.П. Энциклопедический словарь юного математика-М.: Педагогика, 1989 Фотографии выполнены автором- Шульгиной Дашей, (панорамы на стенах лицея)
Cлайд 11
Практическое использование: На уроках математики при изучении тем: «разложение чисел на множители», «приведение дробей к общему знаменателю» Созданная таблица, красочно оформленная, поможет и другим учащимся разобраться в нахождении простых чисел
Cлайд 12
Гипотеза: Мы освоим метод «Решето Эратосфе на», но, вероятнее всего, не сможем найти самое большое простое число
Cлайд 13
Загадочные простые числа Со времен древних греков простые числа оказываются столь же привлекательными, сколь и неуловимыми. Математики постоянно испытывают разные способы их «поимки», но до сих пор единственным по-настоящему эффективным остаётся тот способ, который найден александрийским математиком и астрономом Эратосфеном. А этому методу уже около 2 тыс. лет! Этим же вопросом занимался и древнегреческий математик Эвклид
Cлайд 14
Интерес древних математиков к простым числам связан с тем, что любое число, либо простое, либо может быть представлено в виде произведения простых ЧИСЕЛ, Т.Е. ПРОСТЫЕ ЧИСЛА- это такие «кирпичики», из которых строятся остальные натуральные числа.
Cлайд 15
Почему решето? Так как греки делали записи на покрытых воском табличках или на натянутом папирусе, а числа не вычёркивали, а выкалывали иглой, то таблица в конце вычислений напоминала решето. Поэтому метод Эратосфена и называл ся «Решетом Эратосфена»: в этом решете «отсеиваются» простые числа от составных.
Cлайд 16
Определения Если одно целое число можно разделить на другое без остатка, то второе число называется делителем первого. Кратным натуральному числу а называют натуральное число, которое делится без остатка на а. Натуральное число называется простым, если оно имеет только два делителя: единицу и само это число. Натуральное число является составным, если оно имеет более двух делителей.
Cлайд 17
Произвольный способ нахождения простых чисел 1 2 3 4 5 6 7 8 9 10 4пр.ч. 11 12 13 14 15 16 17 18 19 20 4пр.ч. 21 22 23 24 25 26 27 28 29 30 2пр.ч. 31 32 33 34 35 36 37 38 39 40 2пр.ч. 41 42 43 44 45 46 47 48 49 50 3пр.ч. 51 52 53 54 55 56 57 58 59 60 2пр.ч.
Cлайд 18
В этом случае мы не можем найти закономерность обнаружения простых чисел, они встречаются неравномерно. Мы находим их «вручную» Это очень интересное свойство простых чисел, они отказываются подчиниться какой либо закономерности (для примера: чётные числа встречаются через одно число в ряду натуральных чисел; числа кратные 3 встречаются через два числа и т.д.). Поэтому мы и обратились к варианту, который называется «Решетом Эратосфена»
Cлайд 19
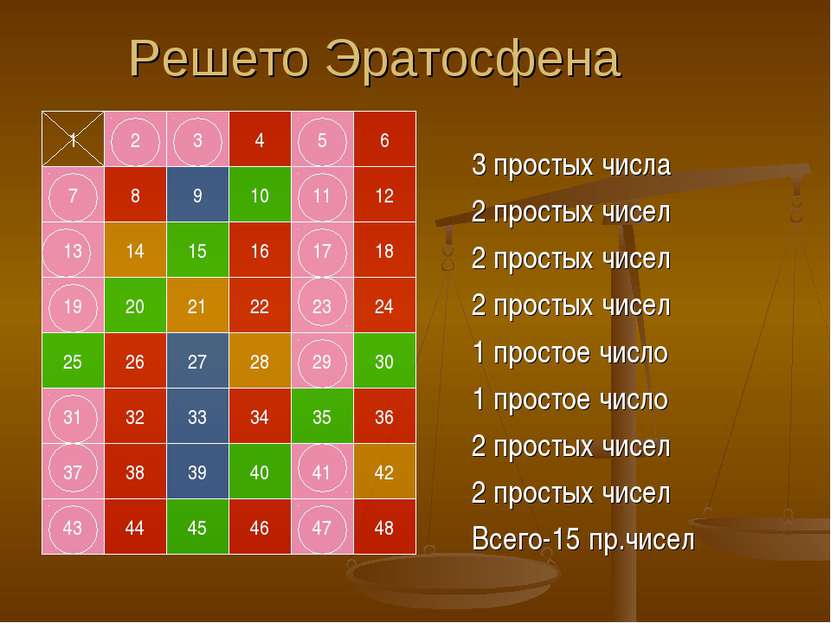
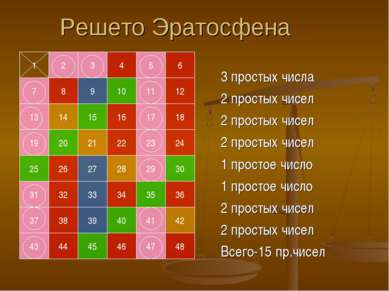1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 Решето Эратосфена 3 простых числа 2 простых чисел 2 простых чисел 2 простых чисел 1 простое число 1 простое число 2 простых чисел 2 простых чисел Всего-15 пр.чисел
Cлайд 20
Алгоритм нахождения простых чисел В этой таблице все простые числа, меньше 48 обведены кружками. Найдены они так. 1 имеет единственный делитель - себя, поэтому 1 не является простым числом, 2- наименьшее ( и единственное четное) простое число. Все остальные четные числа делятся на 2 и у них есть по крайней мере 3 делителя; поэтому могут быть вычеркнуты. Следующее не вычеркнутое число-3; оно имеет ровно 2 делителя, поэтому оно простое. Все остальные числа, кратные 3, вычеркиваются. Теперь первое не вычеркнутое число 5; оно простое, а все его кратные можно вычеркнуть. Продолжая вычеркивать кратные, можно отсеять все простые числа меньше 48.
Cлайд 21
А теперь найдем все простые числа меньше 100, для этого продолжим таблицу до 102, дополнительно определяя делится ли число на 2,3,5,7
Cлайд 22
49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 Таблица от 49 до 102 1 простое число 1 простое число 1 простое число 2 простых числа 1 простое число 2 простых числа 1 простое число 2 простых числа Всего-10 пр.чисел
Cлайд 23
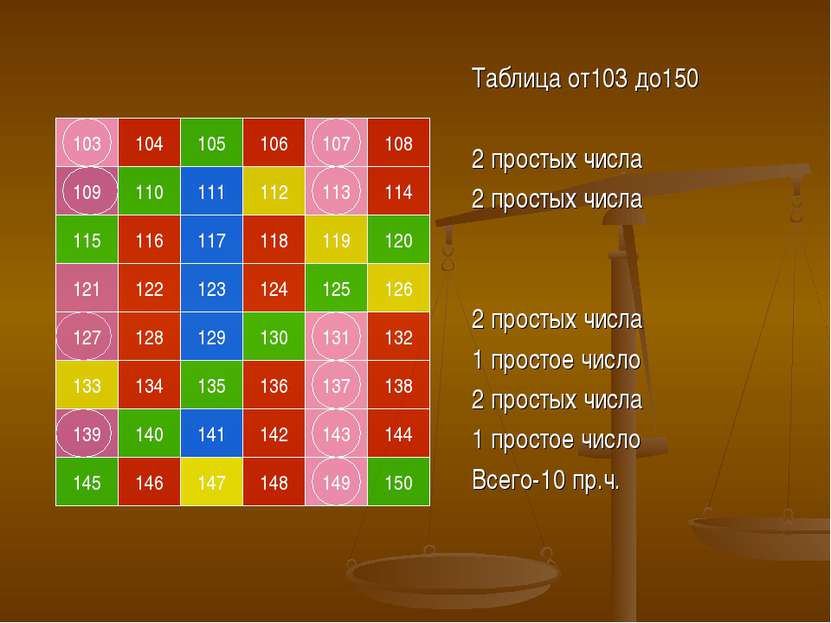
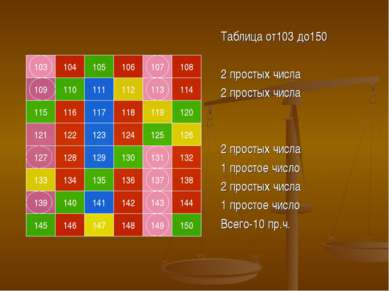103 105 104 107 106 108 109 111 110 113 112 114 115 117 116 119 118 120 121 123 122 125 124 126 127 129 128 131 130 132 133 135 134 137 136 138 139 141 140 143 142 144 145 147 146 149 148 150 Таблица от103 до150 2 простых числа 2 простых числа 2 простых числа 1 простое число 2 простых числа 1 простое число Всего-10 пр.ч.
Cлайд 24
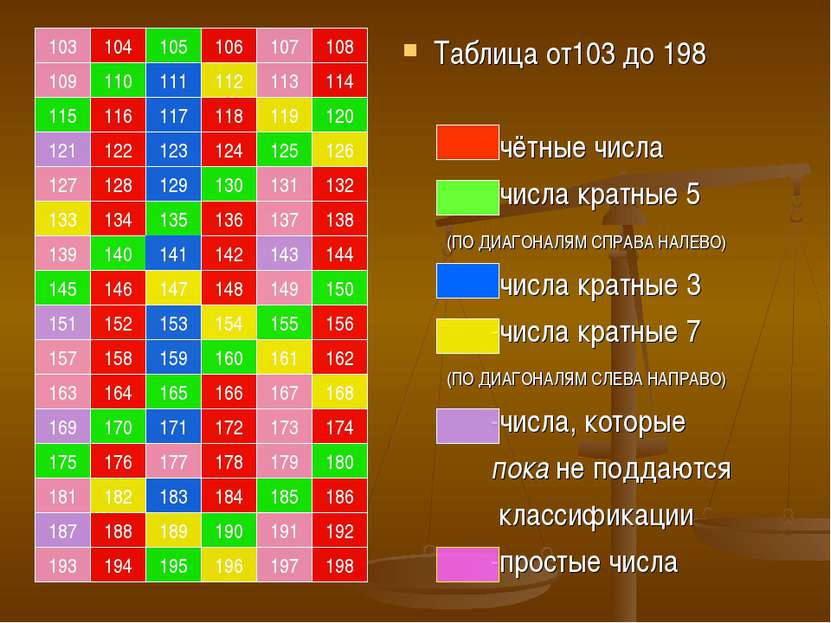
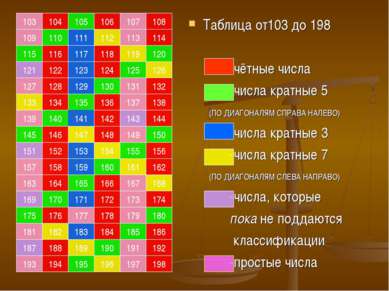105 103 104 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 Таблица от103 до 198 -чётные числа -числа кратные 5 (ПО ДИАГОНАЛЯМ СПРАВА НАЛЕВО) -числа кратные 3 -числа кратные 7 (ПО ДИАГОНАЛЯМ СЛЕВА НАПРАВО) -числа, которые пока не поддаются классификации -простые числа
Cлайд 25
Итак, простыми числами от 1 до 200 являются 25 чисел на первой сотне натуральных чисел: 2,3,5,7,11,13,17,19,23,29,31,37,41,43,4753,59,61,67,71,73,79,83,89,97 и 20 чисел на второй сотне: 101,103,107,109,113,127,131,137,139,149 157,163,167,173,179,181,191,193,197,199
Cлайд 26
Вывод Мы РАЗОБРАЛИСЬ, ЧТО ТАКОЕ ОПРЕДЕЛИТЕЛЬ ПРОСТЫХ ЧИСЕЛ («РЕШЕТО Эратосфена»), ПО ЕГО ПРИНЦИПУ СОЗДАЛИ СВОИ ТАБЛИЦЫ и нашли простые числа от 1 до 200, показали, что в одних рядах простых чисел больше, в других- меньше, т.е. встречаются они неравномерно. Но чем дальше мы продвигаемся по числовому ряду, тем реже встречаются простые числа. Возникает вопрос: а существует ли самое последнее простое число? Древнегреческий математик Евклид (IIIв. До н.э.) в своей книге «Начала», бывшей на протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т.е. за каждым простым числом есть ещё большее простое число. Наша гипотеза оказалась верна, указать самое большое простое число невозможно
Cлайд 27
Рефлексия Мне очень понравилось проводить исследования с простыми числами, которые «привлекательны», но в тоже время и неуловимы, я попыталась «уловить», отсеять простые числа от составных пользуясь «Решетом Эратосфена» т.е. проделала работу, которой 2 тыс. лет назад занимался александрийский математик Эратосфен. В дальнейшем я планирую создать таблицы, по которым можно будет проверять делится ли число на 11, 13, 17 и т.д.
Cлайд 28
