X
Код презентации скопируйте его
Комбинаторные задачи: перестановки
Скачать эту презентацию
Презентация на тему Комбинаторные задачи: перестановки
Скачать эту презентациюCлайд 1
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа №1 города Суздаля» Комбинаторные задачи: перестановки Факультативное занятие в 6 классе по теме: Учитель математики: Плотникова Т.В.
Cлайд 2
Вычислите : 10 2 Второй пример более сложный, поэтому его следует разобрать у доски.
Cлайд 3
Антон, Борис и Виктор купили 3 билета на футбол на 1-е, 2-е, 3-е места первого ряда стадиона. Сколькими способами мальчики могут занять эти места? Задача:
Cлайд 4
Решение задачи: А А А В Б Б Б В Может быть такая последовательность: А может быть и так: В В А Б Может быть и так: В В А А Б Б Ответ: 6 вариантов Заметим, что 3!=6
Cлайд 5
Теорема о перестановках элементов конечного множества: n различных элементов можно расставить по одному на n различных мест ровно n! способами. Перестановкой называется множество из n элементов, записанных в определённом порядке. Определение: Рn=n! Запомните!!! Введённое понятие и формулу учащимся следует записать в тетрадь.
Cлайд 6
Вычислите : 56 24
Cлайд 7
Вычислите : 116 1
Cлайд 8
2Рх =12 Решите уравнение : 4
Cлайд 9
Задача: Пять друзей решили сфотографироваться. Сколькими способами их можно рассадить? 120 Сколько фигурок можно сложить из Танграма? 7!
Cлайд 10
Найдите количество всех способов, которыми можно составить трехцветный флаг из горизонтальных полос красного, белого и синего цветов. Задача: А какие? Чтобы ответить на это вопрос давайте обозначим каждый цвет буквой, с которой он начинается: К – красный, Б – белый, С – синий. 6 Чтобы ответить на второй вопрос задачи, попросите ребят в тетрадях сделать соответствующие рисунки.
Cлайд 11
Задача: Сколько трёхзначных чисел можно получить, используя числа 1,2,3? Это числа: 123, 132, 213, 231, 312, 321 6 Сколько четырёхзначных чисел можно составить, используя числа 1,2,3,4? Заметили закономерность? 24
Cлайд 12
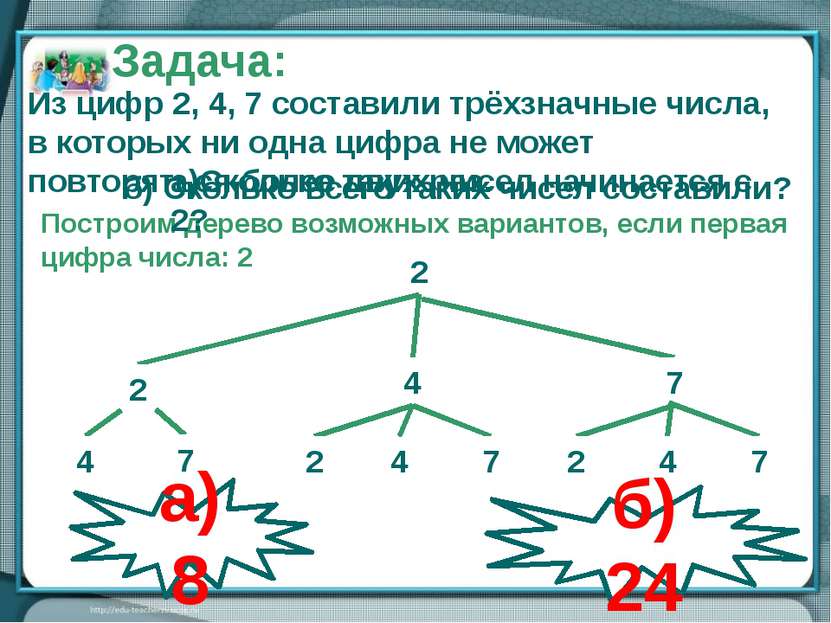
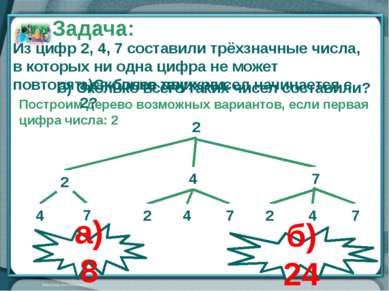2 4 2 7 4 7 2 7 2 7 4 4 Построим дерево возможных вариантов, если первая цифра числа: 2 Задача: Из цифр 2, 4, 7 составили трёхзначные числа, в которых ни одна цифра не может повторяться более двух раз. а) 8 б) 24 б) Сколько всего таких чисел составили? а)Сколько таких чисел начинается с 2?
Cлайд 13
247 274 224 227 242 272 244 Задача: Из цифр 2, 4, 7 составили трёхзначные числа. 2 б)Сколько таких чисел, в которых 2 может повторяться, начинаются с 2? 6 в)Сколько таких чисел, начинаются с двойки и цифра 4 может повторяться? 3 247 274 247 274 а)Сколько таких чисел, в которых ни одна цифра не может повторяться, начинаются с 2?
Cлайд 14
Расставляем предметы по порядку Математика 6 Литература 5 Русский язык 4 Английский язык 3 Биология 2 1 Физкультура Всего вариантов расписания 1•2•3•4•5•6=720 Задача: В 6 классе в среду 6 уроков: математика, литература, русский язык, английский язык, биология и физкультура. Сколько вариантов расписания можно составить? 720 Предмет Число вариантов
Cлайд 15
В 6 классе во вторник 5 уроков: физкультура, русский язык, литература, обществознание и математика. Сколько можно составить вариантов расписания на день, зная точно, что математика - последний урок? Ответ: 24 варианта Ответ: 24 варианта Задача: Чем отличается эта задача от предыдущей? Какой предмет можно не учитывать при составлении расписания? 4!=24
Cлайд 16
Имеется девять различных книг, четыре из которых - учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом ? Задача: 17280 Рассуждаем так: будем рассматривать учебники как одну книгу. Тогда на полке надо расставить не девять, а шесть книг. Это можно 6! способами. Учебники тоже можно менять местами. Это можно сделать 4! способами. Значит, число способов расположения книг на полке равно произведению 6! на 4!.
Cлайд 17
Проказница мартышка, Осел, Козел, Да косолапый мишка затеяли сыграть квартет…Вам знакомо это произведение? Задача: 4!=24 Какое отношение имеет эта басня к нашему уроку? Сформулируйте вопрос к задаче. Измените вопрос к задаче так, чтобы ответ был 3! Измените вопрос к задаче так, чтобы ответ был 2•3!
Cлайд 18
Р5 = 5! Задача: Петя, Вася, Галя, Света и Марина садятся на скамейку. Сколькими способами можно это сделать? 5!=120
Cлайд 19
Задача: Сколькими способами Петя, Вася, Галя, Света и Марина могут сесть так, чтобы Галя и Марина были рядом? 2•4!=48
Cлайд 20
Задача: Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Петя был в середине? 4!=24
Cлайд 21
Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Петя и Вася не были рядом? Задача: 72 Рассуждаем так: из общего количества пересаживаний ребят на скамейке(5!) вычитаем случаи, когда Петя и Вася сидят рядом(2•4!)
Cлайд 22
Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Света не была второй слева? Задача: 96 Рассуждаем так: из общего количества пересаживаний ребят на скамейке(5!) вычитаем случаи, когда Света сидит второй слева(4!)
Cлайд 23
Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Марина не сидела с краю? Задача: 72 Рассуждаем так: из общего количества пересаживаний ребят на скамейке(5!) вычитаем случаи, когда Марина сидит с левого края(4!) и когда она сидит с правого края(4!), т.е. 5!-2•4!
Cлайд 24
Сколькими способами Петю, Васю, Галю, Свету и Марину можно посадить так, чтобы Марина не была непосредственно между Галей и Светой? Задача: 108 Рассуждаем так: из общего количества пересаживаний ребят на скамейке(5!) вычитаем случаи, когда Марина сидит между Галей и Светой(3!) и когда она сидит между Светой и Галей(3!), т.е. 5!-2•3!
Cлайд 25
Сколькими способами можно переставить буквы в слове «эскиз»? Задача: 5!=120 Обратить внимание учащихся на то, что в данном слове нет повторяющихся букв.
Cлайд 26
Задача: Сколько слов можно получить, переставляя буквы в слове «переправа»? Чем отличается эта задача от предыдущей? Запишем следующую формулу: где к –сумма повторений различных букв, а к1,к2,… - повторения каждой различной буквы. Разберём эту формулу на нашем примере: Буква «п» встречается 2 раза, «е» – 2 раза, «р» – 2 раза, «а» – 2 раза, «в» – 1 раз, значит, к=2+2+2+2+1=9, к1=2,к2=2,к3=2,к4=3,к5=1. Подставим полученные значения в формулу: 22680
Cлайд 27
Сколько слов можно получить, переставляя буквы в словах: «молоко»? «математика»? Задача для самостоятельного решения: 120 1680
Cлайд 28
1. Весной мама покупает ребенку много фруктов. Она купила банан, яблоко, апельсин, лимон, грушу и киви. Найдите число возможных вариантов съедания фруктов. 2. Одиннадцать футболистов строятся перед началом матча. Первым становится капитан, вторым – вратарь, а остальные – случайным образом. Сколько существует способов построения? 3. Сколькими способами можно расставить на полке 10 книг, из которых 4 книги одного автора, а остальные – разных авторов, так, чтобы книги одного автора стояли рядом? Домашнее задание: Учащимся предлагается решить три задачи, а к одной из них на альбомном листе необходимо сделать рисунок.
Cлайд 29
До новых встреч с занимательными задачами
