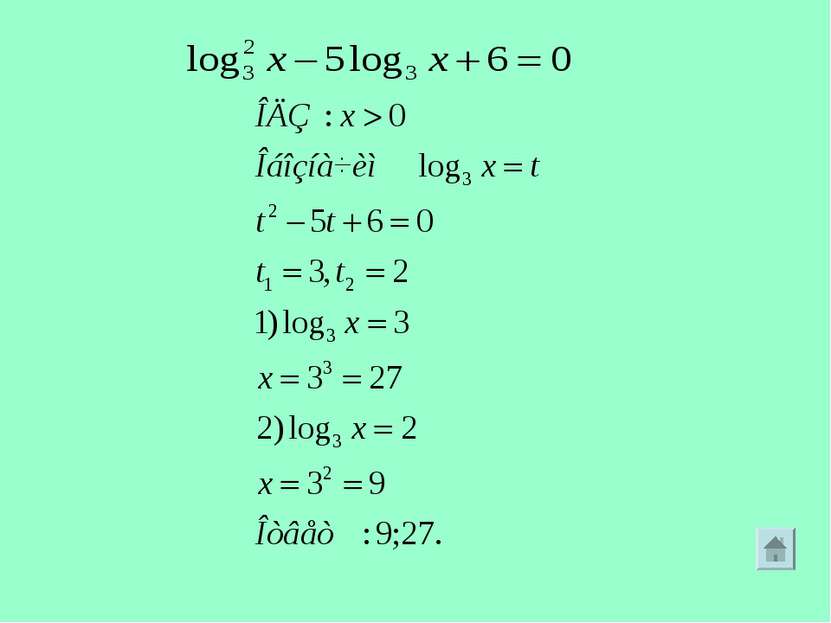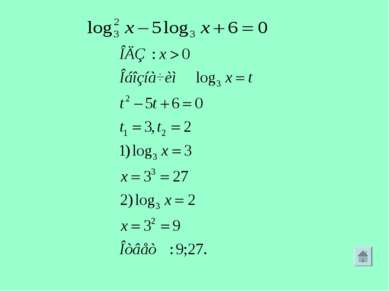X
Код презентации скопируйте его
Решение логарифмических уравнений
Скачать эту презентацию
Презентация на тему Решение логарифмических уравнений
Скачать эту презентациюCлайд 1
Решение логарифмических уравнений Урок изучения новой темы
Cлайд 2
Цель урока: обобщить материал по свойствам логарифмов, логарифмической функции; рассмотреть основные методы решения логарифмических уравнений; развивать навыки устной работы.
Cлайд 3
Вспомни и продолжи свойство!
Cлайд 4
Вычислите значения выражения
Cлайд 5
Вычислить значение выражения
Cлайд 6
Определение: Уравнения, содержащие неизвестное под знаком логарифма или в основании логарифма называются логарифмическими.
Cлайд 7
Методы решения ЛУ: Вид уравнения 1.Применение определения логарифма 2.Введение новой переменной 3. Приведение к одному и тому же основанию 4. Метод потенцирования 5 Метод логарифмирования обеих частей уравнения 6. Функционально-графический метод
Cлайд 8
Cлайд 9
Решение простейшего логарифмического уравнения основано на применении определения логарифма и решении равносильного уравнения Пример
Cлайд 10
Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их: если loga f(х) = loga g(х), то f(х) = g(х), решив полученное равенство, следует сделать проверку корней. Метод потенцирования
Cлайд 11
Cлайд 12
Если в уравнении содержатся логарифмы с разными основаниями, то прежде всего следует свести все логарифмы к одному основанию, используя формулы перехода
Cлайд 13
Если в показатели степени содержится логарифм, то обе части уравнения логарифмируют по тому основанию, которое содержится в основании логарифма, находящегося в показателе степени.
Cлайд 14
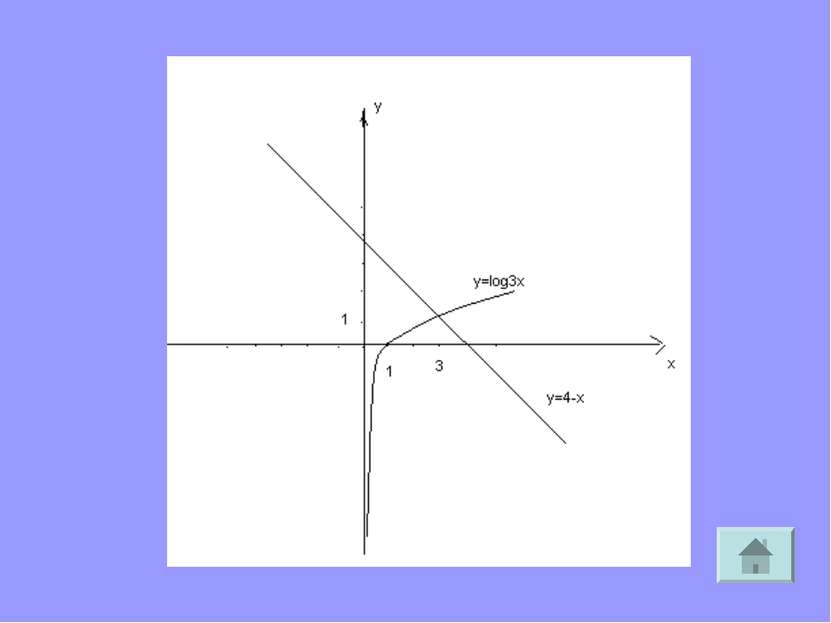
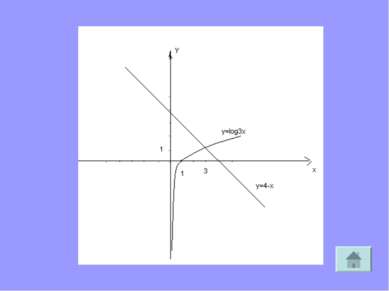
Для решения ЛУ графическим методом надо построить в одной и той же системе координат графики функций, стоящих в левой и правой частях уравнения и найти абсциссу их точки пересечения Пример log3 х = 4-х. Так как функция у= log3 х возрастающая, а функция у =4-х убывающая на (0; + ∞ ),то заданное уравнение на этом интервале имеет один корень.
Cлайд 15
Cлайд 16
Домашнее задание П.19,№337,338(четн.)
