X
Код презентации скопируйте его
Решение уравнений, содержащих модуль
Скачать эту презентацию
Презентация на тему Решение уравнений, содержащих модуль
Скачать эту презентациюCлайд 1
Цель: повторить , обобщить и систематизировать знания учащихся о модуле и его свойствах, умения решать различные уравнения , содержащие модуль. Учитель МОУ СОШ №6 г.Маркса Мартышова Л. И. Цель: повторить , обобщить и систематизировать знания учащихся о модуле и его свойствах, умения решать различные уравнения , содержащие модуль. Учитель МОУ СОШ №6 г.Маркса Мартышова Л. И. Цель: повторить , обобщить и систематизировать знания учащихся о модуле и его свойствах, умения решать различные уравнения , содержащие модуль. Учитель МОУ СОШ №6 г.Маркса Мартышова Л. И. Цель: повторить , обобщить и систематизировать знания учащихся о модуле и его свойствах, умения решать различные уравнения , содержащие модуль. Учитель МОУ СОШ №6 г.Маркса Мартышова Л. И.
Cлайд 2
Вид урока: урок – проект. Тип урока: обобщение и систематизация знаний с элементами исследования и организации проектной деятельности. Цели урока: Образовательные: обобщить и систематизировать знания учащихся о модуле и его свойствах; умения решать различные уравнения, содержащие модуль и уравнения, приводимые к уравнениям, содержащим модуль. Развивающие: развивать творческую и мыслительную деятельность учащихся, навыки проектно-исследовательской деятельности, способствовать формированию навыков коллективной работы, развивать умение чётко и ясно излагать свои мысли. Воспитательные: формирование интереса к предмету посредством вовлечения их в проектную деятельность, способствовать формированию навыков взаимодействия в малых группах.
Cлайд 3
Cлайд 4
Определение модуля Свойства модуля
Cлайд 5
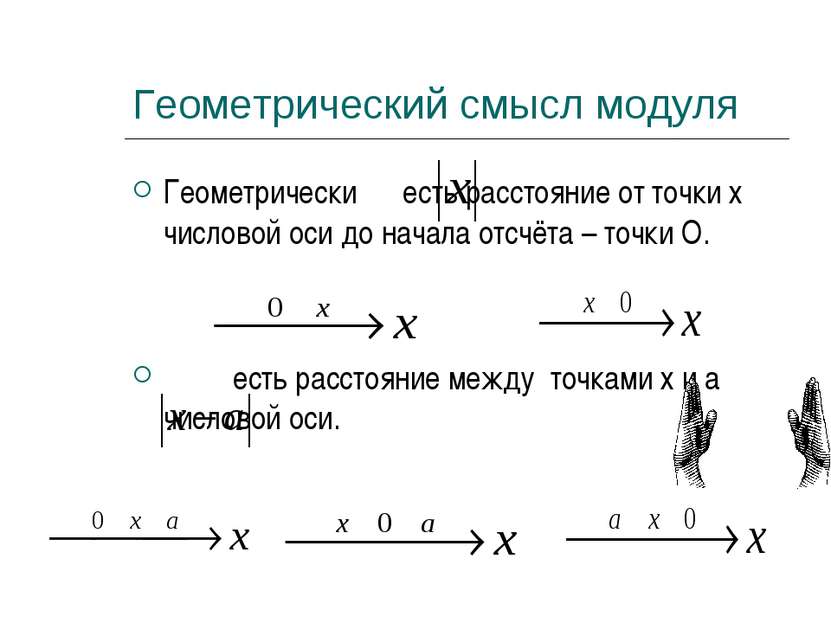
Геометрический смысл модуля Геометрически есть расстояние от точки х числовой оси до начала отсчёта – точки О. есть расстояние между точками х и а числовой оси.
Cлайд 6
Устная работа
Cлайд 7
Решите уравнения
Cлайд 8
Инструкция по работе над проектом. 1. Решить уравнения. 2. Проанализировать способы решения. 3. Провести классификацию данных уравнений: а) сгруппировать примеры по способам решения; б) определить, в чём заключается общий вид уравнений в каждой группе; в) дать название каждой группе уравнений. 4. Создать проект таблицы: « Решение уравнений, содержащих модуль». 5. Подготовить защиту проекта.
Cлайд 9
Защита проектов. . Оценочный лист. (5-бальная система) Владеет докладчик терминологией, которую использует в своём проекте Смог докладчик проекта доказать, что разработанная группой структура самая оптимальная для решения поставленной задачи Выполнила ли группа все поставленные перед ней задачи Творческие способности докладчика Оформление проекта
Cлайд 10
Простейшие уравнения вида ,b>0. По определению модуля 1. Ответ: -19;21.
Cлайд 11
Уравнения более общего вида Условие
Cлайд 12
Уравнения вида уравнение
Cлайд 13
Уравнения, приводимые к уравнениям, содержащим модуль. Иррациональное уравнение
Cлайд 14
Уравнения, приводимые к уравнениям, содержащим модуль Логарифмическое уравнение
Cлайд 15
Иррациональные уравнения, содержащие модуль. В силу того, что модуль раскрывается однозначно.
Cлайд 16
Cлайд 17
Иррациональные уравнения, содержащие модуль. В силу того, что модуль раскрывается двузначно. Ответ: -4,5; -0,75; 0.
Cлайд 18
Замена модуля.
Cлайд 19
Уравнения, содержащие несколько модулей. ( Решаемые с помощью метода интервалов) 1.Найдём значения х, при которых значения выражений, стоящих под знаком модуля, равны 0: х -1 = 0 при х = 1. х – 2=0 при х = 2. 2. Эти значения разбивают ОДЗ на промежутки: 3.Запишем на каждом из промежутков данное уравнение без знаков модуля. Получим совокупность систем.
Cлайд 20
Уравнение, содержащее несколько модулей. Метод интервалов
Cлайд 21
Cлайд 22
1.Простейшее уравнение, содержащее модуль, где b>0: 2.Уравнение более общего вида, содержащее модуль:
Cлайд 23
Уравнение вида По определению модуля
Cлайд 24
Уравнения, приводимые к уравнениям, содержащим модуль. 1
Cлайд 25
Уравнения, содержащие несколько модулей и те, которые не сводятся к виду │f(x) │= g(x) решаются с помощью метода интервалов: 1.Найдём значения x, при которых значение выражений, стоящих под знаком модуля, равны нулю. 2.Найденные значения x разбивают ОДЗ на промежутки. 3.Запишем на каждом из промежутков уравнение без знаков модуля. Получим совокупность систем.
Cлайд 26
Всего доброго, Вам!
